11-08 周三图解机器学习之实现逻辑异或，理解输出层误差和隐藏层误差项和动量因子-编程知识

11-08 周三图解机器学习之实现逻辑异或，理解输出层误差和隐藏层误差项

时间	版本	修改人	描述
2023年11月8日14:36:36	V0.1	宋全恒	新建文档

简介

最近笔者完成了《图解机器学习》这本书的阅读，由于最近深度学习网络大行其是，所以也想要好好的弄清楚神经网络的工作原理。比如说训练、比如说验证，比如说权重更新，之前也曾经写过两个博客来描述感知机和BP算法示意。

10-09 周一图解机器学习之深度学习感知机学习
11-06 周一神经网络之前向传播和反向传播代码实战

反向传播这个博客里主要通过一个样本，来不断的更新参数，但实际的神经网络结构是不会像博客中name简单的，因此还是需要给出一个计算公式的。在阅读图解机器学习P169页，如下代码时，自己没有看懂：

        # 计算输出层误差for k in range(self.no):error = targets[k] - self.ao[k]output_deltas[k] = dsigmoid(self.ao[k]) * error# 计算隐藏层的误差hidden_deltas = [0.0]*self.nhfor j in range(self.nh):error = 0for k in range(self.no):error = error + output_deltas[k] * self.wo[j][k]hidden_deltas[j] = dsigmoid(self.ah[j]) * error# 更新输出层权重for j in range(self.nh):for k in range(self.no):change = output_deltas[k]*self.ah[j]self.wo[j][k] = self.wo[j][k] + N*change + M * self.co[j][k]

上述在计算过程中求出了输出层误差和隐藏层误差项。如何理解这个代码片段呢？

完整代码

import math
import random
import string
random.seed(0)# 生成区间[a, b)内的随机数
def rand(a, b):return (b - a) *random.random() + a# 生成I*J大小的矩阵， 默认零矩阵
def makeMatrix(I, J, fill=0.0):m = []for i in range(I):m.append([fill]*J)return m# 函数 sigmoid， 采用tanh函数， 比起标准的1/(1+exp(-x))更好
def sigmoid(x):return math.tanh(x)# 函数sigmoid的派生函数 tanh(x)' = 1 - tanh(x)^2
def dsigmoid(x):return 1.0 - x**2class BPNeuralNet:'''建立三层反向传播神经网络'''def __init__(self, ni, nh, no) -> None:self.ni = ni + 1self.nh = nhself.no = no# 激活神经网络的所有节点self.ai = [1.0]* self.niself.ah = [1.0]*self.nhself.ao = [1.0]* self.no# 建立权重矩阵self.wi = makeMatrix(self.ni, self.nh)self.wo = makeMatrix(self.nh, self.no)# 设为随机值for i in range(self.ni):for j in range(self.nh):self.wi[i][j] = rand(-0.2, 0.2)for i in range(self.nh):for j in range(self.no):self.wo[i][j] = rand(-2.0, 2.0)# 建立动量因子self.ci = makeMatrix(self.ni, self.nh)self.co = makeMatrix(self.nh, self.no)# 前向传播，得到预计的输出。# 各个神经元的输出分别位于self.ah 和self.ao# inputs 代表一个样本def fp(self, inputs):if len(inputs) != self.ni -1:raise ValueError('与输入层节点数不符错误!')for i in range(self.ni-1):self.ai[i] = inputs[i]for j in range(self.nh):sum = 0.0for i in range(self.ni):sum += self.ai[i]* self.wi[i][j]self.ah[j] = sigmoid(sum)# 激活输出层for j in range(self.no):sum = 0for i in range(self.nh):sum += self.ah[i]*self.wo[i][j]self.ao[j] = sigmoid(sum)return self.ao[:]# N 学习速率 learning factor# M 动量因子 momentum factor# 基本思路是直接求出每个神经元的误差def back_propagate(self, targets, N, M):'''反向传播'''if len(targets) != self.no:raise ValueError("与输出层节点数不符!")output_deltas = [0.0] * self.no# 计算输出层误差for k in range(self.no):error = targets[k] - self.ao[k]output_deltas[k] = dsigmoid(self.ao[k]) * error# 计算隐藏层的误差hidden_deltas = [0.0]*self.nhfor j in range(self.nh):error = 0for k in range(self.no):error = error + output_deltas[k] * self.wo[j][k]hidden_deltas[j] = dsigmoid(self.ah[j]) * error# 更新输出层权重for j in range(self.nh):for k in range(self.no):change = output_deltas[k]*self.ah[j]self.wo[j][k] = self.wo[j][k] + N*change + M * self.co[j][k]self.co[j][k] = change# 更新输入层权重for i in range(self.ni):for j in range(self.nh):change=hidden_deltas[j]*self.ai[i]self.wi[i][j] += N * change + M * self.ci[i][j]self.ci[i][j] = changeerror = 0.0for k in range(len(targets)):error = error + 0.5*(targets[k]-self.ao[k])**2return errordef test(self, patterns):for p in patterns:print(p[0], '->', self.fp(p[0]))def weights(self):print('输入层权重')for i in range(self.ni):print(self.wi[i])print()print("输出层权重")for j in range(self.nh):print(self.wo[j])def train(self, patterns, iterations=100000, N =0.5, M=0.1):for i in range(iterations):error = 0.0for p in patterns:inputs = p[0]targets = p[1]self.fp(inputs)error = error + self.back_propagate(targets, N, M)if i % 100 ==0:print('计算误差的值是: %-.5f'%error)def trainprog():# BP神经网络学习逻辑异或pat = [[[0, 0], [0]],[[0, 1], [1]],[[1, 0], [1]],[[1, 1], [0]]]# 创建一个神经网络，输入层两个节点， 输出层两个节点，输出层一个节点：net = BPNeuralNet(2, 3, 1)net.train(pat)# 测试训练的成果net.test(pat)if __name__ == '__main__':trainprog()

上述代码在理解上并不复杂，主要是通过三层神经网络来拟合逻辑异或运算。采用的是个案更新的策略来更新权重参数。

权重更新

基础知识

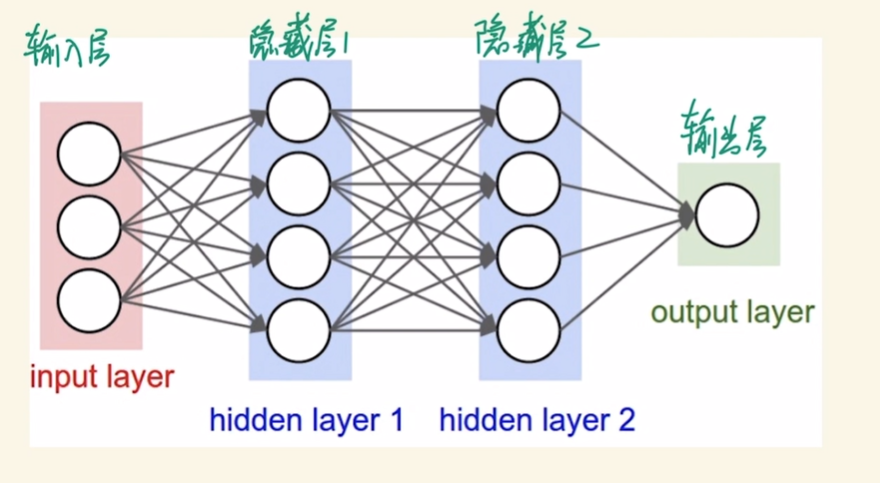
多层前馈神经网络。

一个示例：奶酪是否喜爱。

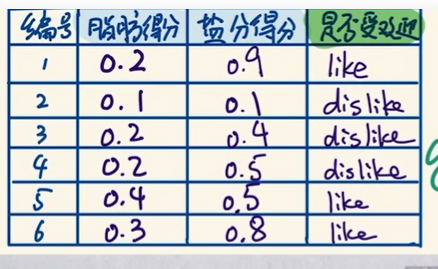
为此我们构建一个神经网络：

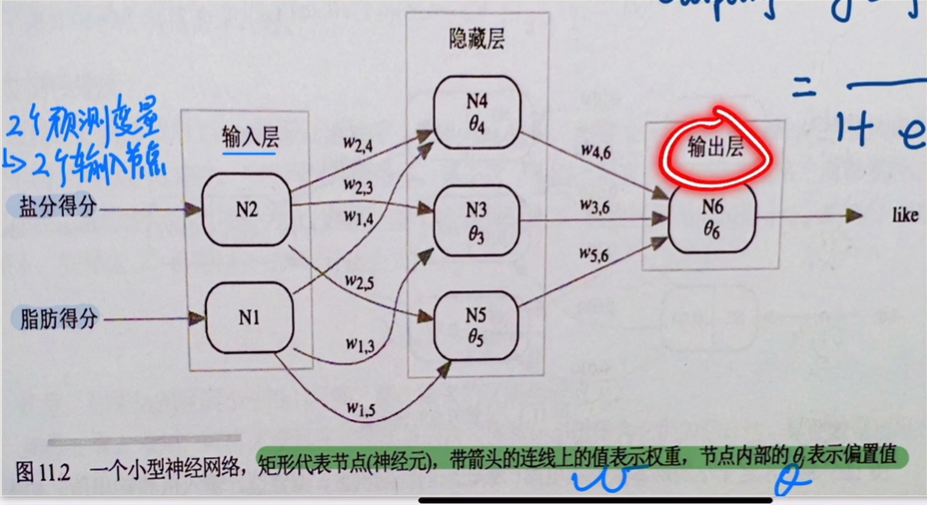
激活函数

指数函数
sigmoid
逻辑回归

校正因子的概念如下：

权重更新的策略有多种：

个案更新 case-based 更容易得到准确的结果。
批量更新 batch 优点就是比较快，加速。

迭代终止条件

迭代终止条件：

当权重和偏置差异与上一次非常小
误差达到之前设置的阈值
运行次数

存疑代码

        # 计算输出层误差for k in range(self.no):error = targets[k] - self.ao[k]output_deltas[k] = dsigmoid(self.ao[k]) * error# 计算隐藏层的误差hidden_deltas = [0.0]*self.nhfor j in range(self.nh):error = 0for k in range(self.no):error = error + output_deltas[k] * self.wo[j][k]hidden_deltas[j] = dsigmoid(self.ah[j]) * error# 更新输出层权重for j in range(self.nh):for k in range(self.no):change = output_deltas[k]*self.ah[j]self.wo[j][k] = self.wo[j][k] + N*change + M * self.co[j][k]self.co[j][k] = change# 更新输入层权重for i in range(self.ni):for j in range(self.nh):change=hidden_deltas[j]*self.ai[i]self.wi[i][j] += N * change + M * self.ci[i][j]self.ci[i][j] = change

上述分别计算出了输出层的误差项和输出层的误差项。按照上述代码理解，前两个for循环用于计算误差项，后两个循环用来更新权重，顺序从后向前，这也是反向传播得名的由来。关键是为什么输出层的误差是这么得来的呢？

参考 BP神经网络-第6集反向传播误差，调整全部权重，这对于理解是非常关键的。

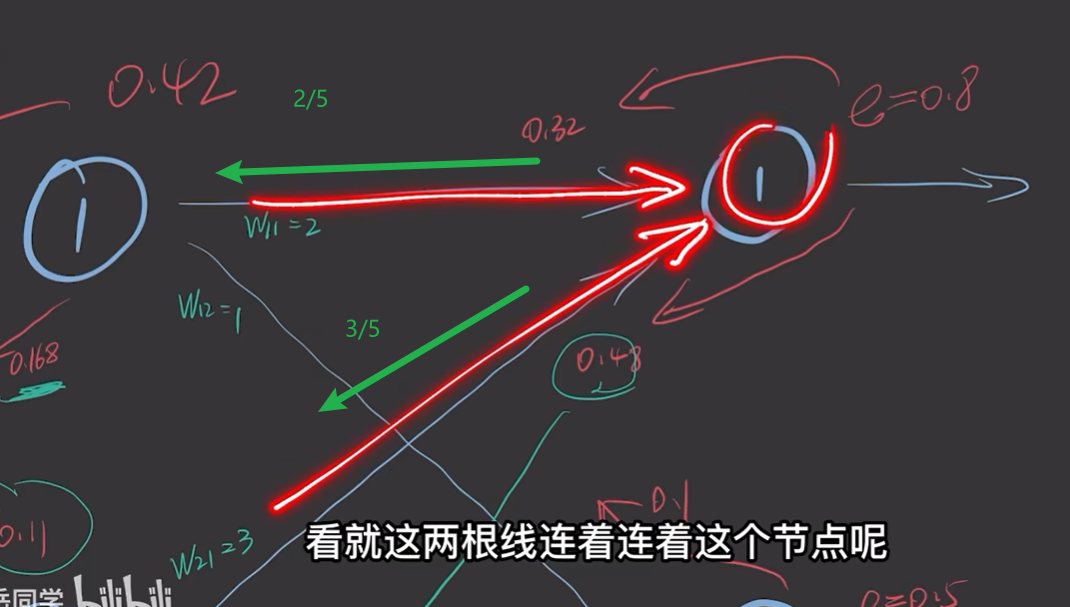
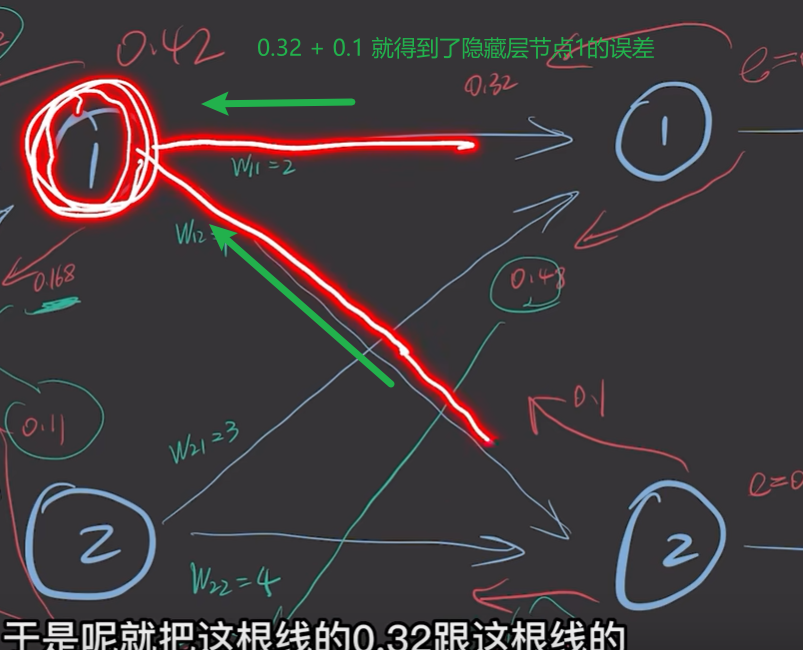
我们以同样的方式，就可以得到每个神经元的误差。如下图

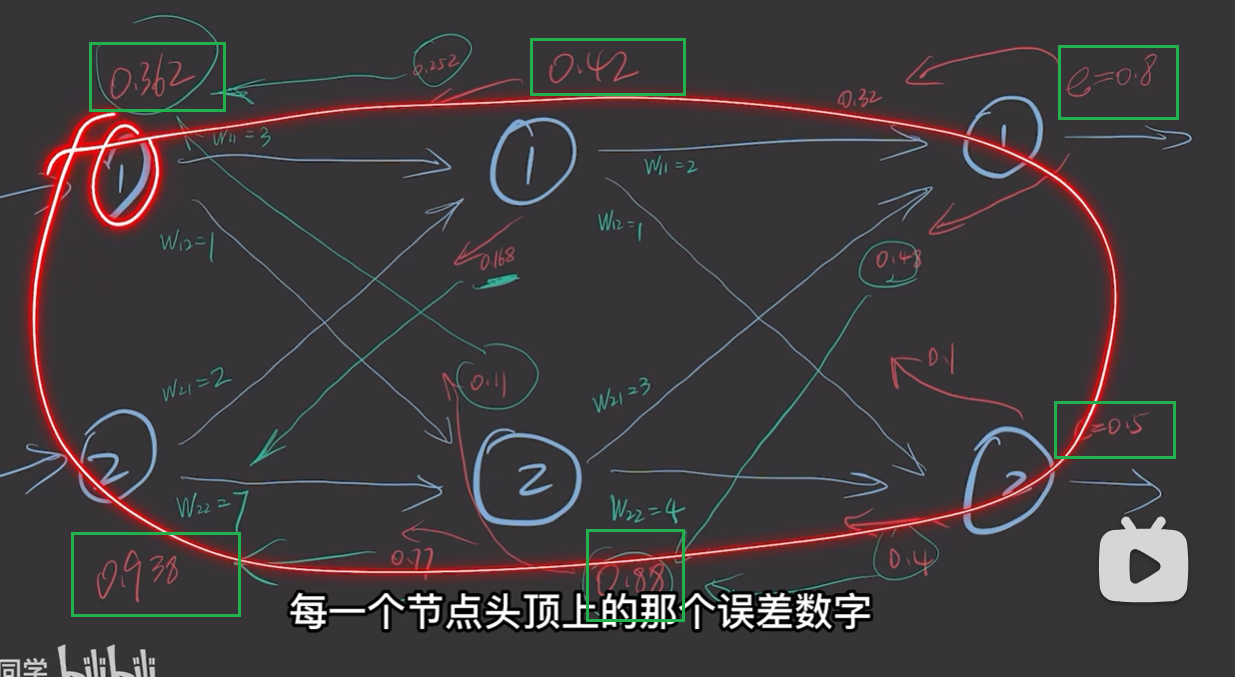
可以采用矩阵相乘的方法

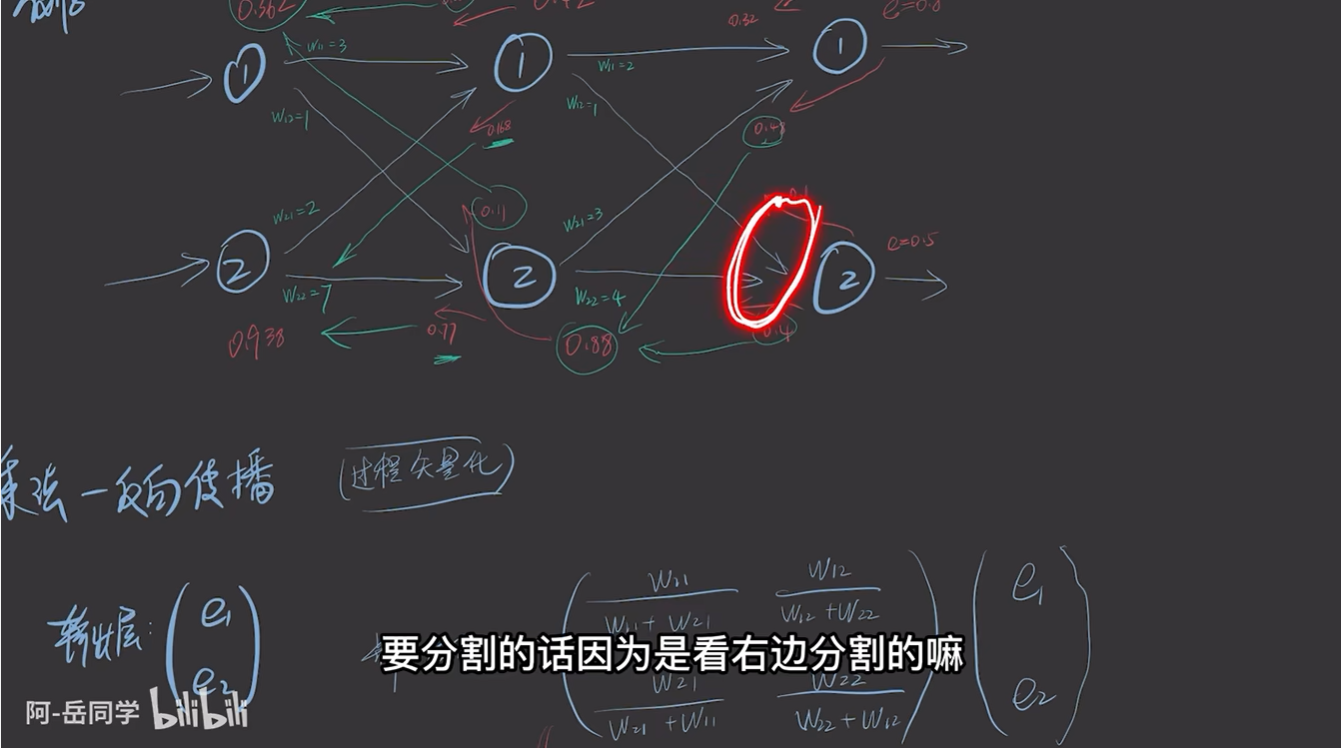
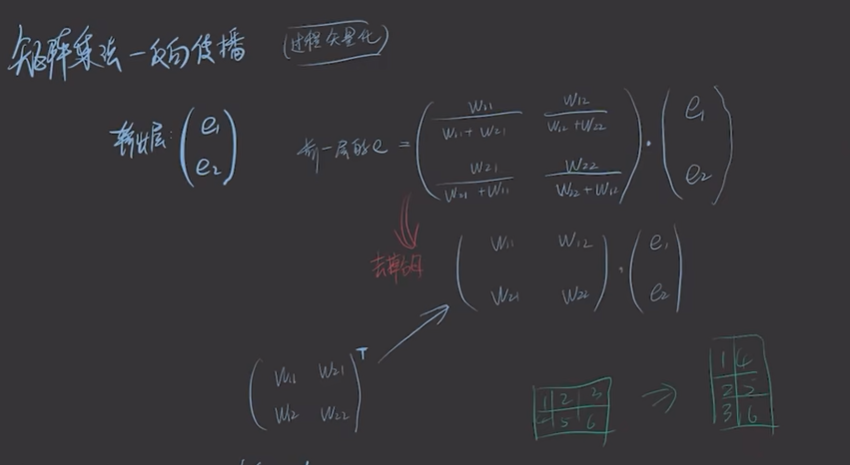
权重通过矩阵乘表示。

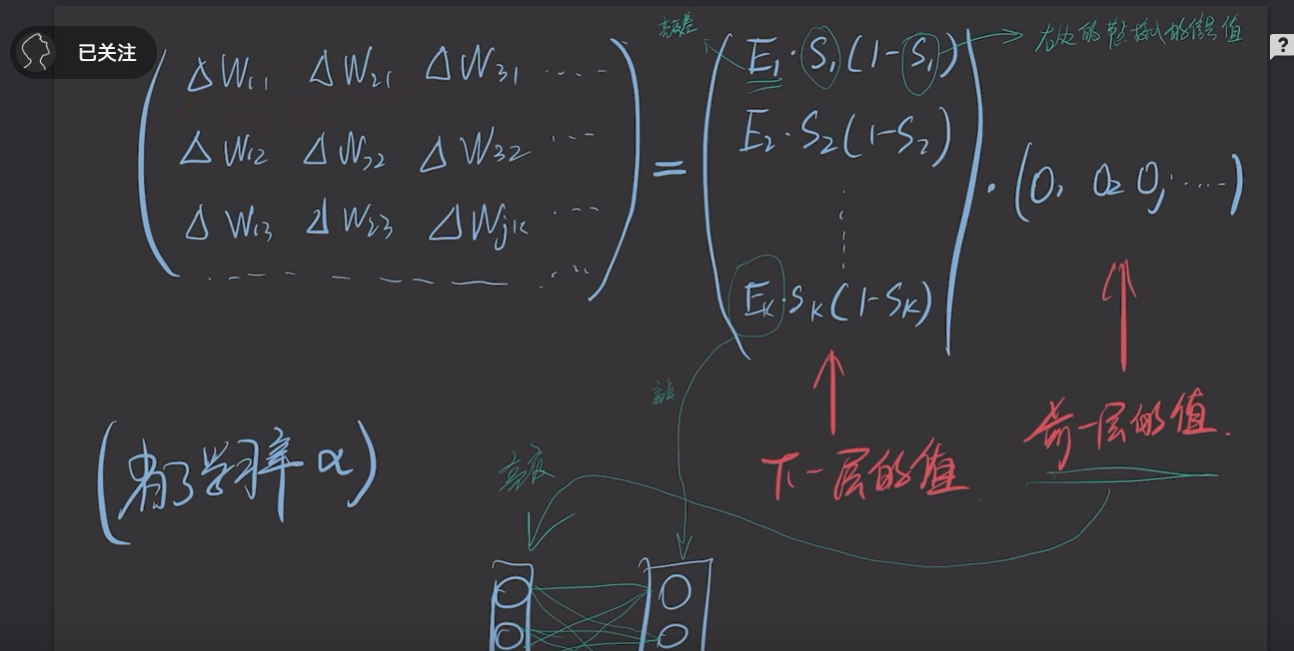
gpt辅助理解

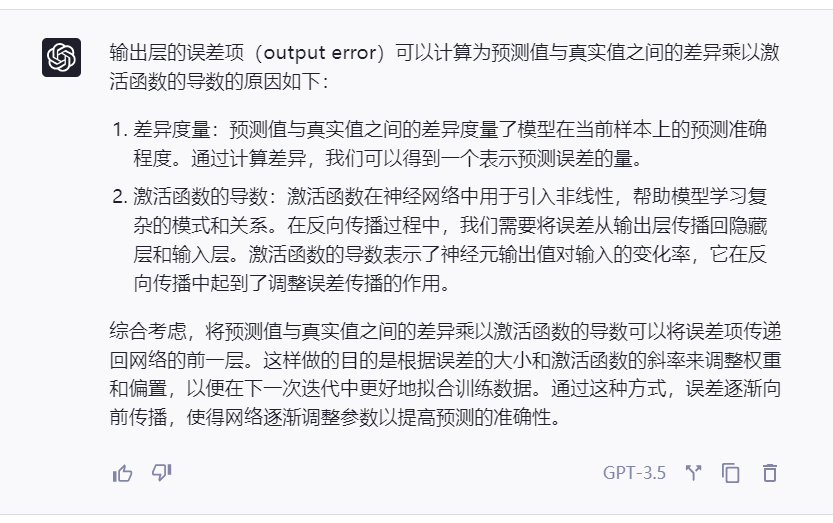
自己还是无法理解，但感觉输出层的误差项与选用的损失函数密切相关，因此，笔者询问了GPT，得到了如下的结果：

为什么要乘以激活函数的导数？

交叉熵损失函数的输出层误差项

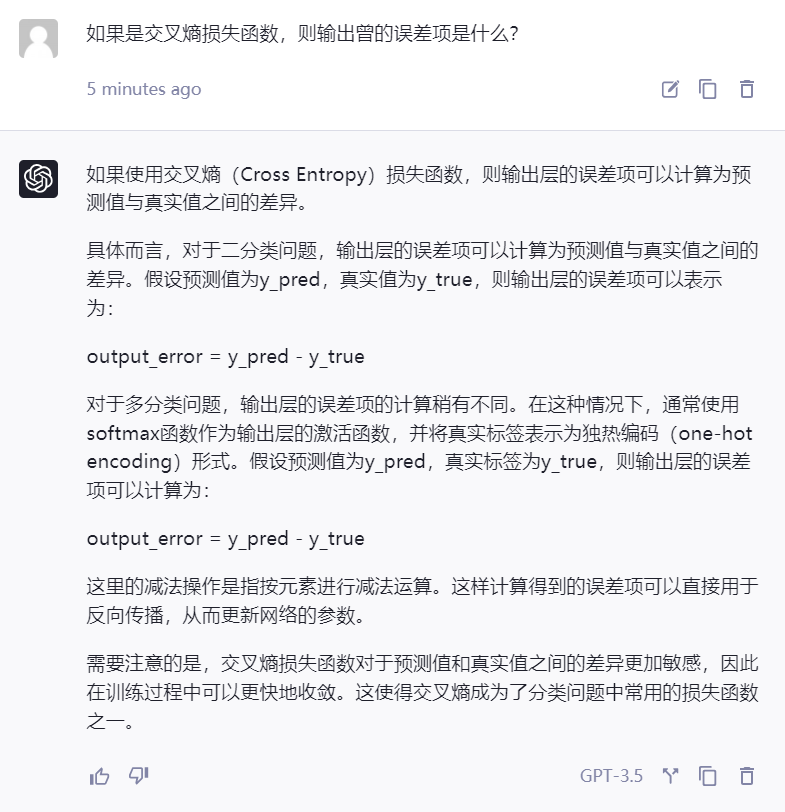
均方差输出层误差项：

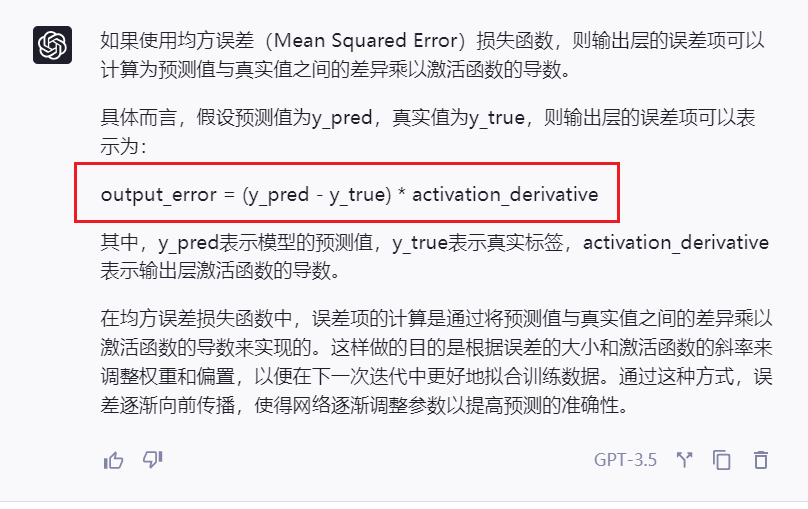
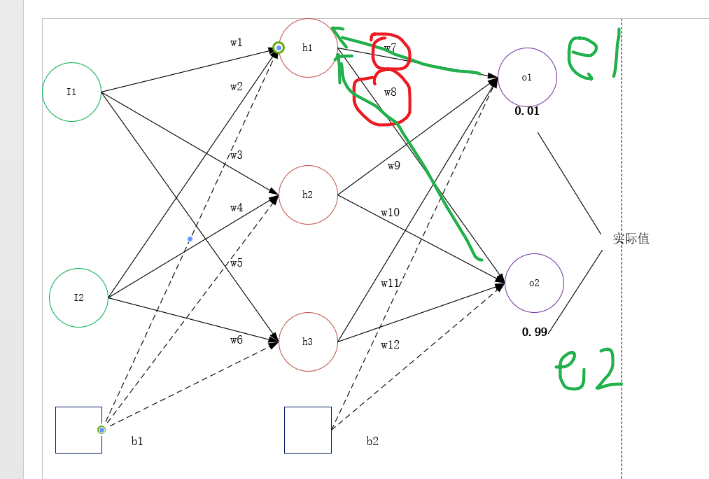
由此，我们可以得到如下的图示：

在计算h1节点的误差项时，输出层两个误差项以w7 和 w8进行作用，进而可以得到h1神经元的误差项：

error_h1=w₇*e₁ + w₈ * e₂。依次可以得到h1, h2, h3神经元的误差项损失。

动量因子

代码片段，其实整体贯彻了P166 图解机器学习图13.10，

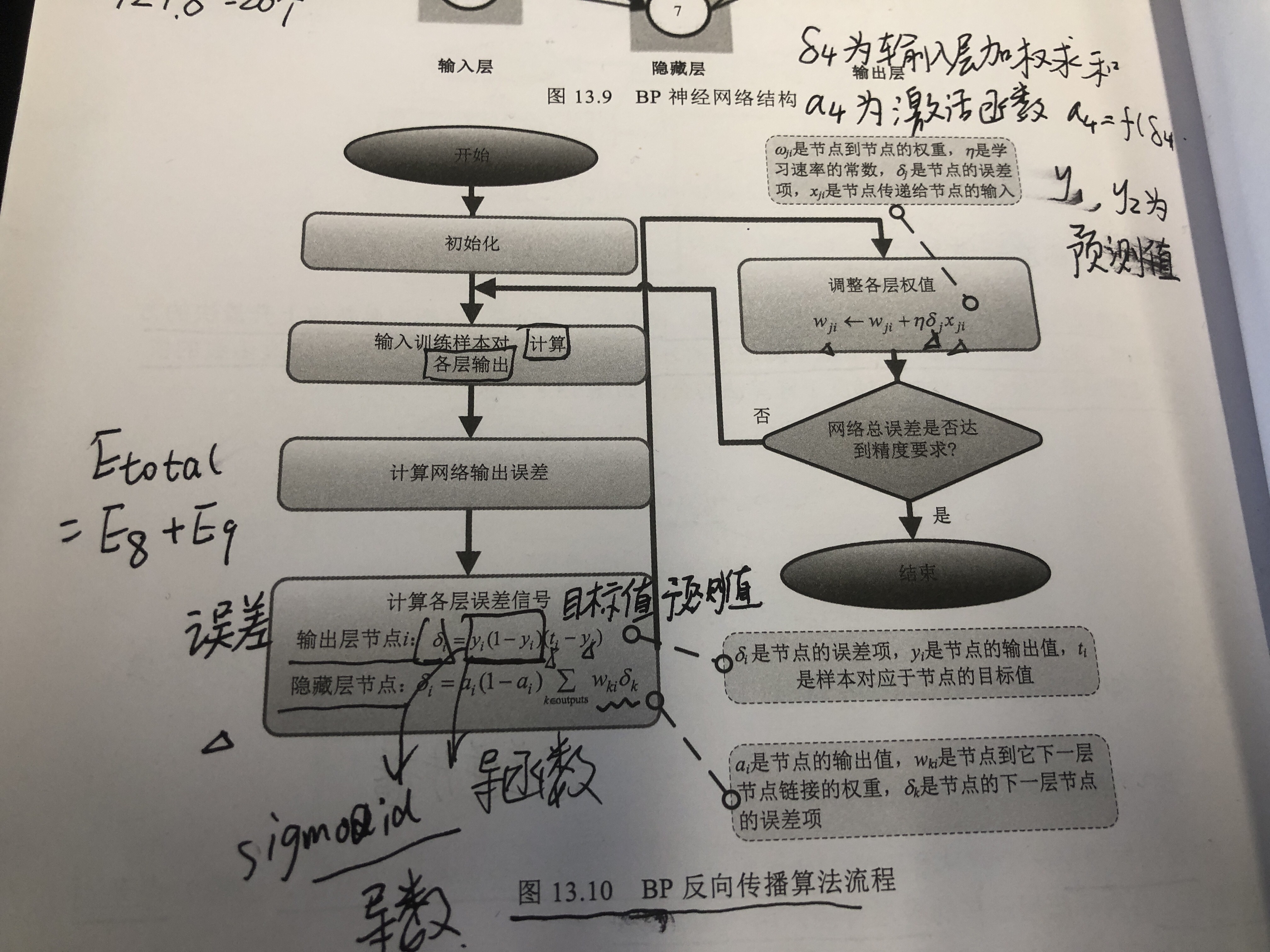
相互映照，也可以通过代码来理解上述的过程：

代码参见 11-06 周一神经网络之前向传播和反向传播代码实战

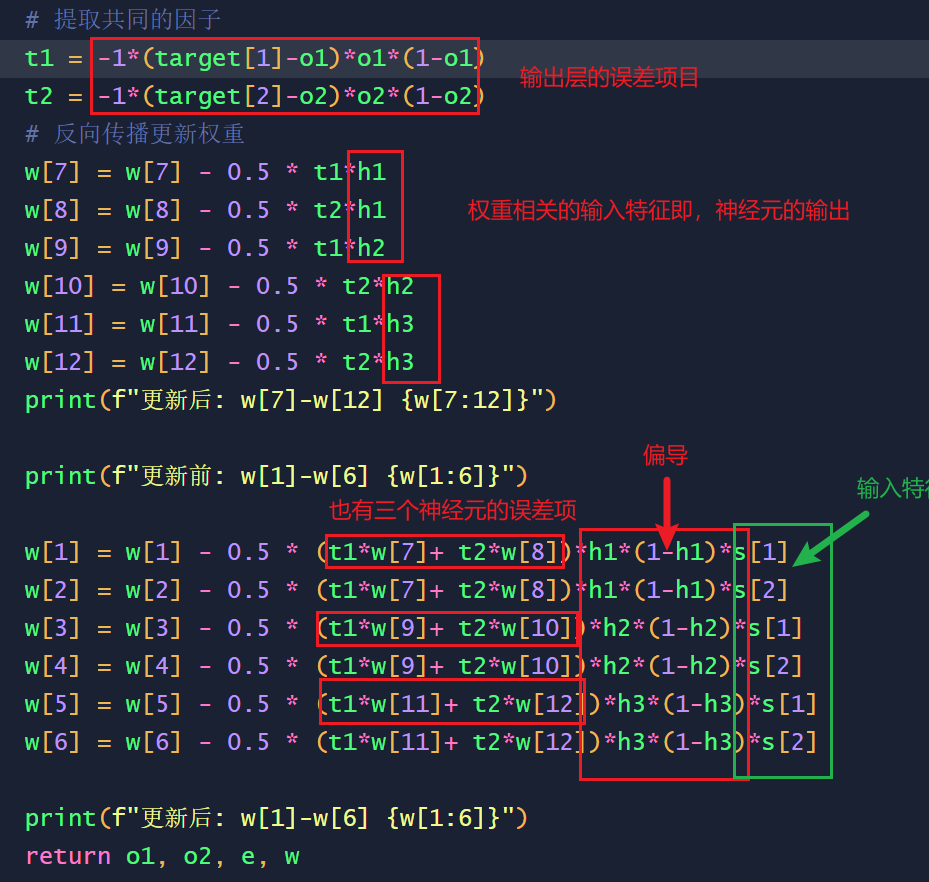
总结

这部分的代码片段比之前的全部手动计算权重更新的过程复杂一些，因为抽象出了输出层误差项和隐藏层误差项，代码的抽象知识更加复杂了，但 BP神经网络-第6集反向传播误差，调整全部权重则直接给出了误差项的矩阵乘表示，而这种方式，应该也是机器学习库中默认使用的方式吧。总之，这篇文章试图解释《图解机器学习》中第13章深度学习网络的代码，弄清楚其中权重更新的方式，包括为什么使用动量因子进行更新这种优化技术。希望读者能够读懂，进而在自己的工程实践中使用深度学习解决自己的问题。