这周自己被安排进行优化软件 IMU 姿态解算项目,之前自己只简单了解四元数,对IMU数据处理从未接触,通过这一周的学习感觉收获颇丰,在今天光棍节之际,,,用大半天的时间对这一周的收获进行整理,内容难免有错误还请大佬们指正, 抱拳感谢!!下面是自己学习过程主要参考的内容:参考链接1 、参考链接2 、参考链接3、参考链接4
一、元件简介
1.1 陀螺仪
陀螺仪,测量角速度,具有高动态特性,它是一个间接测量角度的器件。它测量的是角度的导数,即角速度,要将角速度对时间积分才能得到角度。
陀螺仪内部有一个陀螺,它的轴由于陀螺效应始终与初始方向平行,这样就可以通过与初始方向的偏差计算出旋转方向和角度。传感器MPU6050实际上是一个结构非常精密的芯片,内部包含超微小的陀螺。
如果这个世界是理想的美好的,从理论上讲只用陀螺仪是可以完成姿态导航的任务。只需要对3个轴的陀螺仪角速度进行积分,得到3个方向上的旋转角度,也就是姿态数据,即快速融合。不过现实是由于误差噪声等的存在,对陀螺仪积分并不能够得到完全准确的姿态,尤其是运转一段时间以后,积分误差的累加会让得到的姿态和实际的相差甚远。
那么哪些原因会使陀螺仪得到的姿态结果不准确呢?下面列举出常见的几种:
零点漂移
假设陀螺仪固定不动,理想角速度值是0dps(degree per second),但是存在零点漂移,例如有一个偏置0.1dps加在上面,于是测量出来是0.1dps,积分一秒之后,得到的角度是0.1度,1分钟之后是6度,还能忍受,一小时之后是360度,转了一圈,也就是说,陀螺仪在短时间内有很大的参考价值。
白噪声
电信号的测量中,一定会带有白噪声,陀螺仪数据的测量也不例外。所以获得的陀螺仪数据中也会带有白噪声,而且这种白噪声会随着积分而累加。
温度/加速度影响
陀螺仪是一个温度和加速度敏感的元器件。例如对于加速度,多轴机器人中的马达一般会带来较强烈的振动,一旦减震控制不好,就会在飞行过程中产生很大的加速度,必会带来陀螺输出的变化,引入误差。这就是在陀螺仪数据手册上常见的deg/sec/g指标。
积分误差
对陀螺仪角速度的积分是离散的,长时间的积分会出现漂移的情况。所以要考虑积分误差的问题。
这是由于陀螺仪测量姿态存在这么多的误差,所以必须要使用其它传感器辅助校正,其中最重要的就是加速度传感器。
1.2 加速度计
加速度计的低频特性好,可以测量低速的静态加速度。在机器人上即是对重力加速度g的测量和分析,其它瞬间加速度可以忽略。记住这一点对姿态解算融合理解非常重要。
在使用加速度计进行测量时,关注的是重力加速度在三个轴上的分量值。加速度计在自由落体时,其输出为0。为什么会这样呢?这里涉及到加速度计的设计原理:加速度计测量加速度是通过比力来测量,而不是通过加速度 (比力即载体受到的除重力以外的外力) , 惯导比力方程: f = a − g 惯导比力方程:\pmb{f=a-g} 惯导比力方程:f=a−g 。
加速度计仅仅测量的是重力加速度,3轴加速度计输出重力加速度在加速度计所在机体坐标系3个轴上的分量大小。重力加速度的方向和大小是固定的。通过这种关系,可以得到加速度计所在平面与地面的角度关系.
加速度计若是绕着重力加速度的轴转动,则测量值不会改变,也就是说加速度计无法感知这种水平旋转。
有关陀螺仪和加速度计和关系,姿态解算融合的原理,再把下面这个比喻放到这里一遍。
1.3 MPU6050
MPU-60x0是全球首例9轴运动处理传感器。它集成了3轴MEMS陀螺仪,3轴MEMS加速度计,以及一个可扩展的数字运动处理器DMP(Digital Motion Processor),可用I2C接口连接一个第三方的数字传感器,比如磁力计。扩展之后就可以通过其I2C或SPI接口输出一个9轴的信号(SPI接口仅在MPU-6000可用)。MPU-60x0也可以通过其I2C接口连接非惯性的数字传感器,比如压力传感器。
MPU-60x0对陀螺仪和加速度计分别用了三个16位的ADC,将其测量的模拟量转化为可输出的数字量。为了精确跟踪快速和慢速的运动,传感器的测量范围都是用户可控的,陀螺仪可测范围为±250,±500,±1000,±2000°/秒(dps),加速度计可测范围为±2,±4,±8,±16g。一个片上1024字节的FIFO,有助于降低系统功耗。和所有设备寄存器之间的通信采用400kHz的I2C接口或1MHz 的SPI接口(SPI仅MPU-6000可用)。对于需要高速传输的应用,对寄存器的读取和中断可用20MHz的SPI。另外,片上还内嵌了一个温度传感器和在工作环境下仅有±1%变动的振荡器。
MPU6050/HMC5883/MS5611传感器之间的连接如下图所示。

1.4 DMP硬件解算
软件解算四元数,即从IIC总线上读到的MPU60x0的AD值,然后通过四元数解算姿态角这种实现方式。

MPU6050的硬解四元数,即从IIC总线上读到的数据不再是MPU60x0的AD值,而是通过初始化对DMP引擎的配置,从IIC总线上读到的直接就是四元数的值,从而跳过了程序通过AD值计算四元数这个看起来繁琐的步骤。机身反应的确要比之前反应灵活,最关键的一点是,这样得出的偏航角(Yaw)很稳很稳,基本不会漂移或者说漂移小到了可以容忍的地步。
最后,MPU60x0的强大之处不仅于此,它支持一个从IIC接口,可以外部接上一个磁力计,如HMC5883,这样一来,DMP引擎可以直接输出一个绝对的方向姿态,即能够输出一个带东西南北的姿态数据包。

接下来,需要讲清楚什么是姿态,怎么表示姿态,如何得到姿态。
二、姿态及其表示
2.1 什么是姿态
姿态就是指机器人运行过程中的俯仰/横滚/航向情况。机器人需要实时知道当前自己的姿态,才能够根据需要操控其接下来的动作,例如保持平稳,例如实现翻滚。
数学模型
姿态是用来描述一个刚体的固连坐标系和参考坐标系之间的角位置关系,有一些数学表示方法。常见的如欧拉角,四元数,矩阵,轴角。
地球坐标系又叫做地理坐标系、世界坐标系是固定不变的。正北,正东,正向上构成了这个坐标系的X,Y,Z轴,用坐标系n表示。机器人上固定着一个坐标系,一般称之为机体坐标系,用坐标系b表示。那么就可用欧拉角,四元数等来描述b和n的角位置关系。这就是姿态解算的数学模型和基础。

2.2 姿态表示方式
姿态有多种数学表示方式,常见的是四元数,欧拉角,矩阵和轴角。他们各自有其自身的优点,在不同的领域使用不同的表示方式。在机器人中使用到了四元数和欧拉角。
四元数
四元数是由爱尔兰数学家威廉·卢云·哈密顿在1843年发现的数学概念。从明确地角度而言,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
四元数大量用于电脑绘图(及相关的图像分析)上表示三维物件的旋转及方位。四元数亦见于控制论、信号处理、姿态控制、物理和轨道力学,都是用来表示旋转和方位。相对于另几种旋转表示法(矩阵,欧拉角,轴角),四元数具有某些方面的优势,如速度更快、提供平滑插值、有效避免万向锁问题、存储空间较小等等。
欧拉角
莱昂哈德·欧拉用欧拉角来描述刚体在三维欧几里得空间的取向。对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系又称为实验室参考系,是静止不动的。而坐标系则固定于刚体,随着刚体的旋转而旋转。

下面通过图例来看看欧拉角是如何产生的,并且分别对应哪个角度。

2.3 姿态解算
姿态解算需要解决的是机器人在地球坐标系中姿态。姿态解算的英文是attitude algorithm,也叫做姿态分析,姿态估计,姿态融合。姿态解算是指根据IMU数据(陀螺仪、加速度计、罗盘等)求解出机器人的姿态,所以也叫做IMU数据融合(IMU Data Fusing)。
角位置关系测量
如上所说,地球坐标系n是固定的。机器人上固定一个坐标系b,这个坐标系b在坐标系n中运动。那么如何知道坐标系b和坐标系n的角位置关系呢,也就是怎么知道机器人相对于地球这个固定坐标系R转动了一下航向,或者侧翻了一下机身。这就是传感器需要测量的数据,传感器包括陀螺仪,加速度计,磁力计。通过获得这些测量数据,得到坐标系b和坐标系n的角位置关系。
惯性测量模块:IMU(Inertial Measurement Unit),提供机器人姿态的传感器原始数据,一般由陀螺仪传感器/加速度传感器/磁力计提供机器人9DOF数据。
机器人根据陀螺仪的三轴角速度对时间积分得到的俯仰/横滚/航向角,这是快速解算。快速解算得到的姿态是存在误差的,而且误差会累加。如果再结合三轴地磁和三轴加速度数据进行校正,得到准确的姿态,这就是深度解算。
当然,快速解算的姿态一般是不能够用于控制机器人的,因为误差太大。所以,一般说的姿态解算是深度解算。
四元数和欧拉角在姿态解算中如何使用
姿态解算的核心在于旋转,一般旋转有4种表示方式:矩阵表示、欧拉角表示、轴角表示和四元数表示。矩阵表示适合变换向量,欧拉角最直观,轴角表示则适合几何推导,而在组合旋转方面,四元数表示最佳。因为姿态解算需要频繁组合旋转和用旋转变换向量,所以采用四元数保存机器人的姿态。
一般来说,使用四元数来保存机器人的姿态(即在地球坐标系中的俯仰/横滚/航向情况)。在需要控制的时候,会将四元数转化为欧拉角,然后输入到姿态控制算法中。
姿态控制算法的输入参数必须要是欧拉角。
下面就是常见机器人姿态解算到姿态控制的整个流程。AD值是指MPU6050的陀螺仪和加速度值,3个维度的陀螺仪值和3个维度的加速度值,每个值为16位精度。AD值通过姿态解算算法得到机器人当前的姿态(姿态使用四元数表示),然后将四元数转化为欧拉角,用于姿态控制算法(PID控制)中。

2.4 余弦矩阵
下面介绍由三轴陀螺仪和加速度计的值来使用软件算法解算姿态的方法。
先逐步认识如何用欧拉角描述一次平面旋转(坐标变换):

设坐标系绕旋转 ψ \psi ψ角后得到坐标系,在空间中有一个矢量在坐标系中的投影为,在内的投影为由于旋转绕进行,所以Z坐标未变,即有。
x ′ = O C + C D + D E = O A c o s ψ + A D s i n ψ + D G s i n ψ = O A c o s ψ + ( A D + D G ) s i n ψ = x c o s ψ + y s i n ψ x^{'}=OC+CD+DE =OAcos\psi+ADsin\psi+DGsin\psi \\=OAcos\psi+(AD+DG)sin\psi =xcos\psi+ysin\psi x′=OC+CD+DE=OAcosψ+ADsinψ+DGsinψ=OAcosψ+(AD+DG)sinψ=xcosψ+ysinψ
y ′ = A F − A C = A G c o s ψ − O A c o s ψ = y c o s ψ − x s i n ψ y^{'}=AF-AC=AGcos\psi-OAcos\psi \\ =ycos\psi-xsin\psi y′=AF−AC=AGcosψ−OAcosψ=ycosψ−xsinψ
转换成矩阵形式表示为:
[ x ′ y ′ z ′ ] = [ c o s ψ s i n ψ 0 − s i n ψ c o s ψ 0 0 0 1 ] [ x y z ] \left[\begin{matrix} x^{'} \\ y^{'} \\ z^{'} \end{matrix} \right] =\left[ \begin{matrix} cos\psi && sin\psi && 0 \\ -sin\psi && cos\psi && 0\\ 0 && 0 && 1 \end{matrix} \right] \left[\begin{matrix} x \\ y \\ z \end{matrix} \right] x′y′z′ = cosψ−sinψ0sinψcosψ0001 xyz
上面仅仅是绕一根轴的旋转,如果三维空间中的欧拉角旋转要转三次:
R ( ψ ) = [ c o s ψ s i n ψ 0 − s i n ψ c o s ψ 0 0 0 1 ] R ( θ ) = [ c o s θ 0 − s i n θ 0 1 0 s i n θ 0 c o s θ ] R ( γ ) = [ 1 0 0 0 c o s γ s i n γ 0 − s i n γ c o s γ ] \begin{aligned} R(\psi)&=\begin{bmatrix}cos\psi&sin\psi&0\\-sin\psi&cos\psi&0\\0&0&1\end{bmatrix} \\ R(\theta)&=\begin{bmatrix}cos\theta&0&-sin\theta\\ 0&1&0\\sin\theta&0&cos\theta\end{bmatrix}\\ R(\gamma)&=\begin{bmatrix}1&0&0\\ 0&cos\gamma&sin\gamma\\0&-sin\gamma&cos\gamma\end{bmatrix}\\ \end{aligned} R(ψ)R(θ)R(γ)= cosψ−sinψ0sinψcosψ0001 = cosθ0sinθ010−sinθ0cosθ = 1000cosγ−sinγ0sinγcosγ
由于矩阵乘法不满足交换律,所以旋转顺序不同,得到的姿态也不同,一般按照"ZYX"的顺序进行旋转。假设将世界坐标系下的向量 v n v^n vn 按照欧拉角 ϕ , θ , ψ \phi, \theta, \psi ϕ,θ,ψ旋转到机体坐标系得到 v b v^b vb 。
首先绕世界坐标系的Z轴旋转 ψ \psi ψ,得到 v b ′ v^{b'} vb′:
v b ′ = R ( ψ ) v n v^{b'}=R(\psi)v^n vb′=R(ψ)vn
继续绕世界坐标系的Y轴旋转 θ \theta θ,得到 v b ′ ′ v^{b''} vb′′ :
v b ′ ′ = R ( θ ) v b ′ = R ( θ ) R ( ψ ) v n v^{b''}=R(\theta)v^{b'}=R(\theta)R(\psi)v^n vb′′=R(θ)vb′=R(θ)R(ψ)vn
最后绕世界坐标系的X轴旋转 ϕ \phi ϕ,得到 v b v^b vb :
v b = R ( ϕ ) v b ′ ′ = R ( ϕ ) R ( θ ) R ( ψ ) v n v^b=R(\phi)v^{b''}=R(\phi)R(\theta)R(\psi)v^n vb=R(ϕ)vb′′=R(ϕ)R(θ)R(ψ)vn
所以从世界坐标系到机体坐标系的旋转矩阵为:
R = R ( ϕ ) R ( θ ) R ( ψ ) = [ c o s θ c o s φ − c o s ϕ s i n ψ + s i n ϕ s i n θ c o s ψ s i n ϕ s i n ψ + c o s ϕ s i n θ c o s ψ c o s θ s i n ψ c o s ϕ c o s ψ + s i n ϕ s i n θ s i n ψ − s i n ϕ c o s ψ + c o s ϕ s i n θ s i n ψ − s i n θ s i n ϕ c o s θ c o s ϕ c o s θ ] \begin{aligned} R&=R(\phi)R(\theta)R(\psi)\\ &=\begin{bmatrix} cos\theta cos\varphi&-cos\phi sin\psi+sin\phi sin\theta cos\psi&sin\phi sin\psi +cos\phi sin\theta cos\psi\\ cos\theta sin\psi&cos\phi cos\psi+sin\phi sin\theta sin\psi&-sin\phi cos\psi+cos\phi sin\theta sin\psi\\ -sin\theta&sin\phi cos\theta &cos\phi cos\theta \end{bmatrix} \end{aligned} R=R(ϕ)R(θ)R(ψ)= cosθcosφcosθsinψ−sinθ−cosϕsinψ+sinϕsinθcosψcosϕcosψ+sinϕsinθsinψsinϕcosθsinϕsinψ+cosϕsinθcosψ−sinϕcosψ+cosϕsinθsinψcosϕcosθ
上面得到了一个表示旋转的方向余弦矩阵。
不过要想用欧拉角解算姿态,其实我们套用欧拉角微分方程就行了:

上式中左侧,是本次更新后的欧拉角,对应row,pit,yaw。右侧,是上个周期测算出来的角度,三个角速度由直接安装在机器人的三轴陀螺仪在这个周期转动的角度,单位为弧度,计算间隔时T_陀螺角速度,比如0.02秒_ 0.01弧度/秒=0.0002弧度。因此求解这个微分方程就能解算出当前的欧拉角。
前面介绍了什么是欧拉角,而且欧拉角微分方程解算姿态关系简单明了,概念直观容易理解,那么我们为什么不用欧拉角来表示旋转而要引入四元数呢?一方面是因为欧拉角微分方程中包含了大量的三角运算,这给实时解算带来了一定的困难。而且当俯仰角为90度时方程式会出现“GimbalLock”。所以欧拉角方法只适用于水平姿态变化不大的情况,而不适用于全姿态机器人的姿态确定,故一般采用四元数进行实时解算。
将欧拉角描述的方向余弦矩阵用四元数描述则为:
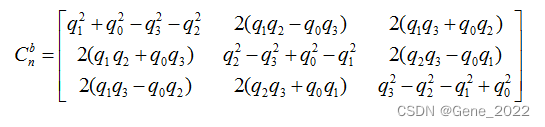
三、四元数微分方程
3.1 四元数三角化表达
某四元数为 Q = q 0 + q = q 0 + q 1 i + q 2 j + q 3 k \pmb{Q}=q_0+\pmb{q}=q_0+q_1\pmb{i}+q_2\pmb{j}+q_3\pmb{k} Q=q0+q=q0+q1i+q2j+q3k (式中, i , j , k \pmb{i,j,k} i,j,k是正交单位矢量)。
四元数的范数: ∣ ∣ Q ∣ ∣ = q 0 2 + q 1 2 + q 2 2 + q 3 2 ||Q||=q_0^2+q_1^2+q_2^2+q_3^2 ∣∣Q∣∣=q02+q12+q22+q32
四元数的模: ∣ Q ∣ = q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1 |Q|=\sqrt{q_0^2+q_1^2+q_2^2+q_3^2}=1 ∣Q∣=q02+q12+q22+q32=1
按 Q \pmb{Q} Q 定向的单位向量 n = q 1 i + q 2 j + q 3 k q 1 2 + q 2 2 + q 3 2 \pmb{n}=\frac{q_1\pmb{i}+q_2\pmb{j}+q_3\pmb{k}}{\sqrt{q_1^2+q_2^2+q_3^2}} n=q12+q22+q32q1i+q2j+q3k
令, c o s θ 2 = q 0 ∣ Q ∣ cos\frac{\theta}{2}=\frac{q_0}{|Q|} cos2θ=∣Q∣q0 , s i n θ 2 = q 1 2 + q 2 2 + q 3 2 ∣ Q ∣ sin\frac{\theta}{2}=\frac{\sqrt{q_1^2+q_2^2+q_3^2}}{|Q|} sin2θ=∣Q∣q12+q22+q32 ,则
Q = ∣ Q ∣ ( q 0 ∣ Q ∣ + q 1 i + q 2 j + q 3 k q 1 2 + q 2 2 + q 3 2 q 1 2 + q 2 2 + q 3 2 ∣ Q ∣ ) = ∣ Q ∣ ( c o s θ 2 + n s i n θ 2 ) = c o s θ 2 + n s i n θ 2 = cos θ 2 + n ^ sin θ 2 \pmb{Q}=|Q|\left(\frac{q_0}{|Q|}+\frac{q_1\pmb{i}+q_2\pmb{j}+q_3\pmb{k}}{\sqrt{q_1^2+q_2^2+q_3^2}}\frac{\sqrt{q_1^2+q_2^2+q_3^2}}{|Q|}\right)=|Q|(cos\frac{\theta}{2}+\pmb{n}sin\frac{\theta}{2})=cos\frac{\theta}{2}+\pmb{n}sin\frac{\theta}{2}=\cos \frac{\theta}{2}+\hat{n} \sin \frac{\theta}{2} Q=∣Q∣(∣Q∣q0+q12+q22+q32q1i+q2j+q3k∣Q∣q12+q22+q32)=∣Q∣(cos2θ+nsin2θ)=cos2θ+nsin2θ=cos2θ+n^sin2θ
欧拉公式:
e i θ = c o s θ + i s i n θ e^{\pmb{i}\theta}=cos\theta+\pmb{i}sin\theta eiθ=cosθ+isinθ
故,四元数指数式:
Q = e n ^ θ 2 \pmb{Q}=e^{\hat{n}\frac{\theta}{2}} Q=en^2θ
PS:为什么四元数的三角式是 Q = cos θ 2 + n ^ sin θ 2 \mathbf{Q} = \cos \frac{\theta}{2} + \hat{n} \sin \frac{\theta}{2} Q=cos2θ+n^sin2θ , 不是 Q = c o s θ + n ^ s i n θ \mathbf{Q} = cos\theta+ \hat{n} sin\theta Q=cosθ+n^sinθ ?
答:关于四元数的三角形式是 Q = cos θ 2 + n ^ sin θ 2 \mathbf{Q} = \cos \frac{\theta}{2} + \hat{n} \sin \frac{\theta}{2} Q=cos2θ+n^sin2θ ,而不是 Q = c o s θ + n ^ s i n θ \pmb{Q} =cos \theta + \hat{n} sin \theta Q=cosθ+n^sinθ ,是因为四元数可以用来表示三维空间中的旋转。前者描述了四元数旋转的性质,而后者则没有适当地捕捉到这种旋转特性,(在这里, θ \theta θ 是旋转的角度,而 n ^ \hat{n} n^ 是一个单位向量,表示旋转轴的方向)。
考虑一个四元数的旋转操作,如果我们将 θ \theta θ 乘以2,即 θ → 2 θ \theta \rightarrow 2\theta θ→2θ ,那么 c o s θ 2 cos \frac{\theta}{2} cos2θ 会变成 cos θ \cos \theta cosθ ,而 s i n θ 2 sin \frac{\theta}{2} sin2θ 会变成 s i n θ sin \theta sinθ。这样,你会得到 Q = c o s θ + n ^ s i n θ \pmb{Q} = cos \theta + \hat{n} sin \theta Q=cosθ+n^sinθ。但这实际上表示的是一个两倍角度的旋转,而不是原来的旋转。
为了保持旋转的性质,我们使用 c o s θ 2 cos \frac{\theta}{2} cos2θ 和 s i n θ 2 sin \frac{\theta}{2} sin2θ。这种形式的好处是,当我们对一个四元数连续进行旋转时,它们会累积旋转效果而不是叠加角度。这种表达方式更加适合描述旋转运算。
(此部分是我问ChatGPT的回答结果,,,自己保持存疑态度,对此明白的大佬解惑一下谢谢!)
3.2 四元数微分
已知,从 n n n 系到 b b b 系的旋转四元数可以表示为:
Q = cos θ 2 + n ^ sin θ 2 \pmb{Q}=\cos \frac{\theta}{2}+\hat{n} \sin \frac{\theta}{2} \\ Q=cos2θ+n^sin2θ
上式 n ^ \hat{n} n^ 中为旋转轴, θ θ θ为旋转角,对两边求导可得:
d Q d t = − θ ˙ 2 sin θ 2 + n ^ θ ˙ 2 cos θ 2 + sin θ 2 d n ^ d t \frac{d \pmb{Q}}{d t}=-\frac{\dot{\theta}}{2} \sin \frac{\theta}{2}+\hat{n} \frac{\dot{\theta}}{2} \cos \frac{\theta}{2}+\sin \frac{\theta}{2} \frac{d \hat{n}}{d t} \\ dtdQ=−2θ˙sin2θ+n^2θ˙cos2θ+sin2θdtdn^
根据哥氏定理可得:
d n ^ d t = C b n d n b d t + ω n b n × n ^ \frac{d \hat{n}}{d t}=C_{b}^{n} \frac{d n^{b}}{d t}+\omega_{n b}^{n} \times \hat{n} \\ dtdn^=Cbndtdnb+ωnbn×n^
由于刚体绕轴旋转,与刚体固联的 b b b 坐标系的各个轴在旋转的过程中分别位于三个不同的圆锥面上,三个圆锥面的定点即为 b b b 系的原点,为其共同的对称轴,这块大家可以想象一下,还是挺容易想象的,这样到 b b b 坐标系三个轴上的投影不变,长度为各自圆锥底面半径,所以有:
d n b d t = 0 \frac{d n^{b}}{d t}=0 dtdnb=0
又有:
ω n b n = θ ˙ n ^ \omega_{n b}^{n}=\dot{\theta} \hat{n} \\ ωnbn=θ˙n^
上式中的意思是: n n n 系到 b b b 系的角速度在 n n n 系上的投影。所以:
d n ^ d t = θ ˙ n ^ × n ^ = 0 \frac{d \hat{n}}{d t}=\dot{\theta} \hat{n} \times \hat{n}=0 \\ dtdn^=θ˙n^×n^=0
或者,也可以直接理解为:因为旋转轴 n ^ \hat{n} n^ 始终未变,所以 d n ^ d t = 0 \frac{d \hat{n}}{d t}=0 dtdn^=0 。
因此
d Q d t = − θ ˙ 2 sin θ 2 + n ^ θ ˙ 2 cos θ 2 \frac{d \pmb{Q}}{d t}=-\frac{\dot{\theta}}{2} \sin \frac{\theta}{2}+\hat{n} \frac{\dot{\theta}}{2} \cos \frac{\theta}{2} dtdQ=−2θ˙sin2θ+n^2θ˙cos2θ
设 , n ^ ⊗ n ^ \hat{n} \otimes \hat{n} n^⊗n^ 表示纯单位四元数相乘,根据四元数乘法法则容易推出 n ^ ⊗ n ^ = − 1 \hat{n} \otimes \hat{n}=-1 n^⊗n^=−1,详细证明可见附录,所以
d Q d t = − θ ˙ 2 sin θ 2 + n ^ θ ˙ 2 cos θ 2 = θ ˙ 2 cos θ 2 n ^ + n ^ ⊗ n ^ θ ˙ 2 sin θ 2 = θ ˙ 2 n ^ ⊗ ( cos θ 2 + n ^ sin θ 2 ) = θ ˙ 2 n ^ ⊗ Q = 1 2 ω n b n ⊗ Q \frac{d \pmb{Q}}{d t}=-\frac{\dot{\theta}}{2} \sin \frac{\theta}{2}+\hat{n} \frac{\dot{\theta}}{2} \cos \frac{\theta}{2}=\frac{\dot{\theta}}{2} \cos \frac{\theta}{2} \hat{n}+\hat{n} \otimes \hat{n} \frac{\dot{\theta}}{2} \sin \frac{\theta}{2} \\ = \frac{\dot{\theta}}{2} \hat{n} \otimes\left(\cos \frac{\theta}{2}+\hat{n} \sin \frac{\theta}{2}\right)=\frac{\dot{\theta}}{2} \hat{n} \otimes Q=\frac{1}{2} \omega_{n b}^{n} \otimes \pmb{Q} dtdQ=−2θ˙sin2θ+n^2θ˙cos2θ=2θ˙cos2θn^+n^⊗n^2θ˙sin2θ=2θ˙n^⊗(cos2θ+n^sin2θ)=2θ˙n^⊗Q=21ωnbn⊗Q
上面公式中的 ω n b n \omega_{n b}^{n} ωnbn 是在世界坐标系下的角速度,而IMU中的陀螺仪测量得到的角速度是在机体坐标系的,所以还需要一个转换关系,根据坐标变换的四元数乘法表示法:
r n = Q ⊗ r b ⊗ Q ∗ r^{n}=\pmb{Q} \otimes r^{b} \otimes \pmb{Q}^{*} \\ rn=Q⊗rb⊗Q∗
上式中 Q ∗ Q^{*} Q∗为 Q Q Q 的共轭四元数,需要注意上公式中的 Q Q Q 依然是从 n n n 系到 b b b 系转换的四元数, r b r^{b} rb 和 r n r^{n} rn是实部为0的四元数。
所以
ω n b n = Q ⊗ ω n b b ⊗ Q ∗ \omega_{n b}^{n}=\pmb{Q} \otimes \omega_{n b}^{b} \otimes \pmb{Q}^{*} \\ ωnbn=Q⊗ωnbb⊗Q∗
带入 d Q d t \frac{d \pmb{Q}}{d t} dtdQ的公式得:
d Q d t = 1 2 ω n b n ⊗ Q = 1 2 Q ⊗ ω n b b ⊗ Q ∗ ⊗ Q \frac{d \pmb{Q}}{d t}=\frac{1}{2} \omega_{n b}^{n} \otimes \pmb{Q}=\frac{1}{2} \pmb{Q} \otimes \omega_{n b}^{b} \otimes \pmb{Q}^{*} \otimes \pmb{Q} \\ dtdQ=21ωnbn⊗Q=21Q⊗ωnbb⊗Q∗⊗Q
由于 Q \pmb{Q} Q 为单位四元数, Q ∗ \pmb{Q}^{*} Q∗ 为单位四元数的逆,所以 Q ∗ ⊗ Q = 1 \pmb{Q}^{*} \otimes \pmb{Q}=1 Q∗⊗Q=1 。
d Q d t = 1 2 Q ⊗ ω n b b \frac{d \pmb{Q}}{d t}=\frac{1}{2} \pmb{Q} \otimes \omega_{n b}^{b} dtdQ=21Q⊗ωnbb
ω n b b \omega_{n b}^{b} ωnbb为陀螺仪的测量值,记
[ 0 ω x ω y ω z ] \left[\begin{array}{c} {0} \\ {\omega_{x}} \\ {\omega_{y}} \\ {\omega_{z}} \end{array}\right] \\ 0ωxωyωz
根据四元数的乘法定义, d Q d t \frac{d \pmb{Q}}{d t} dtdQ有两种表示形式,第一种 如下所示:
d Q d t = 1 2 M ′ ( ω n b b ) Q \frac{d \pmb{Q}}{d t}=\frac{1}{2} M^{\prime}\left(\omega_{n b}^{b}\right) \pmb{Q} \\ dtdQ=21M′(ωnbb)Q
即
[ q ˙ 0 q ˙ 1 q ˙ 2 q ˙ 3 ] = 1 2 [ 0 − ω x − ω y − ω z ω x 0 ω z − ω y ω y − ω z 0 ω x ω z ω y − ω x 0 ] [ q 0 q 1 q 2 q 3 ] \left[\begin{array}{c} {\dot{q}_{0}} \\ {\dot{q}_{1}} \\ {\dot{q}_{2}} \\ {\dot{q}_{3}} \end{array}\right]=\frac{1}{2}\left[\begin{array}{cccc} {0} & {-\omega_{x}} & {-\omega_{y}} & {-\omega_{z}} \\ {\omega_{x}} & {0} & {\omega_{z}} & {-\omega_{y}} \\ {\omega_{y}} & {-\omega_{z}} & {0} & {\omega_{x}} \\ {\omega_{z}} & {\omega_{y}} & {-\omega_{x}} & {0} \end{array}\right]\left[\begin{array}{l} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right] \\ q˙0q˙1q˙2q˙3 =21 0ωxωyωz−ωx0−ωzωy−ωyωz0−ωx−ωz−ωyωx0 q0q1q2q3
或者也可以写成如下形式:
d Q d t = 1 2 M ( Q ) ω n b b \frac{d \pmb{Q}}{d t}=\frac{1}{2} M(\pmb{Q}) \omega_{n b}^{b} \\ dtdQ=21M(Q)ωnbb
即为:
[ q ˙ 0 q ˙ 1 q ˙ 2 q ˙ 3 ] = 1 2 [ q 0 − q 1 − q 2 − q 3 q 1 q 0 − q 3 q 2 q 2 q 3 q 0 − q 1 q 3 − q 2 q 1 q 0 ] [ 0 ω x ω y ω z ] \left[\begin{array}{l} {\dot{q}_{0}} \\ {\dot{q}_{1}} \\ {\dot{q}_{2}} \\ {\dot{q}_{3}} \end{array}\right]=\frac{1}{2}\left[\begin{array}{cccc} {q_{0}} & {-q_{1}} & {-q_{2}} & {-q_{3}} \\ {q_{1}} & {q_{0}} & {-q_{3}} & {q_{2}} \\ {q_{2}} & {q_{3}} & {q_{0}} & {-q_{1}} \\ {q_{3}} & {-q_{2}} & {q_{1}} & {q_{0}} \end{array}\right]\left[\begin{array}{c} {0} \\ {\omega_{x}} \\ {\omega_{y}} \\ {\omega_{z}} \end{array}\right] \\ q˙0q˙1q˙2q˙3 =21 q0q1q2q3−q1q0q3−q2−q2−q3q0q1−q3q2−q1q0 0ωxωyωz
此处,我们采用第一种表达方式: d Q d t = 1 2 M ′ ( ω n b b ) Q \frac{d \pmb{Q}}{d t}=\frac{1}{2} M^{\prime}\left(\omega_{n b}^{b}\right) \pmb{Q} dtdQ=21M′(ωnbb)Q
注意:四元数乘法不满足交换律
P ⊗ Q = M ( P ) Q = M ′ ( Q ) P \pmb{P} \otimes \pmb{Q}=\pmb{M(P)Q}=\pmb{M^{'}(Q)P} P⊗Q=M(P)Q=M′(Q)P
P ⊗ Q = M ( P ) Q ≠ M ′ ( P ) Q = Q ⊗ P \pmb{P} \otimes \pmb{Q}=\pmb{M(P)Q}\neq\pmb{M^{'}(P)Q}=\pmb{Q} \otimes \pmb{P} P⊗Q=M(P)Q=M′(P)Q=Q⊗P
四元数乘法满足分配律与结合律:
P ⊗ ( Q + R ) = P ⊗ Q + P ⊗ R \pmb{P} \otimes (\pmb{Q}+\pmb{R})=\pmb{P} \otimes \pmb{Q}+\pmb{P} \otimes\pmb{R} P⊗(Q+R)=P⊗Q+P⊗R
P ⊗ Q ⊗ R = ( P ⊗ Q ) ⊗ R = P ⊗ ( Q ⊗ R ) \pmb{P} \otimes \pmb{Q}\otimes\pmb{R}=(\pmb{P} \otimes \pmb{Q})\otimes\pmb{R}=\pmb{P} \otimes (\pmb{Q}\otimes\pmb{R}) P⊗Q⊗R=(P⊗Q)⊗R=P⊗(Q⊗R)
3.3 龙格-库塔法求解微分方程
由 上一节 3.2可知 d Q d t \frac{d \pmb{Q}}{d t} dtdQ如下所示:
d Q d t = 1 2 M ′ ( ω n b b ) Q \frac{d \pmb{Q}}{d t}=\frac{1}{2} M^{\prime}\left(\omega_{n b}^{b}\right) \pmb{Q} \\ dtdQ=21M′(ωnbb)Q
即
[ q ˙ 0 q ˙ 1 q ˙ 2 q ˙ 3 ] = 1 2 [ 0 − ω x − ω y − ω z ω x 0 ω z − ω y ω y − ω z 0 ω x ω z ω y − ω x 0 ] [ q 0 q 1 q 2 q 3 ] \left[\begin{array}{c} {\dot{q}_{0}} \\ {\dot{q}_{1}} \\ {\dot{q}_{2}} \\ {\dot{q}_{3}} \end{array}\right]=\frac{1}{2}\left[\begin{array}{cccc} {0} & {-\omega_{x}} & {-\omega_{y}} & {-\omega_{z}} \\ {\omega_{x}} & {0} & {\omega_{z}} & {-\omega_{y}} \\ {\omega_{y}} & {-\omega_{z}} & {0} & {\omega_{x}} \\ {\omega_{z}} & {\omega_{y}} & {-\omega_{x}} & {0} \end{array}\right]\left[\begin{array}{l} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right] \\ q˙0q˙1q˙2q˙3 =21 0ωxωyωz−ωx0−ωzωy−ωyωz0−ωx−ωz−ωyωx0 q0q1q2q3
龙格库塔法(Runge-Kutta,简称RK法)是一组常微分方程求解器,它可以根据要求调整阶数,输出误差级别不一样的结果。龙格库塔法的基本思想囊括了欧拉法、显式梯形法、中点法和泰勒法,是一种使用广泛的求解方法(具体可参考参考链接)。
龙格库塔法的一般形式
龙格库塔法通过在区间内取多个点的斜率,然后进行线性组合,从而得到不用计算高阶导数的n阶方法。它的一般形式如下:
{ ω 0 = y 0 w i + 1 = w i + h ∑ i = 1 L λ i K i K 1 = f ( x i , w i ) K i = f ( x n + c i h , w i + c i h ∑ j = 1 i − 1 a i j K i ) , i = 2 , 3 , … , L \begin{cases} ω_0 = y_0 \\ w_{i+1} = w_i+h\sum^L_{i=1}\lambda_iK_i \\ K_1=f(x_i, w_i) \\ K_i = f(x_n+c_ih,w_i+c_ih\sum^{i-1}_{j=1}a_{ij}K_i) & ,i=2,3,\dots,L \end{cases} ⎩ ⎨ ⎧ω0=y0wi+1=wi+h∑i=1LλiKiK1=f(xi,wi)Ki=f(xn+cih,wi+cih∑j=1i−1aijKi),i=2,3,…,L
其中, c i ≤ 1 , ∑ i = 1 L λ i = 1 , ∑ j = 1 i − 1 a i j = 1 c_i\le1, \sum^L_{i=1}\lambda_i=1, \sum_{j=1}^{i-1}a_{ij}=1 ci≤1,∑i=1Lλi=1,∑j=1i−1aij=1 。
可知,此处使用一阶龙格-库塔法,则 L = 1 , h = d t L=1, h=dt L=1,h=dt
K 1 = f ( x i , w i ) = 1 2 [ 0 − ω x − ω y − ω z ω x 0 ω z − ω y ω y − ω z 0 ω x ω z ω y − ω x 0 ] [ q 0 q 1 q 2 q 3 ] K_1=f(x_i, w_i)=\frac{1}{2}\left[\begin{array}{cccc} {0} & {-\omega_{x}} & {-\omega_{y}} & {-\omega_{z}} \\ {\omega_{x}} & {0} & {\omega_{z}} & {-\omega_{y}} \\ {\omega_{y}} & {-\omega_{z}} & {0} & {\omega_{x}} \\ {\omega_{z}} & {\omega_{y}} & {-\omega_{x}} & {0} \end{array}\right]\left[\begin{array}{l} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right] K1=f(xi,wi)=21 0ωxωyωz−ωx0−ωzωy−ωyωz0−ωx−ωz−ωyωx0 q0q1q2q3
Q i + 1 = Q i + d t K i = Q i + 1 2 [ 0 − ω x − ω y − ω z ω x 0 ω z − ω y ω y − ω z 0 ω x ω z ω y − ω x 0 ] [ q 0 q 1 q 2 q 3 ] d t \pmb{Q}_{i+1} = \pmb{Q}_{i}+dtK_i=\pmb{Q}_{i}+\frac{1}{2}\left[\begin{array}{cccc} {0} & {-\omega_{x}} & {-\omega_{y}} & {-\omega_{z}} \\ {\omega_{x}} & {0} & {\omega_{z}} & {-\omega_{y}} \\ {\omega_{y}} & {-\omega_{z}} & {0} & {\omega_{x}} \\ {\omega_{z}} & {\omega_{y}} & {-\omega_{x}} & {0} \end{array}\right]\left[\begin{array}{l} {q_{0}} \\ {q_{1}} \\ {q_{2}} \\ {q_{3}} \end{array}\right]dt Qi+1=Qi+dtKi=Qi+21 0ωxωyωz−ωx0−ωzωy−ωyωz0−ωx−ωz−ωyωx0 q0q1q2q3 dt
四、Mahony 互补滤波
在进行软件姿态解算中,传入数据参数是陀螺仪x,y,z值、加速度计x,y,z值,磁力计x,y,z值及两帧数据时间差dt,首先把加速度计采集到的值(三维向量)转化为单位向量,即向量除以模:
void NonlinearSO3AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz, float twoKp, float twoKi, float dt)//归一化,得到单位加速度
recipNorm = invSqrt(ax * ax + ay * ay + az * az); // 求平方根的倒数
ax *= recipNorm;
ay *= recipNorm;
az *= recipNorm;
把机器人上次计算得到的姿态(四元数)换算成“方向余弦矩阵”中的第三行的三个元素。根据余弦矩阵和欧拉角的定义,将世界坐标系的重力向量转到机体坐标系,正好是这三个元素。所以这里的halfvx、halfvy、halfvz,其实是用上一次机器人机体姿态(四元数)换算出来的在当前的机体坐标系上的重力单位向量。注意,代码中取了其中的一半1/2,下面的误差同理。
// 根据余弦矩阵和欧拉角将地理坐标系转至机体坐标系(用上一时刻goat的姿态四元数换算到当前机体坐标系的重力单位向量)
// 即 陀螺仪积分后推算的重力分量halfvx = q1q3 - q0q2; // 使用 halfvx 而非 vx 是为了减小乘法运算量
halfvy = q0q1 + q2q3;
halfvz = q0q0 - 0.5f + q3q3; // ! 为什么直接是0.5f: q0q0 - q1q1 - q2q2 + q3q3 = q0q0 - q1q1 - q2q2 + q3q3 + 1 - 1axyz是机体坐标参照系上,加速度计测出来的重力向量,也就是实际测出来的重力向量。axyz是测量得到的重力向量,halfvxyz是陀螺积分后的姿态来推算出的重力向量,它们都是机体坐标参照系上的重力向量。那它们之间的误差向量,就是陀螺积分后的姿态和加计测出来的姿态之间的误差。向量间的误差,可以用向量叉积(也叫向量外积、叉乘)来表示,halfexyz就是两个重力向量的叉积。这个叉积向量仍旧是位于机体坐标系上的,而陀螺积分误差也是在机体坐标系,而且叉积的大小与陀螺积分误差成正比,正好拿来纠正陀螺仪。(你可以自己拿东西想象一下)由于陀螺是对机体直接积分,所以对陀螺的纠正量会直接体现在对机体坐标系的纠正。
// 获得叉积误差,叉积的大小与陀螺仪积分误差成正比
// Err = 单位加速度a X(叉乘) 积分重力分量v
halfex += ay * halfvz - az * halfvy;
halfey += az * halfvx - ax * halfvz;
halfez += ax * halfvy - ay * halfvx;
下面一段代码,用叉乘误差来做 K p K_p Kp、 K i K_i Ki修正陀螺零偏,通过调节twoKp,twoKi两个参数,可以控制加速度计修正陀螺仪积分姿态的速度。
// 叉积误差判断if(halfex != 0.0f && halfey != 0.0f && halfez != 0.0f) {// 用叉积误差进行积分// 通过 twoKp 、twoKi 比例、积分参数控制加速计修正陀螺仪积分姿态的速度// w_bias = Kp*Err + Ki*\sumErrif(twoKi > 0.0f) {gyro_bias[0] += twoKi * halfex * dt; // 误差积分gyro_bias[1] += twoKi * halfey * dt;gyro_bias[2] += twoKi * halfez * dt;// 积分反馈gx += gyro_bias[0];gy += gyro_bias[1];gz += gyro_bias[2];}else {gyro_bias[0] = 0.0f; // 防止积分饱和gyro_bias[1] = 0.0f;gyro_bias[2] = 0.0f;}// 比例反馈gx += twoKp * halfex; gy += twoKp * halfey;gz += twoKp * halfez;}
到此,使用加速度计数据对陀螺仪数据的修正已经完成,这就是姿态解算中的深度融合。
接着,将修正后的陀螺仪数据通过四元数微分方程更新至当前姿态角中。
// 四元数微分方程(一阶龙格-库塔法).// |dq0| | 0 -gx -gy -gz||q0|// |dq1| | gx 0 gz -gy||q1|// s1 = |dq2| = 0.5*| gy -gz 0 gx||q2| // |dq3| | gz gy -gx 0 ||q3|dq0 = 0.5f*(-q1 * gx - q2 * gy - q3 * gz);dq1 = 0.5f*(q0 * gx + q2 * gz - q3 * gy); dq2 = 0.5f*(q0 * gy - q1 * gz + q3 * gx);dq3 = 0.5f*(q0 * gz + q1 * gy - q2 * gx);// q_i+1 = q_i + s1*dtq0 += dt*dq0;q1 += dt*dq1;q2 += dt*dq2;q3 += dt*dq3;
整理的整个流程如下图所示,如有错误,敬请指正,谢谢!!

附录
四元数乘法法则容易推出 n ^ ⊗ n ^ = − 1 \hat{n} \otimes \hat{n}=-1 n^⊗n^=−1
p ⊗ q = [ p w q w − p v T q v p w q v + q w p v + p v × q v ] \mathrm{p} \otimes \mathrm{q}=\left[\begin{array}{c} {p_{w} q_{w}-p_{v}^{T} q_{v}} \\ {p_{w} q_{v}+q_{w} p_{v}+p_{v} \times q_{v}} \end{array}\right] \\ p⊗q=[pwqw−pvTqvpwqv+qwpv+pv×qv]
其中 w w w 代表实部, υ υ υ 代表虚部, p v T p_{v}^{T} pvT为 p v p_{v} pv的转置,当 p p p 和 q q q 为纯四元数时,
p ⊗ q = [ − p v T q v p v × q v ] \mathrm{p} \otimes \mathrm{q}=\left[\begin{array}{l} {-p_{v}^{T} q_{v}} \\ {p_{v} \times q_{v}} \end{array}\right] \\ p⊗q=[−pvTqvpv×qv]
p ⊗ p = − p v T p v = − ∥ p v ∥ 2 = − 1 \mathrm{p} \otimes \mathrm{p}=-p_{v}^{T} p_{v}=-\left\|p_{v}\right\|^{2}=-1 \\ p⊗p=−pvTpv=−∥pv∥2=−1
相关完整代码如下:
// 描述:姿态解算器初始化
static void NonlinearSO3AHRSinit(float ax, float ay, float az, float mx, float my, float mz)
{float initialRoll, initialPitch;float cosRoll, sinRoll, cosPitch, sinPitch;float magX, magY;float initialHdg, cosHeading, sinHeading;initialRoll = atan2(-ay, -az);initialPitch = atan2(ax, -az);cosRoll = cosf(initialRoll);sinRoll = sinf(initialRoll);cosPitch = cosf(initialPitch);sinPitch = sinf(initialPitch);magX = mx * cosPitch + my * sinRoll * sinPitch + mz * cosRoll * sinPitch;magY = my * cosRoll - mz * sinRoll;initialHdg = atan2f(-magY, magX);cosRoll = cosf(initialRoll * 0.5f);sinRoll = sinf(initialRoll * 0.5f);cosPitch = cosf(initialPitch * 0.5f);sinPitch = sinf(initialPitch * 0.5f);cosHeading = cosf(initialHdg * 0.5f);sinHeading = sinf(initialHdg * 0.5f);q0 = cosRoll * cosPitch * cosHeading + sinRoll * sinPitch * sinHeading;q1 = sinRoll * cosPitch * cosHeading - cosRoll * sinPitch * sinHeading;q2 = cosRoll * sinPitch * cosHeading + sinRoll * cosPitch * sinHeading;q3 = cosRoll * cosPitch * sinHeading - sinRoll * sinPitch * cosHeading;// 辅助变量,避免重复操作q0q0 = q0 * q0;q0q1 = q0 * q1;q0q2 = q0 * q2;q0q3 = q0 * q3;q1q1 = q1 * q1;q1q2 = q1 * q2;q1q3 = q1 * q3;q2q2 = q2 * q2;q2q3 = q2 * q3;q3q3 = q3 * q3;
}// 函数名:NonlinearSO3AHRSupdate()
// 描述:姿态解算融合, Mahony互补滤波算法
// 说明:陀螺仪具有良好高频特性,但会随着时间漂移; 加速计具有良好低频特性,不会随着时间漂移,但goat剧烈运动,不易解算真实姿态
// static void NonlinearSO3AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz, float twoKp, float twoKi, float dt)
void NonlinearSO3AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz, float twoKp, float twoKi, float dt){float recipNorm;float halfex = 0.0f, halfey = 0.0f, halfez = 0.0f;// 初始化条件,静置初始化 (注意,避免抱起机器在空中进行重启)if(bFilterInit == 0) {NonlinearSO3AHRSinit(ax,ay,az,mx,my,mz);bFilterInit = 1;}// 若存在磁力计数据,则使用磁力计数据if(!((mx == 0.0f) && (my == 0.0f) && (mz == 0.0f))) {float hx, hy, hz, bx, bz;float halfwx, halfwy, halfwz;recipNorm = invSqrt(mx * mx + my * my + mz * mz); // 求平方根的倒数mx *= recipNorm;my *= recipNorm;mz *= recipNorm;hx = 2.0f * (mx * (0.5f - q2q2 - q3q3) + my * (q1q2 - q0q3) + mz * (q1q3 + q0q2));hy = 2.0f * (mx * (q1q2 + q0q3) + my * (0.5f - q1q1 - q3q3) + mz * (q2q3 - q0q1));hz = 2.0f * mx * (q1q3 - q0q2) + 2.0f * my * (q2q3 + q0q1) + 2.0f * mz * (0.5f - q1q1 - q2q2);bx = sqrt(hx * hx + hy * hy);bz = hz;halfwx = bx * (0.5f - q2q2 - q3q3) + bz * (q1q3 - q0q2);halfwy = bx * (q1q2 - q0q3) + bz * (q0q1 + q2q3);halfwz = bx * (q0q2 + q1q3) + bz * (0.5f - q1q1 - q2q2);halfex += (my * halfwz - mz * halfwy);halfey += (mz * halfwx - mx * halfwz);halfez += (mx * halfwy - my * halfwx);}if(!((ax == 0.0f) && (ay == 0.0f) && (az == 0.0f))){float halfvx, halfvy, halfvz;//归一化,得到单位加速度recipNorm = invSqrt(ax * ax + ay * ay + az * az); // 求平方根的倒数ax *= recipNorm;ay *= recipNorm;az *= recipNorm;// 根据余弦矩阵和欧拉角将地理坐标系转至机体坐标系(用上一时刻goat的姿态四元数换算到当前机体坐标系的重力单位向量)// 即 陀螺仪积分后推算的重力分量halfvx = q1q3 - q0q2; // 使用 halfvx 而非 vx 是为了减小乘法运算量halfvy = q0q1 + q2q3;halfvz = q0q0 - 0.5f + q3q3; // ! 为什么直接是0.5f: q0q0 - q1q1 - q2q2 + q3q3 = q0q0 - q1q1 - q2q2 + q3q3 + 1 - 1// 获得叉积误差,叉积的大小与陀螺仪积分误差成正比// Err = 单位加速度a X(叉乘) 积分重力分量vhalfex += ay * halfvz - az * halfvy;halfey += az * halfvx - ax * halfvz;halfez += ax * halfvy - ay * halfvx;}// 叉积误差判断if(halfex != 0.0f && halfey != 0.0f && halfez != 0.0f) {// 用叉积误差进行积分// 通过 twoKp 、twoKi 比例、积分参数控制加速计修正陀螺仪积分姿态的速度// w_bias = Kp*Err + Ki*\sumErrif(twoKi > 0.0f) {gyro_bias[0] += twoKi * halfex * dt; // 误差积分gyro_bias[1] += twoKi * halfey * dt;gyro_bias[2] += twoKi * halfez * dt;// 积分反馈gx += gyro_bias[0];gy += gyro_bias[1];gz += gyro_bias[2];}else {gyro_bias[0] = 0.0f; // 防止积分饱和gyro_bias[1] = 0.0f;gyro_bias[2] = 0.0f;}// 比例反馈gx += twoKp * halfex; gy += twoKp * halfey;gz += twoKp * halfez;}// 四元数微分方程(一阶龙格-库塔法).//! \dot{q} = 0.5*q \otimes P(\omega)// |dq0| | 0 -gx -gy -gz||q0|// |dq1| | gx 0 gz -gy||q1|// s1 = |dq2| = 0.5*| gy -gz 0 gx||q2| // |dq3| | gz gy -gx 0 ||q3|dq0 = 0.5f*(-q1 * gx - q2 * gy - q3 * gz);dq1 = 0.5f*(q0 * gx + q2 * gz - q3 * gy); dq2 = 0.5f*(q0 * gy - q1 * gz + q3 * gx);dq3 = 0.5f*(q0 * gz + q1 * gy - q2 * gx);// q_i+1 = q_i + s1*dtq0 += dt*dq0;q1 += dt*dq1;q2 += dt*dq2;q3 += dt*dq3;// 四元数归一化recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3); // 求平方根的倒数if(recipNorm!=0){q0 *= recipNorm;q1 *= recipNorm;q2 *= recipNorm;q3 *= recipNorm;Quaternion.Q[0] = q0;Quaternion.Q[1] = q1;Quaternion.Q[2] = q2;Quaternion.Q[3] = q3;// 辅助变量,避免重复计算q0q0 = q0 * q0;q0q1 = q0 * q1;q0q2 = q0 * q2;q0q3 = q0 * q3;q1q1 = q1 * q1;q1q2 = q1 * q2;q1q3 = q1 * q3;q2q2 = q2 * q2;q2q3 = q2 * q3;q3q3 = q3 * q3;}
}