459. 重复的子字符串
- 原题链接:
- 完成情况:
- 解题思路:
- 参考代码:
- __459重复的子字符串_枚举
- __459重复的子字符串_字符串匹配
- __459重复的子字符串_KMP算法
- __459重复的子字符串_优化的KMP算法
- 错误经验吸取
原题链接:
459. 重复的子字符串
https://leetcode.cn/problems/repeated-substring-pattern/submissions/
完成情况:
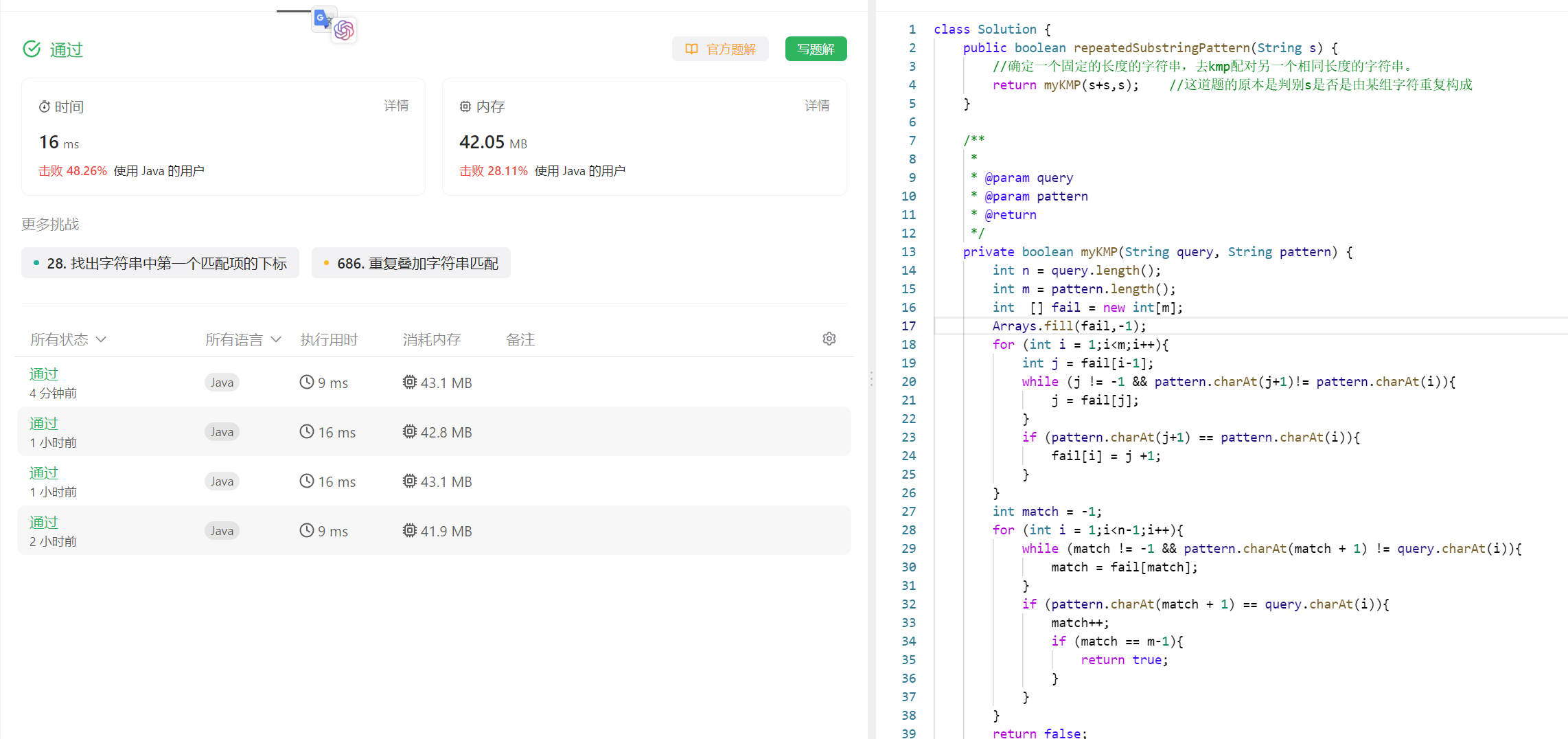
解题思路:
思路与算法如果一个长度为 nnn 的字符串 sss 可以由它的一个长度为 n′n'n
′的子串 s′s's
′重复多次构成,那么:nnn 一定是 n′n'n
′的倍数;s′s's
′一定是 sss 的前缀;对于任意的 i∈[n′,n)i \in [n', n)i∈[n
′,n),有 s[i]=s[i−n′]s[i] = s[i-n']s[i]=s[i−n
′]。也就是说,sss 中长度为 n′n'n
′的前缀就是 s′s's
′,并且在这之后的每一个位置上的字符 s[i]s[i]s[i],都需要与它之前的第 n′n'n
′个字符 s[i−n′]s[i-n']s[i−n
′] 相同。因此,我们可以从小到大枚举 n′n'n
′,并对字符串 sss 进行遍历,进行上述的判断。注意到一个小优化是,因为子串至少需要重复一次,所以 n′n'n
′不会大于 nnn 的一半,我们只需要在 [1,n2][1, \frac{n}{2}][1,
2
n
] 的范围内枚举 n′n'n
′即可。参考代码:
__459重复的子字符串_枚举
package 代码随想录.字符串;public class __459重复的子字符串_枚举 {//给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。/**方法一: 双重for循环,其中一个for循环,用i,j记录起始,截止位置;;另一个for循环,用于剩余的j到结尾。*/public boolean repeatedSubstringPattern(String s) {/*提示:1 <= s.length <= 104s 由小写英文字母组成解法1:调用KMP算法/暴力for循环?,将一个部分,分成从[0,i]和[i+1,s.length-1]的两个子串。*/int n = s.length();for (int i = 1;i*2 <= n;i++){ //要能够匹配,最多只能遍历一般即可。if (n % i == 0){ //把i作为匹配对象boolean match = true;for (int j = i;j < n;j++){ //j是匹配位置if (s.charAt(j)!= s.charAt(j-i)){ //同步j-i位置。【i为配对对象】match = false;break;}}if (match){return true;}}}return false;}
}__459重复的子字符串_字符串匹配
package 代码随想录.字符串;public class __459重复的子字符串_字符串匹配 {/*** 调用方法进行配对** @param s* @return*/public boolean repeatedSubstringPattern(String s){return (s+s).indexOf(s,1) != s.length();}
}__459重复的子字符串_KMP算法
package 代码随想录.字符串;import java.util.Arrays;public class __459重复的子字符串_KMP算法 {public boolean repeatedSubstringPattern(String s) {//确定一个固定的长度的字符串,去kmp配对另一个相同长度的字符串。return myKMP(s+s,s); //这道题的原本是判别s是否是由某组字符重复构成}/**** @param query* @param pattern* @return*/private boolean myKMP(String query, String pattern) {int n = query.length();int m = pattern.length();int [] fail = new int[m];Arrays.fill(fail,-1);for (int i = 1;i<m;i++){int j = fail[i-1];while (j != -1 && pattern.charAt(j+1)!= pattern.charAt(i)){j = fail[j];}if (pattern.charAt(j+1) == pattern.charAt(i)){fail[i] = j +1;}}int match = -1;for (int i = 1;i<n-1;i++){while (match != -1 && pattern.charAt(match + 1) != query.charAt(i)){match = fail[match];}if (pattern.charAt(match + 1) == query.charAt(i)){match++;if (match == m-1){return true;}}}return false;}
}__459重复的子字符串_优化的KMP算法
package 代码随想录.字符串;import java.util.Arrays;public class __459重复的子字符串_优化的KMP算法 {public boolean repeatedSubstringPattern(String s) {//确定一个固定的长度的字符串,去kmp配对另一个相同长度的字符串。return myKMP(s); //这道题的原本是判别s是否是由某组字符重复构成}/**** @param pattern* @return*/private boolean myKMP(String pattern) {int n = pattern.length();int [] fail = new int[n];Arrays.fill(fail,-1);for (int i = 1;i<n;i++) {int j = fail[i-1];while (j!= -1 && pattern.charAt(j+1)!= pattern.charAt(i)){j = fail[j];}if (pattern.charAt(j+1) == pattern.charAt(i)){fail[i] = j +1;}}return fail[n-1] != -1 && n%(n- fail[n-1] - 1) == 0 ;}}