优质博文:IT-BLOG-CN
一、题目
给你二叉树的根节点root和一个表示目标和的整数targetSum。判断该树中是否存在 根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和targetSum。如果存在,返回true;否则,返回false。
叶子节点是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
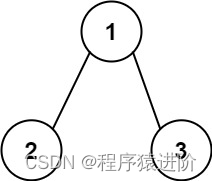
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:(1 --> 2): 和为3,(1 --> 3): 和为4不存在sum = 5的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
:::warning
树中节点的数目在范围[0, 5000]内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
:::
二、代码
【1】广度优先搜索: 通过广度优先搜索创建两个队列,记录横向节点和从根节点到当前节点的路径和。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) {return false;}// 使用广度优先方法:创建两个队列,一个存放横向的val值,一个存放与root节点线路的sum值Queue<TreeNode> values = new LinkedList<TreeNode>();Queue<Integer> sums = new LinkedList<Integer>();values.offer(root);sums.offer(root.val);while (!values.isEmpty()) {// 目的获取当前节点的左右子树TreeNode currentTree = values.poll();Integer temp = sums.poll();if (currentTree.left == null && currentTree.right == null) {if (temp == targetSum) {return true;}continue;}// 如果不为空,这将左右子树放入队列中if (currentTree.left != null) {values.offer(currentTree.left);sums.offer(currentTree.left.val + temp);}if (currentTree.right != null) {values.offer(currentTree.right);sums.offer(currentTree.right.val + temp);}}return false;}
}
时间复杂度: O(N)其中N是树的节点数。对每个节点访问一次。
空间复杂度: O(N)其中N是树的节点数。空间复杂度主要取决于队列的开销,队列中的元素个数不会超过树的节点数。
【2】递归: 假定从根节点到当前节点的值之和为val,我们可以将这个大问题转化为一个小问题:是否存在从当前节点的子节点到叶子的路径,满足其路径和为sum - val。不难发现这满足递归的性质,若当前节点就是叶子节点,那么我们直接判断sum是否等于val即可(因为路径和已经确定,就是当前节点的值,我们只需要判断该路径和是否满足条件)。若当前节点不是叶子节点,我们只需要递归地询问它的子节点是否能满足条件即可。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) {return false;}if (root.left == null && root.right == null) {return root.val == targetSum;}return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);}
}
时间复杂度: O(N)其中N是树的节点数。对每个节点访问一次。
空间复杂度: O(H)其中H是树的高度。空间复杂度主要取决于递归时栈空间的开销,最坏情况下,树呈现链状,空间复杂度为O(N)。平均情况下树的高度与节点数的对数正相关,空间复杂度为O(logN)。