Count-based exploration with neural density models[J]. International Conference on Machine Learning,International Conference on Machine Learning, 2017.
基于计数的神经密度模型探索
0、问题
这篇文章的关键在于弄懂pseudo-count的概念,以及是如何运用pseudo-count去进行探索的。pseudo-count主要用于生成探索奖励,即可以理解为生成内在奖励。
但是仍然保留一个疑问为在使用PixelCNN得到状态st的概率密度和状态st+1的概率密度后,为何不适用
N ^ n ( x ) = ρ n ( x ) ( 1 − ρ n ′ ( x ) ) ρ n ′ ( x ) − ρ n ( x ) \hat{\mathrm{N}}_n(x)=\frac{\rho_n(x)(1-\rho_n'(x))}{\rho_n'(x)-\rho_n(x)} N^n(x)=ρn′(x)−ρn(x)ρn(x)(1−ρn′(x))
这一公式来直接计算pseudo-count,这里的计算好像还用的是等号?而使用
N ^ n ( x ) ≈ ( e P G n ( x ) − 1 ) − 1 \hat{\mathrm{N}}_n(x)\approx\left(e^{\mathrm{PG}_n(x)}-1\right)^{-1} N^n(x)≈(ePGn(x)−1)−1
这一公式来近似计算pseudo-count?
1、Motivation
本文主要是针对强化学习中的智能体探索方面,提出了一种基于计数的探索方式。
在强化学习中,dynamics(动态模型)指的是对环境的模拟或建模。它描述了智能体与环境互动的方式,包括智能体采取行动后环境如何变化以及智能体所观察到的状态转换。
“pseudo-count”(伪计数)是一个在统计学和机器学习中常用的概念。它指的是一种人为引入的计数,用于对现有数据的不确定性进行建模。
密度模型(Density Model)是一种用于建模概率密度函数的数学模型,它可以用来描述或预测随机变量的分布。密度模型在统计学、概率论、信息论、机器学习等领域中得到了广泛应用。
2、Background
状态的概率密度模型p
ρ ( x ) = P ( X n + 1 = x ∣ X 1 … X n = x 1 : n ) = N ^ ( x ) n ^ \rho(x)=P(X_{n+1}=x|X_1\ldots X_n=x_{1:n})=\frac{\hat{N}(x)}{\hat{n}} ρ(x)=P(Xn+1=x∣X1…Xn=x1:n)=n^N^(x)
prediction gain of ρ:
P G n ( x ) = log ρ n ′ ( x ) − log ρ n ( x ) \mathrm{PG}_n(x)=\log\rho_n^{\prime}(x)-\log\rho_n(x) PGn(x)=logρn′(x)−logρn(x)
pseudo-count:
- N ^ n ( x ) = ρ n ( x ) ( 1 − ρ n ′ ( x ) ) ρ n ′ ( x ) − ρ n ( x ) \hat{\mathrm{N}}_n(x)=\frac{\rho_n(x)(1-\rho_n'(x))}{\rho_n'(x)-\rho_n(x)} N^n(x)=ρn′(x)−ρn(x)ρn(x)(1−ρn′(x))
pseudo-count可以用PG来近似:
N ^ n ( x ) ≈ ( e P G n ( x ) − 1 ) − 1 \hat{\mathrm{N}}_n(x)\approx\left(e^{\mathrm{PG}_n(x)}-1\right)^{-1} N^n(x)≈(ePGn(x)−1)−1
tips:以上公式的具体推导引用了白辰甲老师的知乎回答强化学习中的探索与利用(count-based) - 知乎 (zhihu.com)
由此可以得到这篇文章中提出的内在奖励公式:
r + ( x ) : = ( N ^ n ( x ) ) − 1 / 2 r^+(x):=(\hat{\mathrm{N}}_n(x))^{-1/2} r+(x):=(N^n(x))−1/2
本文估计期望回报采用mixed Monte-Carlo update (MMC)算法:
Q ( x , a ) ← Q ( x , a ) + α [ ( 1 − β ) δ ( x , a ) + β δ M C ( x , a ) ] Q(x,a)\leftarrow Q(x,a)+\alpha\left[(1-\beta)\delta(x,a)+\beta\delta_{\mathsf{MC}}(x,a)\right] Q(x,a)←Q(x,a)+α[(1−β)δ(x,a)+βδMC(x,a)]
其中:
δ ( x , a ) = r ( x , a ) + γ max a ′ Q ( x ′ , a ′ ) − Q ( x , a ) \delta\left(x,a\right)=r(x,a)+\gamma\operatorname*{max}_{a^{\prime}}Q(x^{\prime},a^{\prime})-Q(x,a) δ(x,a)=r(x,a)+γa′maxQ(x′,a′)−Q(x,a)
δ MC ( x , a ) = ∑ t = 0 ∞ γ t r ( x t , a t ) − Q ( x , a ) \delta_{\text{MC}}( x , a )=\begin{aligned}\sum_{t=0}^{\infty}\gamma^{t}r(x_{t},a_{t})-Q(x,a)\end{aligned} δMC(x,a)=t=0∑∞γtr(xt,at)−Q(x,a)
前者为TD算法中的目标值与实际值之差,后者为蒙特卡洛算法中实际回报与实际动作状态价值之差。
3、一些估计Return的算法
各种算法估计Return的利弊:
- TD(λ) with important sampling :可以保证收敛,但是重要性采样的系数引入了极大的方差,导致算法的收敛过程不稳定。
- Q(λ) :忽略重要性采样系数,直接乘以λ,能保证方差小,但是只有在采样策略和目标策略接近时才可以保证收敛,不安全。
- Retrace算法:低方差(控制了重要性采样系数的大小)、安全性高(总是能“安全”地利用各种行为策略采样得到的样本,当behavior policy和target policy差很多的时候,依然能保障收敛性)、样本效率高(对reward的压缩性没有那么高),但是Retrace(λ)算法在学习时过于谨慎,可能无法充分利用探索奖励,因为在计算重要性采样比率时采样的数据会被截断,只有那些足够接近当前策略的状态-行为轨迹才会被保留。
估计Return的通用算子:
R Q ( x , a ) : = Q ( x , a ) + E μ [ ∑ t ≥ 0 γ t ( ∏ s = 1 t c s ) ( r t + γ E π Q ( x t + 1 , ⋅ ) − Q ( x t , a t ) ) ] \mathcal{R}Q(x,a):=Q(x,a)+\mathbb{E}_\mu\left[\sum_{t\geq0}\gamma^t(\prod_{s=1}^tc_s)(r_t+\gamma\mathbb{E}_\pi Q(x_{t+1},\cdot)-Q(x_t,a_t))\right] RQ(x,a):=Q(x,a)+Eμ[t≥0∑γt(s=1∏tcs)(rt+γEπQ(xt+1,⋅)−Q(xt,at))]
将TD(λ)、Q(λ)、Retrace等算法的不同归结为c_{s}的不同:
-
TD(λ) with import sampling:
c s = λ ⋅ π ( a s ∣ x s ) μ ( a s ∣ x s ) c_s=\lambda\cdot\frac{\pi(a_s|x_s)}{\mu(a_s|x_s)} cs=λ⋅μ(as∣xs)π(as∣xs) -
Q(λ):
c s = λ c_s=\lambda\ cs=λ -
Retrace(λ):
c s = λ ⋅ m i n ( 1 , π ( a s ∣ x s ) μ ( a s ∣ x s ) ) c_s=\lambda\cdot min{\left(1,\frac{\pi(a_s|x_s)}{\mu(a_s|x_s)}\right)} cs=λ⋅min(1,μ(as∣xs)π(as∣xs))
由于Retrace(λ)使用了在1处截断的Importance Sampling,方差得到了降低。同时,因为
min ( 1 , π ( a s ∣ x s ) μ ( a s ∣ x s ) ) ≥ π ( a s ∣ x s ) \min\left(1,\frac{\pi(a_s|x_s)}{\mu(a_s|x_s)}\right)\geq\pi(a_s|x_s) min(1,μ(as∣xs)π(as∣xs))≥π(as∣xs)
所以Retrace(λ)对回报的压缩幅度更弱(尤其是在两个policy接近时),从而提高了return的利用效率。
tips:对于Retrace(λ)算子的详细推导过程见【Typical RL 19】Retrace - 知乎 (zhihu.com)
4、方法过程
使用PixelCNN,将当前状态作为输入,输出对应状态的概率密度估计,通过对状态概率密度进行计数,计算出每个状态的探索奖励,即越少访问过的状态获得的奖励越高。这样,在选择下一个动作时,在智能体的策略中加入了探索奖励的权重,以鼓励更多地探索未知的状态,从而提高学习效率和收敛速度。
为了确保pseudo-counts与真实计数近似线性增长,PG应该以n^-1的速率衰减。于是将PG_{n}替换为c_{n}*PG_{n},其中c_{n}为:
c n = c n c_n=\frac{c}{\sqrt{n}} cn=nc
文章中通过实验确定c=0.1时结果最好。
由于当神经网络模型的优化器超过局部损失的最小值时,会出现负PG,因此需要给PG设定一个阈值为0,得到最终的伪计数公式为:
N ^ n ( x ) = ( exp ( c ⋅ n − 1 / 2 ⋅ ( PG n ( x ) ) + ) − 1 ) − 1 \begin{aligned}\hat{\mathrm{N}}_n(x)&=\left(\exp\left(c\cdot n^{-1/2}\cdot(\operatorname{PG}_n(x))_+\right)-1\right)^{-1}\end{aligned} N^n(x)=(exp(c⋅n−1/2⋅(PGn(x))+)−1)−1
因此最终得到的组合探索奖励为:
r t = r ( x , a ) + ( N ^ n ( x ) ) − 1 / 2 r_t=\begin{aligned}r(x,a)+(\hat{\text{N}}_{n}(x))^{-1/2}\end{aligned} rt=r(x,a)+(N^n(x))−1/2
总而言之,引入PixelCNN是为了计算PG,进而计算状态的伪计数,将伪计数转化为智能体的内在奖励
5、实验
1、文章通过实验表明探索奖励(exploration bonus)对智能体性能的影响比较均匀,可以在很多游戏中提高智能体的表现。特别是在Reactor-PixelCNN这个环境下,使用探索奖励的效果要比没有探索奖励的Reactor更好,表现为更高的样本利用效率。
2、文章还通过实验说明了在极度难以探索的游戏中,MMC和PixelCNN探索奖励的组合效果最好,两者相辅相成,加快了训练进展并促使智能体达到高性能水平。
3、文章说明了PixelCNN模型在估计探索奖励方面的有效性,这里与CTS模型进行了对比。
4、文章通过实验发现在一定范围内增加 PG scale 可以加快算法的探索速度,并在多次试验中获得记录峰值分数。但是增加 PG scale 也会导致一些问题。因为探索奖励是一个固定的值,如果过度注重探索奖励,可能会导致算法稳定性下降,从而影响长期性能。
6、结论
虽然目前的伪计数理论对密度模型提出了严格的要求,但文章证明PixelCNN可以在更简单和更一般的设置中使用,并且可以完全在线训练。它还被证明与值函数和基于策略的RL算法广泛兼容。
PixelCNN提高了基础RL算法的学习速度和稳定性。
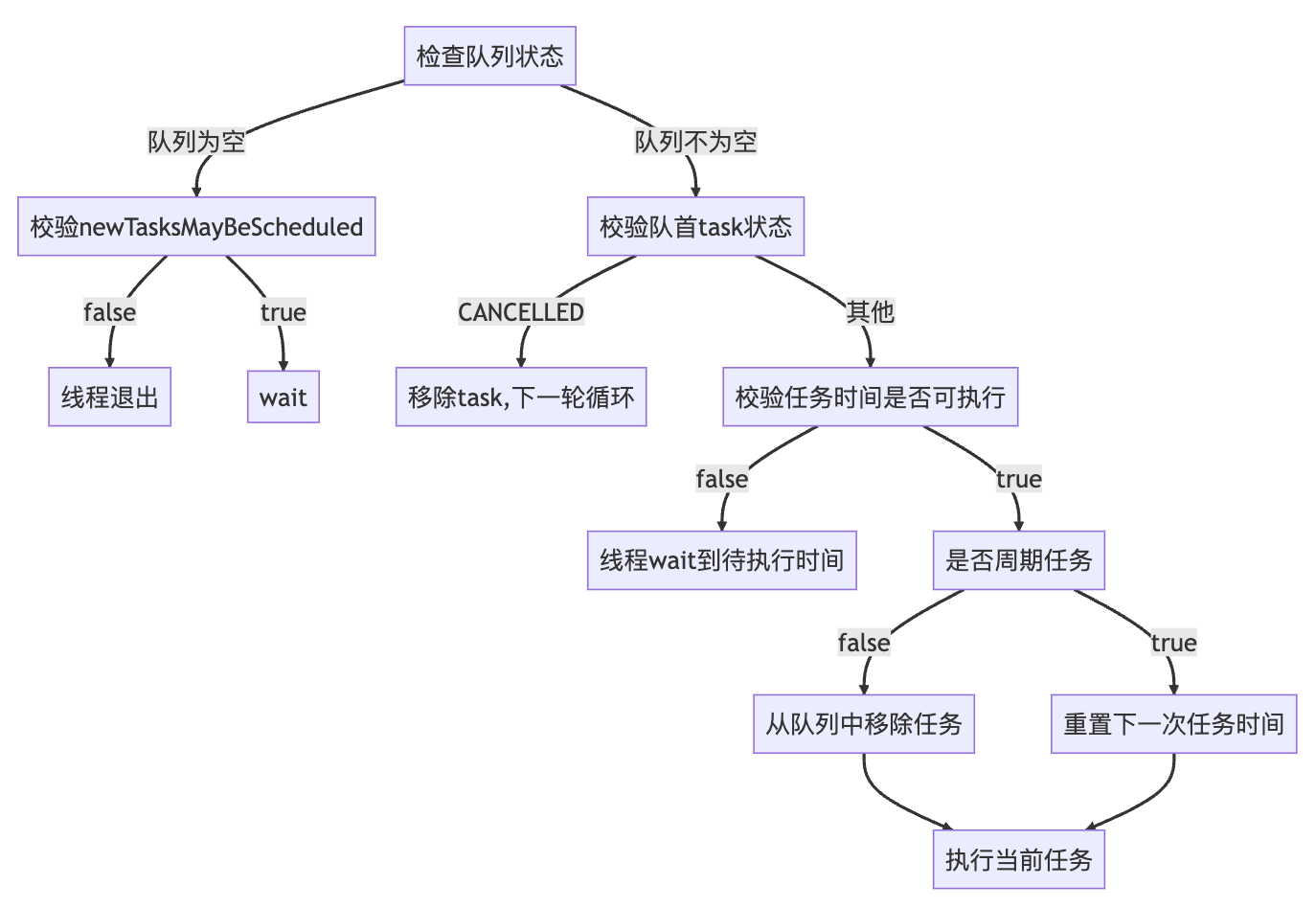
6、算法伪代码(以DQN为base)