离散时间系统模型
离散时间系统模型是表示数字滤波器的方案。MATLAB® 科学计算环境支持若干种离散时间系统模型,这些模型将在以下章节中介绍:
- 传递函数
- 零极点增益
- 状态空间
- 部分分式展开式(残差形式)
- 二阶节 (SOS)
- 格型结构体
- 卷积矩阵
传递函数
传递函数是数字滤波器的一种基本 Z 域表示,它将滤波器表示为两个多项式的比值。它是此工具箱的主要离散时间模型。数字滤波器的差分方程的 Z 变换的传递函数模型说明如下

此处,常量 b(i) 和 a(i) 是滤波器系数,滤波器的阶数是 n 和 m 的最大值。在 MATLAB 环境中,您将这些系数存储在两个向量中(按照惯例是行向量),一个行向量用于分子,一个行向量用于分母。有关传递函数形式的详细信息,请参阅滤波器和传递函数。
零极点增益
传递函数的分解形式(又称为零极点增益形式)为
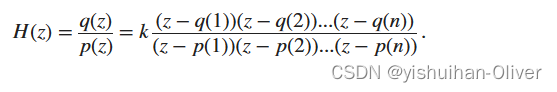
按照惯例,多项式系数存储在行向量中,多项式根存储在列向量中。因此,在零极点增益形式中,传递函数的分子和分母的零点和极点位置位于列向量中。分解传递函数增益 k 是 MATLAB 标量。
poly 和 roots 函数在多项式表示和零极点增益表示之间转换。例如,一个简单 IIR 滤波器如下
b = [2 3 4];
a = [1 3 3 1];此滤波器的零点和极点是
q = roots(b)
p = roots(a)
% Gain factor
k = b(1)/a(1)回到最初的多项式,
bb = k*poly(q)
aa = poly(p)请注意,本例中的 b 和 a 表示传递函数:
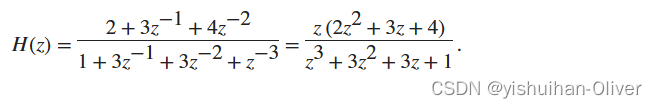
对于 b = [2 3 4],roots 函数会缺失 z 等于 0 时的零点。事实上,只要输入传递函数的极点数多于零点数(或相反),该函数都会缺失 z 等于 0 时的极点和零点。这在大多数情况下是可以接受的。然而,为了避免此问题,请在使用 roots 函数之前,直接追加零以使向量长度相同;
例如,b = [b 0]。
状态空间
将数字滤波器或差分方程组表示为一组一阶差分方程组始终是可能的。在矩阵或状态空间形式中,您可以将公式写为
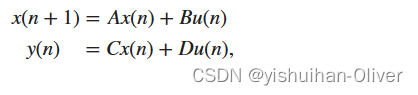 ,
,
其中 u 是输入,x 是状态向量,而 y 是输出。对于单通道系统,A 是 m×m 矩阵,其中 m 是滤波器的阶数,B 是列向量,C 是行向量,D 是标量。对于输入 u 和输出 y 成为向量、B、C 和 D 成为矩阵的多通道系统,状态空间表示法尤其方便。
状态空间表示很容易扩展到 MATLAB 环境。A、B、C 和 D 是矩形数组;MATLAB 函数将它们分别视为单个变量。
对状态空间方程进行 Z 变换并将其组合,表明状态空间形式和传递函数形式的等效性:
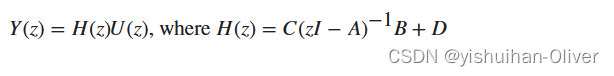
如果您不熟悉线性系统的状态空间表示,不要担心。一些滤波器设计算法在内部使用状态空间形式,但无需了解任何状态空间概念即可成功使用它们。不过,如果您的应用大量使用基于状态空间的信号处理,请了解 Control System Toolbox™ 产品,以获得全面的状态空间工具库。
部分分式展开式(残差形式)
每个传递函数还具有对应的部分分式展开(又称为残差形式),如下式所示

前提是 H(z) 没有重复的极点。此处,n 是有理传递函数 b(z)/a(z) 的分母多项式的次数。如果 r 是重极点 sr,则 H (z) 具有以下形式的项:

Signal Processing Toolbox™ 中的 residuez 函数用于将传递函数转换为部分分式展开式形式,或者反之。residuez 末尾的“z”表示 z 域或离散域。residuez 以列向量 p 形式返回极点,以列向量 r 形式返回极点对应的残差,以行向量 k 形式返回原始传递函数的任何不恰当部分。如果两个极点的差值的模小于任一极点的模的 0.1%,则 residuez 确定这两个极点相同。
部分分式展开式在信号处理中以一种求传递函数的逆 Z 变换的方法出现。例如,下式
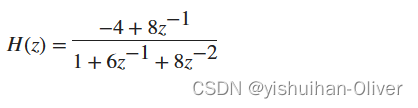
的部分分式展开式是
b = [-4 8];
a = [1 6 8];
[r,p,k] = residuez(b,a)它对应于

要想求出 H(z) 的逆 Z 变换,可以求 H(z) 的两个加数的逆 Z 变换之和,这可给出因果冲激响应:
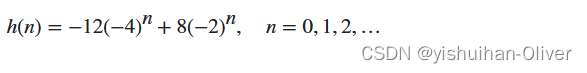
要在 MATLAB 环境中验证这一点,请键入
imp = [1 0 0 0 0];
resptf = filter(b,a,imp)
respres = filter(r(1),[1 -p(1)],imp)+...filter(r(2),[1 -p(2)],imp)二阶节 (SOS)
任何传递函数 H(z) 都有二阶节表示
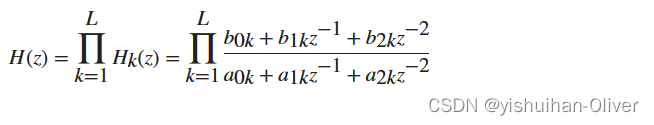
其中 L 是描述系统的二阶节的数量。MATLAB 环境将离散时间系统的二阶节形式表示为 L×6 数组 sos。sos 的每行包含一个二阶节,其中行元素是描述该二阶节的三个分子和三个分母系数。
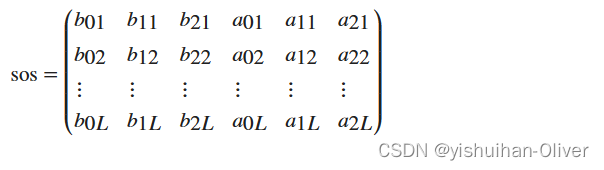
有许多方法以二阶节形式表示滤波器。通过仔细对极点和零点对组进行配对、对级联中的各节进行排序以及对各节进行乘性定标,可以在某些定点滤波器实现中降低量化噪声增益并避免溢出。Linear System Transformations 中所述的函数 zp2sos 和 ss2sos 用于执行零极点配对、节缩放和节排序。
注意
所有 Signal Processing Toolbox 二阶节变换仅适用于数字滤波器。
格型结构体
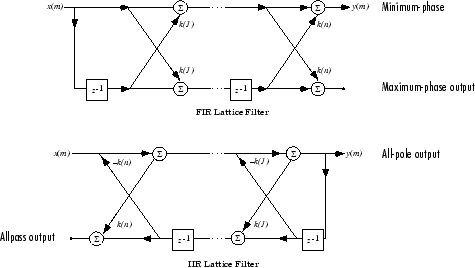
对于由多项式系数 a(n) 说明的离散的 N 阶全极点或全零滤波器,n = 1,2...,N+1,有 N 个对应的格型结构体系数 k (n),n = 1,2...,N。参数 k (n) 也称为滤波器的反射系数。给定这些反射系数,您可以实现如下所示的离散滤波器。
FIR 和 IIR 格型滤波器结构图
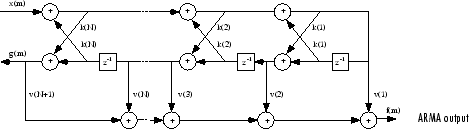
对于由多项式系数 a 和 b 说明的一般零极点 IIR 滤波器,分母 a 有格型系数 k (n),分子 b 有阶梯系数 v (n)。格型/梯形滤波器可以实现为
格型/梯形滤波器示意图
工具箱函数 tf2latc 接受多项式形式的 FIR 或 IIR 滤波器,并返回对应的反射系数。多项式形式的 FIR 滤波器的一个示例是
b = [1.0000 0.6149 0.9899 0.0000 0.0031 -0.0082];
此滤波器的格型(反射系数)表示为
k = tf2latc(b)
对于 IIR 滤波器,反射系数的幅值提供简单的稳定性检查。如果对应于一个多项式的所有反射系数的量级都小于 1,则该多项式的所有根都在单位圆内。例如,假设某 IIR 滤波器具有上述分子多项式 b 和如下的分母多项式:
a = [1 1/2 1/3];
则该滤波器的格型表示为
[k,v] = tf2latc(b,a);
对于 k 中的所有反射系数,abs(k) < 1,因此该滤波器是稳定的。
函数 latc2tf 根据滤波器的格型(反射)系数计算滤波器的多项式系数。给定反射系数向量 k,对应的多项式形式为
b = latc2tf(k);
格型或格型/梯形系数可用于使用函数 latcfilt 实现滤波器。
卷积矩阵
在信号处理中,对两个向量或矩阵求卷积等效于用一个输入操作数对另一个输入操作数进行滤波。这种关系支持将数字滤波器表示为卷积矩阵。
给定任意向量,工具箱函数 convmtx 生成一个矩阵,该矩阵与另一个向量的内积等于这两个向量的卷积。生成的矩阵表示一个数字滤波器,您可以将其应用于适当长度的任何向量;操作数的内部维度必须一致才能计算内积。
表示数字滤波器分子系数的向量 b 的卷积矩阵为
b = [1 2 3];
x = randn(3,1);
C = convmtx(b',3);求 b 与 x 的卷积的两种等效方法如下。
y1 = C*x;
y2 = conv(b,x);