题目

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

思路

思路一

该题目可以作为一维前缀和的扩展(参见Leecode-303)。

初始化时对矩阵的每一行计算前缀和，检索时对二维区域中的每一行计算子数组和，然后对每一行的子数组和计算总和。

时间复杂度：初始化 O(mn)，每次检索 O(m)，其中 m 和 n 分别是矩阵 matrix的行数和列数。初始化需要遍历矩阵 matrix计算二维前缀和，时间复杂度是 O(mn)。 每次检索需要对二维区域中的每一行计算子数组和，二维区域的行数不超过 m，计算每一行的子数组和的时间复杂度是 O(1)，因此每次检索的时间复杂度是 O(m)。

空间复杂度：O(mn)，其中 m 和 n 分别是矩阵 matrix的行数和列数。需要创建一个 m行 n+1 列的前缀和数组 sums。

思路二

小学数学，田字形，已知整体面积，上面面积，左边面积，左上面积，求右下角矩形的面积。 右下角矩形的面积=整体面积-上面面积-左边面积+左上面积

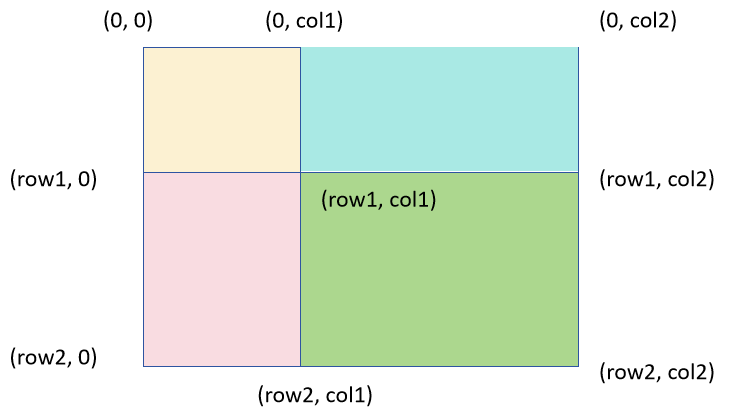
根据上述描述，假设我们计算(row1, col1)，(row2, col2)之间的值，可以使用以下的公式：

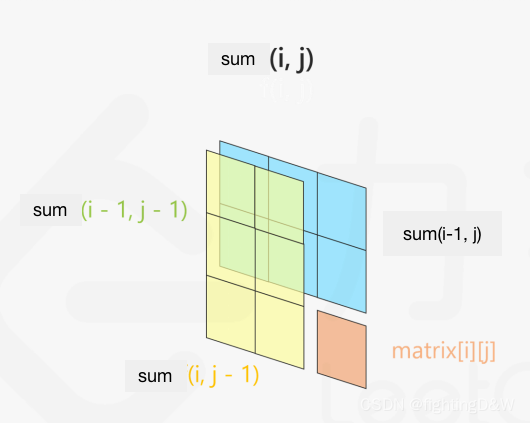
我们在初始化的时候，需要求出上述公式中的。将每个位置的sum[i , j] 对应的放入二位数组的sums[i+1,j+1]。由于此时并不知道sum[i , j]位置中，所有元素的和，因此需要使用拼接的方式进行求解。

时间复杂度：初始化 O(mn)，每次检索 O(1)，其中 m 和 n 分别是矩阵 matrix的行数和列数。 初始化需要遍历矩阵 matrix 计算二维前缀和，时间复杂度是 O(mn)。 每次检索的时间复杂度是 O(1)。

空间复杂度：O(mn)，其中 m 和 n 分别是矩阵 matrix 的行数和列数。需要创建一个 m+1 行 n+1 列的二维前缀和数组 sums。

代码
 

class NumMatrix {int[][] sums;public NumMatrix(int[][] matrix) {int m = matrix.length;if (m > 0) {int n = matrix[0].length;sums = new int[m + 1][n + 1];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];}}}}public int sumRegion(int row1, int col1, int row2, int col2) {return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];}
}