一、并查集
(1)处理问题的类型
1.将两个集合合并
2.询问两个元素是否在一个集合当中
询问
1.fa[x]=a;
2.if(fa[x]==fa[y]) o(1)
在o(1)的复杂度内进行两个操作
(2)基本原理
基本原理:每个集合用一棵树来表示,树根的编号就是整个集合的编号
每个节点存储它的父节点,fa[x]表示x的父节点
1.如何判断树根?
if(fa[x]==x)//判断是树根
2.如何求x的集合编号//复杂度高
while(p[x]!=x)
x=p[x];
优化:把整个路径上的所有点都指向根节点(路径压缩) o(1)
3. 如何合并两个集合
左集合是右边儿子或者右集合是左边儿子
fx是x的集合编号,py是y集合的编号
fa[x]=y;
(3)模板
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=1e5+100;
const int inf=0x3f3f3f3f;
int n,m;
int fa[N];//存的是每个元素的父节点是谁
int find(int x)//返回x的祖宗节点+路径压缩
{if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];
}
void merge(int a,int b)
{fa[find(a)]=find(b);//a的祖宗节点的父亲 =b的祖宗节点
}
void solve()
{cin>>n>>m;int i,j;for(i=1;i<=n;i++){fa[i]=i;}while(m--){char c;int x,y;cin>>c>>x>>y;if(c=='M'){merge(x,y);}else{if(find(x)==find(y))//询问x,y是否在同一个集合中cout<<"Yes"<<endl;elsecout<<"No"<<endl;}}
}
signed main()
{int t=1;while(t--){solve();}return 0;
}
二、相关例题
acwing 837. 连通块中点的数量
一、题目要求
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a和点 b 是否在同一个连通块中,a和 b可能相等;Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a 和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤10^5
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3二、思路
主要解决点a所在连通块中点的数量问题,可以用cnt[N]数组,来记录每个集合中点的数量,设最开始每个集合中点的数量为1,即只有它本身;当需要合并的时候,统计点的数量,假设,a,b两个集合需要合并在一块,将a集合合并在b集合的下面,即a集合的父节点是b,则fa[find(a)]=find(b),则cnt[find(b)]+=cnt[find(a)];

三、代码
/*
统计连通块中点的数量
*/
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=1e5+10;
const int inf=0x3f3f3f3f;
int n,m;
int fa[N];
int cnt[N];//每个集合中点的数量
int find(int x)
{if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];
}
void merge(int a,int b)
{fa[find(a)]=find(b);
}
void solve()
{cin>>n>>m;int i;for(i=1;i<=n;i++){fa[i]=i;cnt[i]=1;//最开始每个集合中只有一个点 }while(m--){string s;int x,y;cin>>s;if(s=="C"){cin>>x>>y; merge(x,y);}else if(s=="Q1"){cin>>x>>y;if(find(x)!=find(y))//只有当x,y不在一个集合里面的时候,才能相加 cnt[find(y)]+=cnt[find(x)];if(find(x)==find(y)) cout<<"Yes"<<endl;elsecout<<"No"<<endl;}else{cin>>x;cout<<cnt[find(x)]<<endl;}}
}
signed main()
{int t=1;while(t--){solve();}return 0;
}
acwing 240. 食物链
一、题目要求
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A 吃 B,B吃 C,C 吃 A。
现有 N个动物,以 1∼N 编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 X或 Y 比 N 大,就是假话;
- 当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
输入格式
第一行是两个整数 N 和 K,以一个空格分隔。
以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1则表示 X和 Y 是同类。
若 D=2,则表示 X 吃 Y。
输出格式
只有一个整数,表示假话的数目。
数据范围
1≤N≤50000
0≤K≤100000
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3二、思路
1.思路
(1).x>n||y>n 假
(2).同类吃同类 假
(3).食物链中的关系?如何记录每个点和根节点的关系?利用数组dis[N];
三种关系,每个点到根节点的距离表示其到根节点的关系
1.一个点到根节点的距离为1 (dis%3==1)吃根节点 1吃0
2.一个点到根节点的距离为2 (dis%3==2)可以被根节点吃 2吃1
3.一个点到根节点的距离为3 (dis%3==0)和根节点为同类 0吃2
根节点就是第0代,所以吃第0代的就是第一代,吃第一代的是第二代,以此类推...
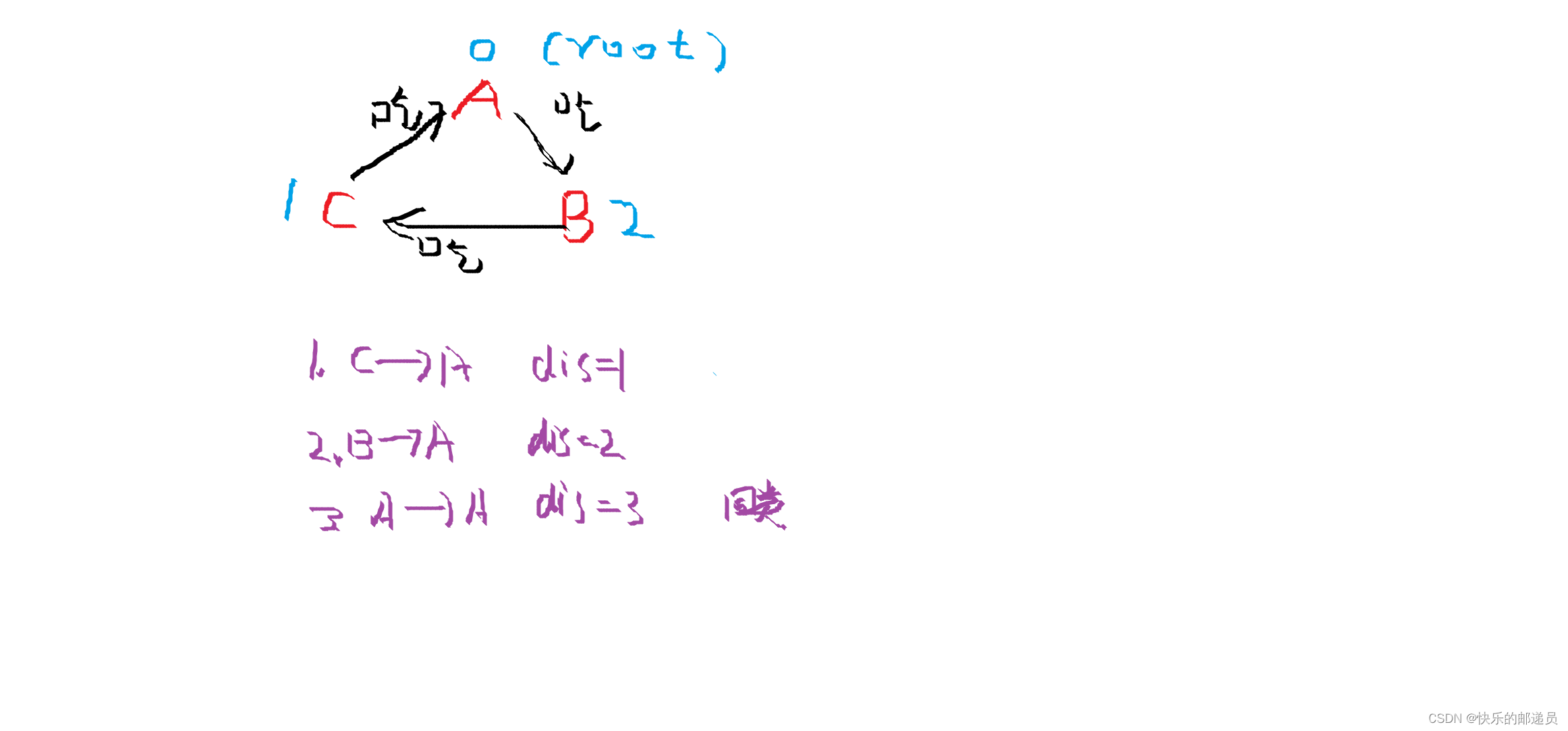
2求dis[N]
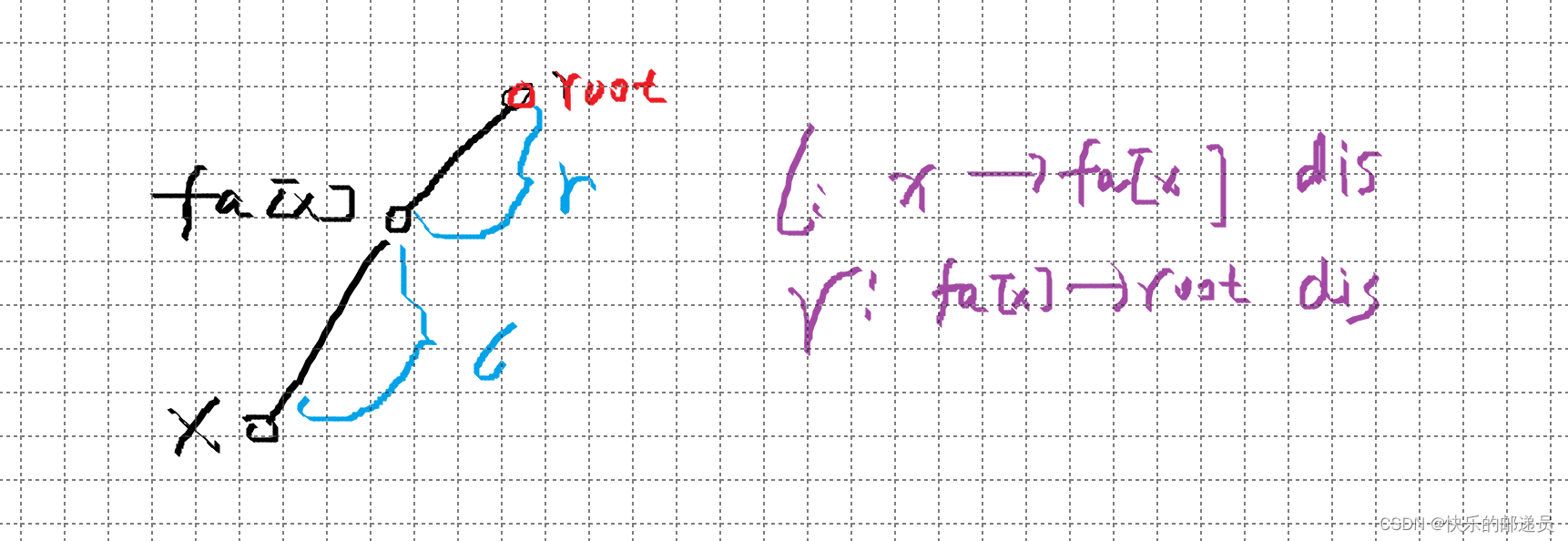
int dis[N]; //记录每个点到根节点的距离
int find(int x)
{if(fa[x]!=x){int u=find(fa[x]);//找到其根节点 dis[x]+=dis[fa[x]];//x到父节点的距离 fa[x]=u;}return fa[x];
}
//初始化(main()函数里面的代码)
cin>>n>>m;
int i,j,k=0;
for(i=1;i<=n;i++)
{fa[i]=i; dis[i]=0;//最开始每个点到根节点的距离为0
}3. (1).x>n||y>n 假
int op,x,y;
cin>>op>>x>>y;
if(x>n||y>n)//超过总数为假cnt++;//记录假语句的个数
(2)1 x,y 代表x y是同类;当op=1,当find(a)==find(b),然而x,y不是同类的时候则为假
让fa[x]指向fa[y],又因为x,y为同类,所以(dis[x]+?)%3=dis[y]%3;
即:(dis[x]+?-dis[y])%3=0;
即:?=dis[y]-dis[x];

int a=find(x),b=find(y);
if(op==1)//在同类中,如果出现不是同类的为假
{if(a==b&&((dis[x]-dis[y])%3!=0))//已经在一个集合中,且不是同类 cnt++;else if(a!=b) //不在一个集合中 ,先将其并到一个集合里面{fa[a]=b; //先将其 变成同类dis[a]=dis[y]-dis[x];//更新代数+距离//(dis[x]+?-dis[y])%3==0 同类//?=dis[y]-dis[x]; }
} (3)如果两者属于同类,有吃与被吃的关系也为假
1.因为x吃y,所以x到根节点的距离比y到根节点的距离多1(在%3d的情况下)
即:(dis[x]-dis[y]-1)%3==0;
2.(dis[x]+?-dis[y]-1)%3=0;
即:?=dis[y]+1-dis[x]
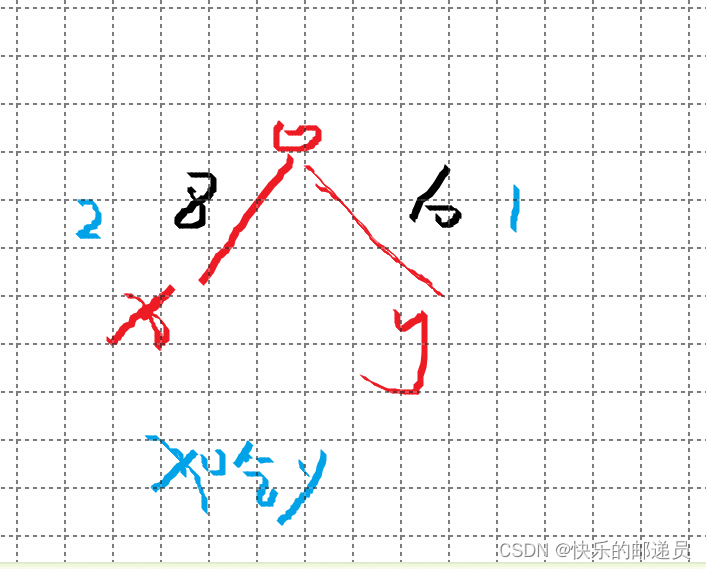
else//在吃与被吃的关系中,如果两者属于同类,有吃与被吃的关系也为假{//dis[x]%3-dis[y]%3=1;说明吃与被吃的关系 //(dis[x]-dis[y]-1)%3==0if(a==b&&((dis[x]-dis[y]-1)%3!=0))//在一个集合中,属于同类,并且x吃y,则也为假cnt++;else if(a!=b)//不是同类,可以吃,更新dis ,更新代数{//(dis[x]+?)%3-(dis[y]%3)-1=0;//dis[x]-dis[y]-1=-?//?=dis[y]+1-dis[x];fa[a]=b;dis[a]=dis[y]+1-dis[x];} }三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int N=1e5+10;
const int inf=0x3f3f3f3f;
int n,m;
int fa[N];
int dis[N]; //记录每个点到根节点的距离
int find(int x)
{if(fa[x]!=x){int u=find(fa[x]);//找到其根节点 dis[x]+=dis[fa[x]];//x到父节点的距离 fa[x]=u;}return fa[x];
}
void solve()
{cin>>n>>m;int i,j,k=0;for(i=1;i<=n;i++){fa[i]=i; dis[i]=0;//最开始每个点到根节点的距离为0 }int cnt=0;while(m--) {int op,x,y;cin>>op>>x>>y;if(x>n||y>n)//超过总数为假cnt++;else {int a=find(x),b=find(y);if(op==1)//在同类中,如果出现不是同类的为假{if(a==b&&((dis[x]-dis[y])%3!=0))//已经在一个集合中,且不是同类 cnt++;else if(a!=b) //不在一个集合中 {fa[a]=b; //先将其 变成同类dis[a]=dis[y]-dis[x];//更新代数+距离//(dis[x]+?-dis[y])%3==0 同类//?=dis[y]-dis[x]; } } else//在吃与被吃的关系中,如果两者属于同类,有吃与被吃的关系也为假{//dis[x]%3-dis[y]%3=1;说明吃与被吃的关系 //(dis[x]-dis[y]-1)%3==0if(a==b&&((dis[x]-dis[y]-1)%3!=0))//在一个集合中,属于同类,并且x吃y,则也为假cnt++;else if(a!=b)//不是同类,可以吃,更新dis ,更新代数{//(dis[x]+?)%3-(dis[y]%3)-1=0;//dis[x]-dis[y]-1=-?//?=dis[y]+1-dis[x];fa[a]=b;dis[a]=dis[y]+1-dis[x];} }}}cout<<cnt<<endl;
}
signed main()
{int t=1;while(t--){solve();}return 0;
}