一，打家劫舍I

题目：

一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响小偷偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组 nums ，请计算 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

题目接口：

class Solution {
public:int rob(vector<int>& nums) {}
};

解题思路及代码：

这个打家劫舍问题便是经典的多状态dp问题。为什么是多状态dp问题呢？

1.首先这道题要我们求得是最大值，并且第i家的最大值其实是由前面的前i-1家推导出来的，所以这个问题可以是一个dp问题。

2.为什么1是个多状态dp问题呢？首先我们知道，我们第i天的最大值是由前面的i-1家推导出来的。但是前面的i-1家里面的每一天其实都有偷与不偷两种状态。所以综上两点我们的这道题目便是一个多状态dp问题了。

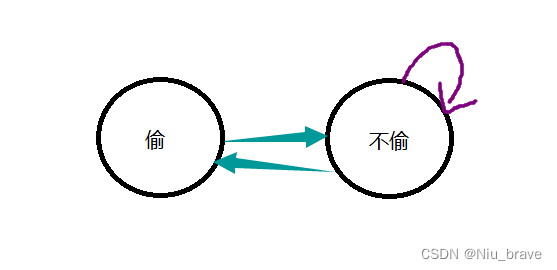
解决这种dp问题的第一步便是画出状态转移的图表示，如下：

首先解释一下箭头，箭头的开始表示的是前一家的状态，箭头的结束表示这一家的状态。

所以要变成这一家不偷的状态便有两种情况：1.上一家偷了，这一家我不偷

                                                                     2.上一家没偷，这一家我还是不偷。

今天变成偷的状态：上一家没偷，这一家偷。（上一家偷了，这一家就不能偷了。题目要求）

有了这一个状态转移关系以后，我们便可以开始我们的题目解答了，代码如下：

class Solution {
public:int rob(vector<int>& nums) {int n = nums.size();//定义两个数组分别代表第i家偷了和没偷的最大值，f表示偷了，g表式没偷vector<int>f(n);auto g = f;//初始化f[0] = nums[0];//第一家偷了g[0] = 0;//第一家没偷//根据状态转移图填表for(int i = 1;i<n;i++){f[i] = g[i-1]+nums[i];//上一家没偷，这一家才能偷g[i] = max(g[i-1],f[i-1]);//不管上一家偷不偷，这一家都不偷，取前面一家在两种状态下的最大值。}return max(g[n-1],f[n-1]);//返回每一家都到访后的最大值}
};