最小生成树算法
Prime算法
算法思路:从已选顶点所关联的未选边中找出权重最小的边,并且生成树不存在环。
其中,已选顶点是构成最小生成树的结点,未选边是不属于生成树中的边。
例子:

第一步:
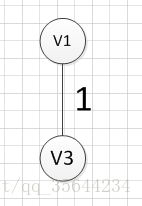
假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1:
第二步:

在v1,v3相关联的边中选一个权值最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—-v6=4

然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—-v4=2.

然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5

然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3

最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
Kruskal算法
算法思路:
(1)将边按权值从小到大的顺序添加到新图中,保证添加的过程中不会形成环(2)重复上一步直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
(3) n个顶点,n-1条边
例子 :
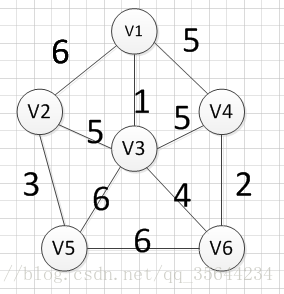
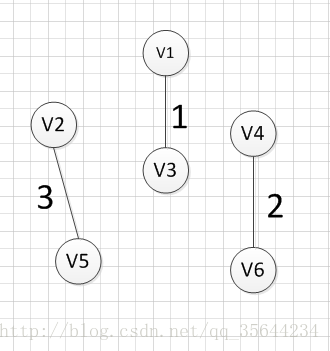
首先完整的图如下图:
然后,我们需要从这些边中找出权重最小的那条边,可以发现边(v1,v3)这条边的权重是最小的,所以我们输出边:v1—-v3=1
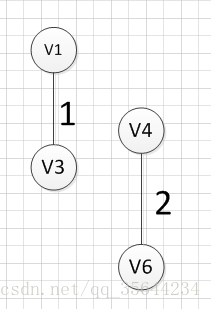
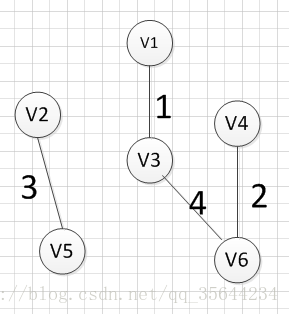
然后,我们需要在剩余的边中,再次寻找一条权重最小的边,可以发现边(v4,v6)这条边的权重最小,所以输出边:v4—v6=2
然后,我们再次从剩余边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以可以输出边:v2—-v5=3,
然后,我们使用同样的方式找出了权重最小的边:(v3,v6),所以我们输出边:v3—-v6=4
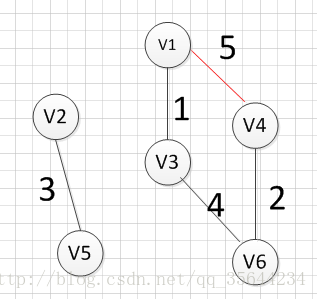
好了,现在我们还需要找出最后一条边就可以构造出一颗最小生成树,但是这个时候我们有三个选择:(v1,V4),(v2,v3),(v3,v4),这三条边的权重都是5,首先我们如果选(v1,v4)的话,得到的图如下:
我们发现,这肯定是不符合我们算法要求的,因为它出现了一个环,所以我们再使用第二个(v2,v3)试试,得到图形如下:
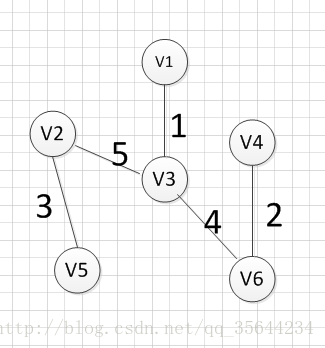
我们发现,这个图中没有环出现,而且把所有的顶点都加入到了这颗树上了,所以(v2,v3)就是我们所需要的边,所以最后一个输出的边就是:v2—-v3=5
拓扑排序
首先建立(n个顶点的)AOV网
(1) 在AOV网络中选一个没有直接前驱的顶点(入度为0的顶点),并输出之;
(2)从途中删去该顶点,同时删去所有它发出的边;
重复(1)和(2),直到全部顶点均已输出,拓扑有序序列形成,拓扑排序完成;
若图中还有未输出的顶点,但已跳出处理循环,这说明图中存在环;
AOV网络(Activity On VertexNetwork)
不能出现有向回路,即有向环。在AOV网络中如果出现了有向环,则意味着某项活动应以自己作为先决条件。
关键路径

最早最晚时间:
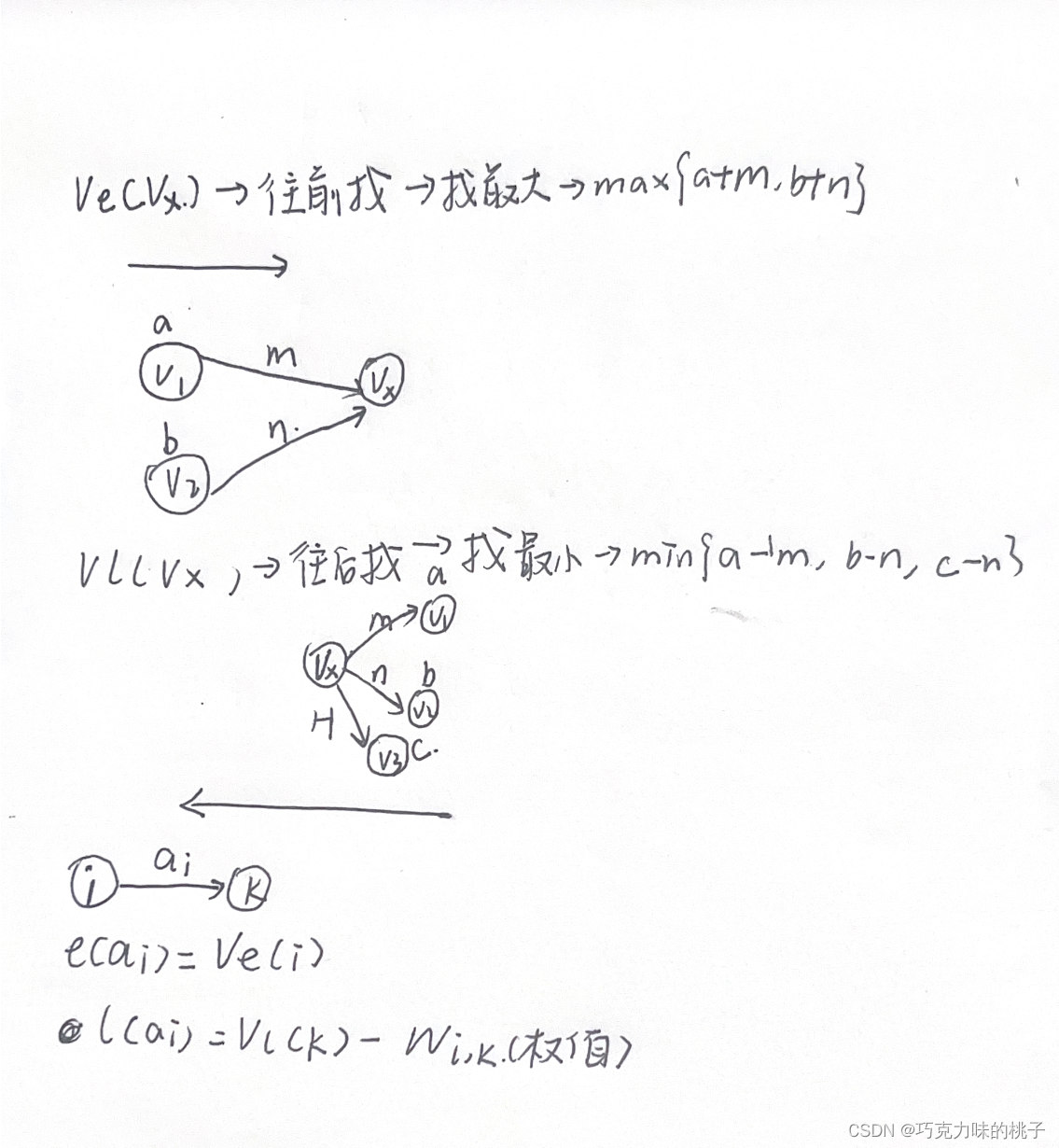
(1)事件vk的最早发生时间ve(k):决定了所有从vk开始的活动能够开工的最早时间;
(2)活动ai的最早开始时间e(i):指该活动弧的起点所表示的事件的最早发生时间;
(3)事件vk的最迟发生时间vl(k):指在不推迟整个工程完成的前提下,该事件最迟必须发生的时间;
若一个活动的时间余量为0,则说明该活动必须要如期完成,d(i)=0即l(i)=e(i)的活动ai是关键活动,由关键活动组成的路径就是关键路径。
步骤:
(1)求所有事件的最早发生时间ve();(2)求所有事件的最迟发生时间vl();
(3)求所有活动的最早发生事件e();
(4)求所有活动的最迟发生时间l();
(5)求所有活动的时间余量d();
(6)d(i)=0的就是关键活动,所有关键活动组成的路径即为关键路径。
ve(源点)等于0,vl(源点)需要自己算
ve(汇点)=vl(汇点) 需要自己算