参加了此次比赛,收获很多,两个半小时让我体会到了很多,所以想做个总结
第十五届全国大学生数学竞赛初赛试题
(非数学A类,2023年)

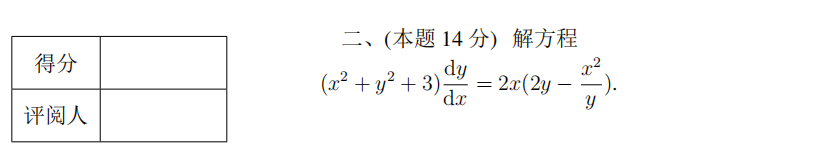

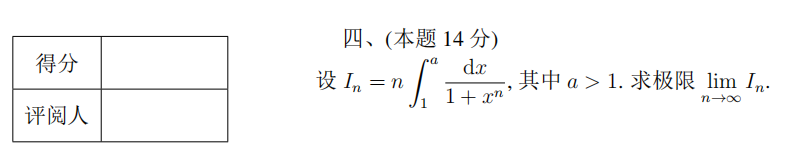


下面是答案解析,有兴趣的小伙伴可以做完对照一下。
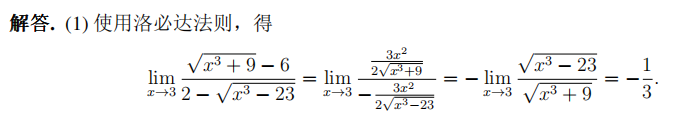
直接使用洛必达一次即可求出结果,但是要注意符号,很多人粗心忘掉分母求导后的负号。

常规考点,要注意y*f2对y求导数时存在,不要漏项。

主要是考察高阶求导的公式,在同济版高数教材的98页给出了此公式的应用示例如下:
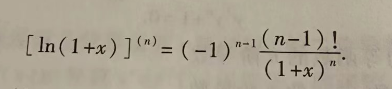

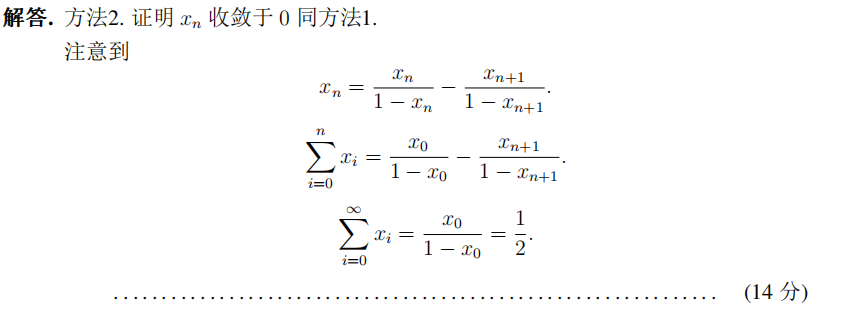
此题考查级数,要注意端点是否符合,不要根据做题经验一概而论,要细心验证。
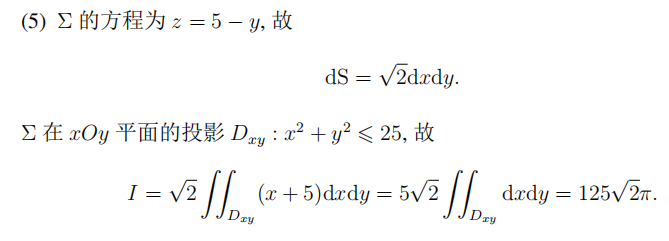

这题微分方程有点子颠覆了我的认知,我才疏学浅,看到的时候真的很懵,当时试了好多方法都没算出来。


我感觉这道题比较新颖,我还是第一次遇到圆锥体卡椭球的
参考解析画图。立体就是一个平面去截取一个旋转椭球面得到一个截面圆,以该圆为准线的圆锥面与位于该圆右侧的椭球面它们围成的立体,所以直接就用圆锥体体积减去截取部分的旋转椭球面的体积就行。也就是yOz面上的直线、曲线段与y轴围成的区域绕y轴旋转所得立体的体积,这就是最为典型,也是非常简单的立体体积计算问题,旋转体体积的计算,利用定积分可以直接计算得到。即
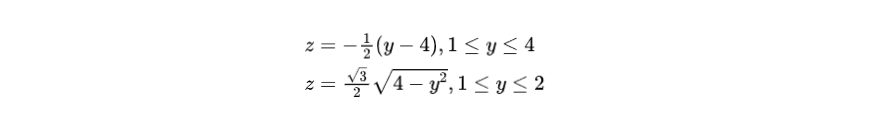
两个定积分的计算都非常简单、容易计算!
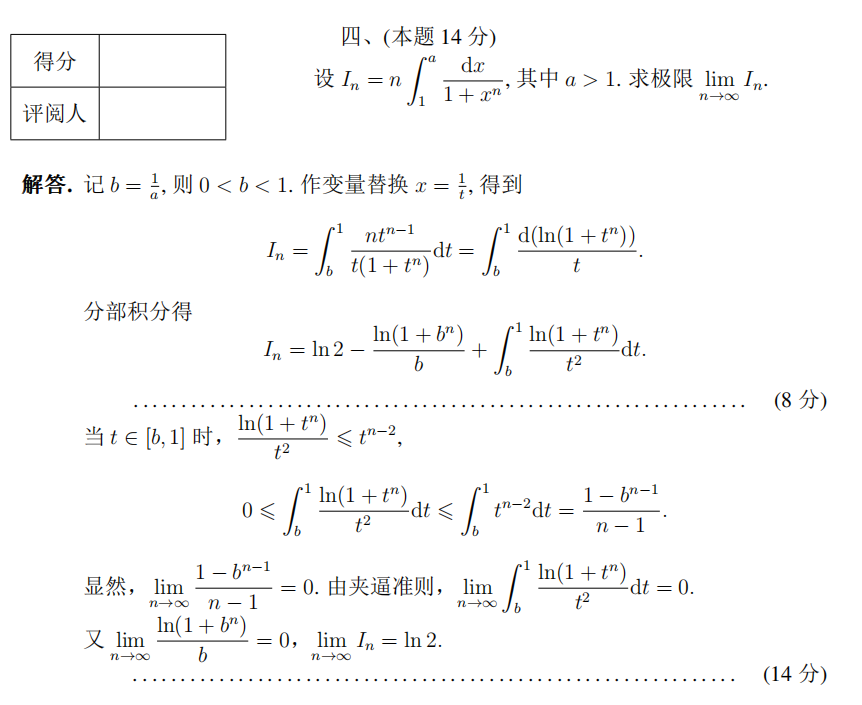
参考解析对于这个题目,从两个方面来考察转换为咱们熟悉的问题。第一,倒代换将分母的高次向分子转移;第二,定积分求极限问题转换为熟悉的积分范围[0,1]内的区间方便放缩。对于能够计算的定积分尽可能计算化简转换成为方便放缩的表达式。所以逐步可能得到需要的解题过程,对于参考解答分部积分得到表达式
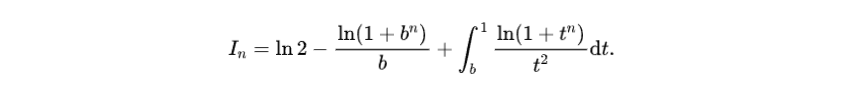
由于0<b<1,第二项直接得到极限为0,第二项积分项基于积分中值定理也可以直接得到积分值趋于0。从而轻松得到极限结果。


参考解析中积分不等式证明的辅助函数的构造,积分不等式证明中柯西积分不等式的应用,一般可以凑出可能的证明思路。这也属于抽象的,包含函数乘积的定积分不等式证明的比较经典的一类题型,相对有比较固定的探索可能的验证方法的思路。