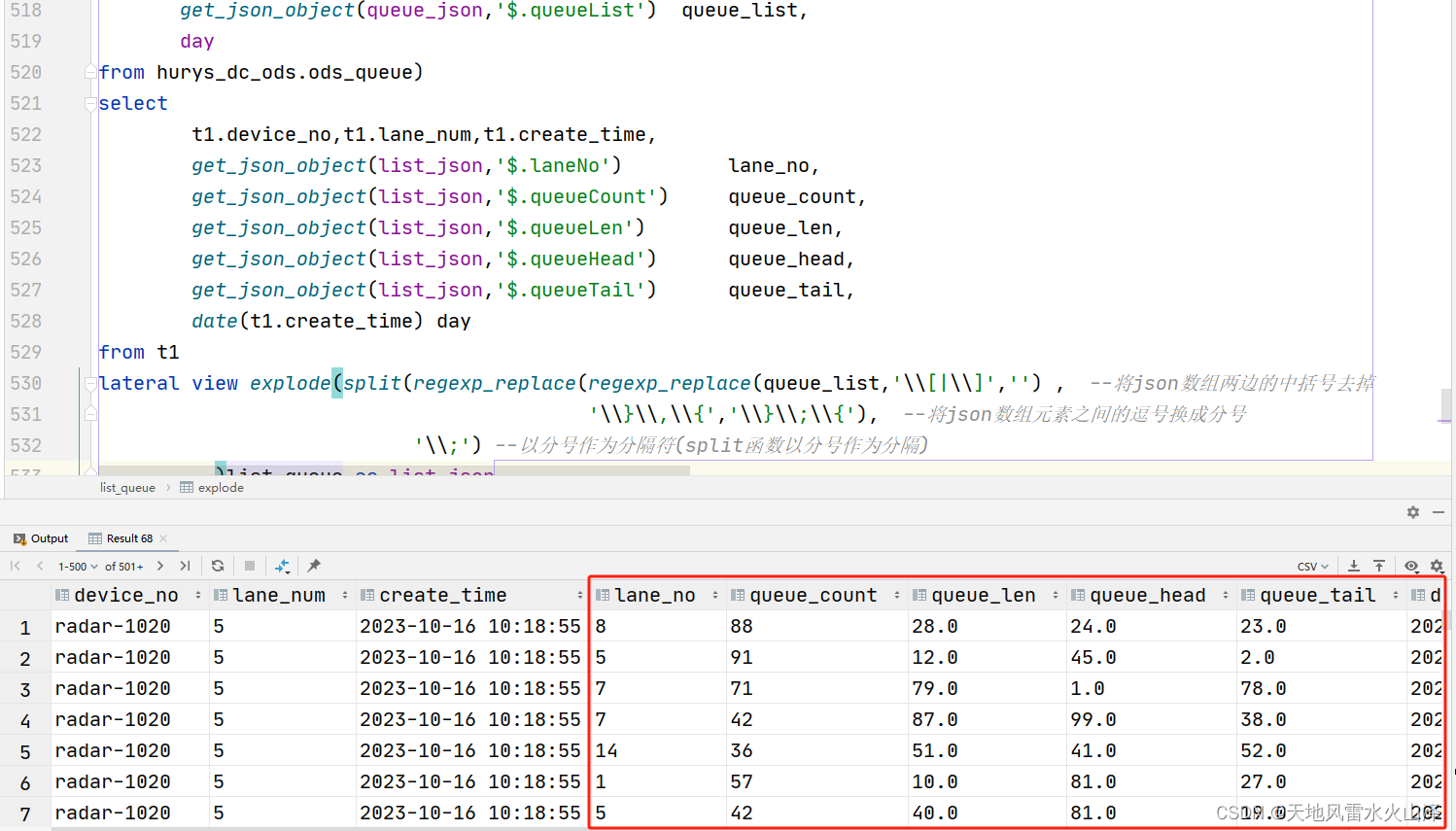
1 有监督学习的损失函数
1.1 分类问题
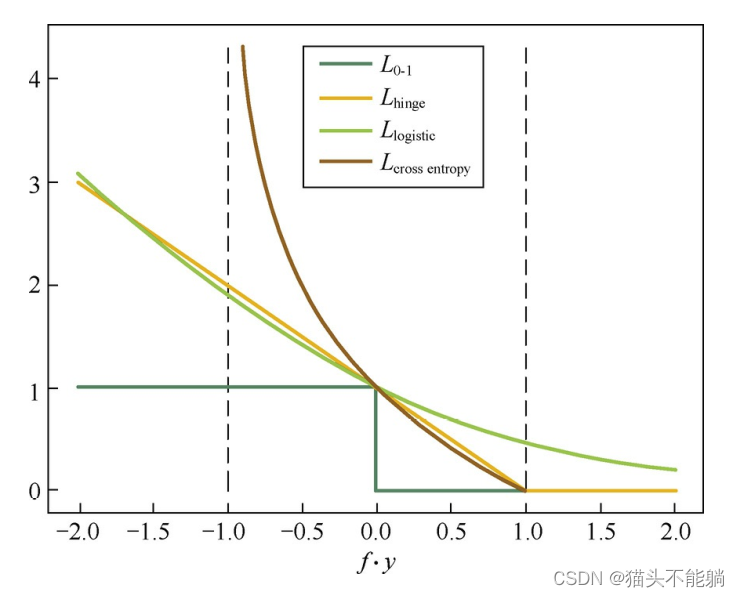
对二分类问题, Y={1,−1}, 我们希望sign f(xi,θ)=yi, 最自然的损失函数是0-1损失,
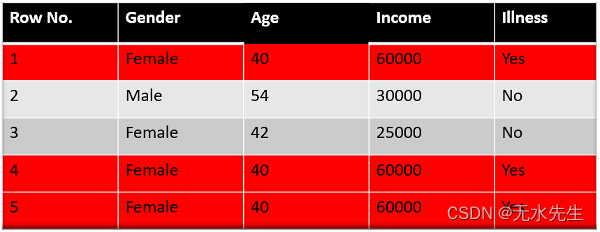
| 函数定义 | 特点 | |
|---|---|---|
| 0-1损失函数 | 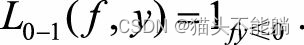 | 非凸、非光滑,很难直接对该函数进行优化 |
| Hinge损失函数 | 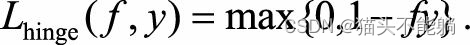 | 当fy≥1时, 该函数不对其做任何惩罚。 Hinge损失在fy=1处不可导, 因此不能用梯度下降法进行优化, 而是用次梯度下降法 |
| Logistic损失函数 |  | 该损失函数对所有的样本点都有所惩罚, 因此对异常值相对更敏感一些 |
| 交叉熵损失函数 | 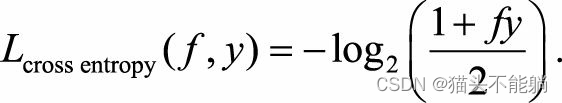 |
1.2回归问题
希望 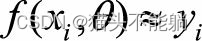 , 最常用的损失函数是平方损失函数
, 最常用的损失函数是平方损失函数
| 函数定义 | 特点 | |
|---|---|---|
| 平方损失函数 | 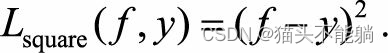 | 对异常点比较敏感 |
| 绝对损失函数 | 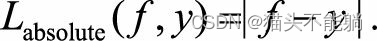 | 在f=y处无法求导数 |
| Huber损失函数 |  | 在 |

2 梯度下降法
梯度下降算法发展过程
3 L1正则化与稀疏性
稀疏性,就是模型中的很多参数为0,相当于对模型进行了特征选择,只留下了重要的特征。提高了模型的泛化能力,降低了过拟合的可能。
为什么L1正则化能让模型具有稀疏性?
3.1 从解空间形状来看

黄色的部分是L2和L1正则项约束后的解空间, 绿色的等高线是凸优化问题中目标函数的等高线,L2正则项约束后的解空间是圆形, 而L1正则项约束的解空间是多边形。显然, 多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。
3.2 从函数叠加来看
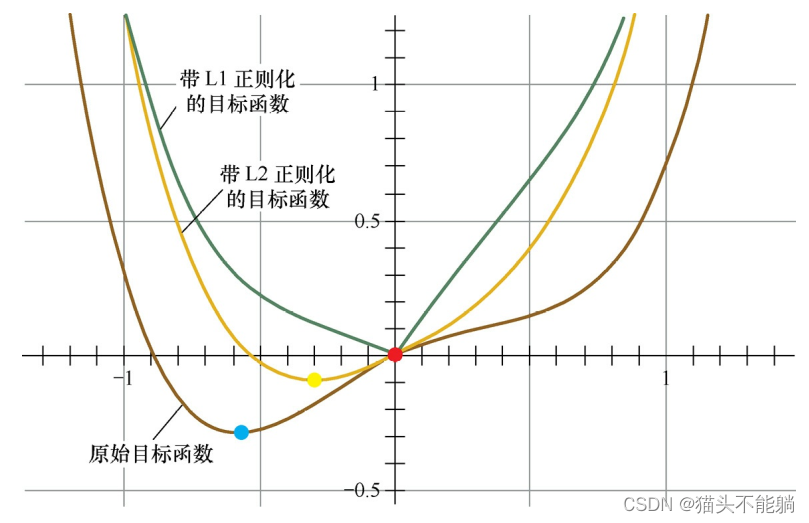
首先, 考虑加上L2正则化项, 目标函数变成L(w)+Cw2, 其函数曲线为黄色。此时, 最小值点在黄点处, 对应的w*的绝对值减小了, 但仍然非0。
然后, 考虑加上L1正则化项, 目标函数变成L(w)+C|w|, 其函数曲线为绿色。此时, 最小值点在红点处, 对应的w是0, 产生了稀疏性。
在一些在线梯度下降算法中, 往往会采用截断梯度法来产生稀疏性, 这同L1正则项产生稀疏性的原理是类似的。
3.3从贝叶斯实验来看
从贝叶斯的角度来理解L1正则化和L2正则化, 简单的解释是, L1正则化相当于对模型参数w引入了拉普拉斯先验, L2正则化相当于引入了高斯先验, 而拉普拉斯先验使参数为0的可能性更大。