LBFGS

pytorch的LBFGS也是一个优化器
但是与一般的优化器不同
平常我们的顺序是

loss=criterion(predict, gt)
optim.zero_grad()
loss.backward()
optim.step()

而LBFGS是

def closure():optim.zero_grad()loss = criterion(predict, gt)loss.backward()return lossoptim.step(closure)

例子

考虑
$$f\left(x,y\right)={\left(1-x\right)}^2+100{\left(y-x^2\right)}^2$$
这是一个非凸的函数，$f\left(x,y\right)\ge f\left(1,1\right)=0$

#!/usr/bin/env python
# _*_ coding:utf-8 _*_
import torch
from torch import optim
import matplotlib.pyplot as plt# 2d Rosenbrock function
def f(x):return (1 - x[0]) ** 2 + 100 * (x[1] - x[0] ** 2) ** 2# Gradient descent
x_gd = 10 * torch.ones(2, 1)
x_gd.requires_grad = True
gd = optim.SGD([x_gd], lr=1e-5)
history_gd = []
for i in range(100):gd.zero_grad()objective = f(x_gd)objective.backward()gd.step()history_gd.append(objective.item())# L-BFGS
def closure():lbfgs.zero_grad()objective = f(x_lbfgs)objective.backward()return objectivex_lbfgs = 10 * torch.ones(2, 1)
x_lbfgs.requires_grad = Truelbfgs = optim.LBFGS([x_lbfgs],history_size=10,max_iter=4,line_search_fn="strong_wolfe")history_lbfgs = []
for i in range(100):history_lbfgs.append(f(x_lbfgs).item())lbfgs.step(closure)# Plotting
plt.semilogy(history_gd, label='GD')
plt.semilogy(history_lbfgs, label='L-BFGS')
plt.legend()
plt.show()

运行结果

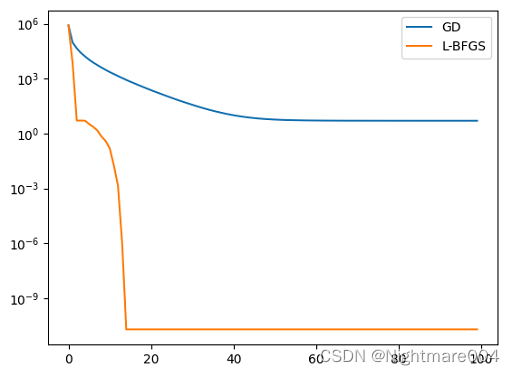
图是当前的函数值
可以看出L-BFGS的结果更好