BST定义
BST - Binary Search Tree, 即二叉搜索树(有序二叉树)
特性
- 中序遍历有序
- 查找/插入/删除某个数值可以通过
即树的高度,最优
,最坏
.
- 有多种改进BST可以动态维持插入删除后树结构能尽可能保持平衡

BST基本操作
查询 - 二分查找
- 搜索数值 - 二分法
class Solution {public TreeNode searchBST(TreeNode root, int val) {while(root!=null) {if (root.val<val) {root = root.right;} else if (root.val>val) {root = root.left;} else {return root;}}return null; }
}- 搜索临近数值
class Solution {double min = Double.MAX_VALUE;int res = -1;public int closestValue(TreeNode root, double target) {dfs(root, target);return res;}private void dfs(TreeNode root, double target) {if (root==null) return;if (Math.abs(root.val - target) < min) {min = Math.abs(root.val - target);res = root.val;} else if (Math.abs(root.val - target) == min) {res = root.val<res? root.val: res;}if (root.val>target) dfs(root.left, target);else dfs(root.right, target);}
}插入
插入则是首先找到需要插入的位置,然后插入新结点
class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {return dfs(root, val);}private TreeNode dfs(TreeNode root, int val) {if (root==null) {root = new TreeNode(val);return root;}if (root.val > val) root.left = dfs(root.left, val);else root.right = dfs(root.right, val);return root; }
}删除
删除操作较为复杂一点,我们在删除之后还需要维护当前二叉搜索树的性质,有三种情况:
- 删除叶子结点,不会影响BST性质,直接删除即可
- 删除结点没有右子树,也就是删除后左子树不会影响BST性质,将左子树root直接顶替删除结点的位置即可
- 删除结点有左右子树,为了保证BST性质,我们选择删除点的后继结点作为顶替结点,也就是删除结点右子树最左边的那个点,因为可以保证右子树所有点都大于该点,维持了BST性质
class Solution {public TreeNode deleteNode(TreeNode root, int key) {/**删除三种情况1. 叶子结点2. 只存在一个子树3. 左右都存在子树*/return dfs(root, key);}private TreeNode dfs(TreeNode root, int key) {if (root==null) return null;if (root.val==key) {if (root.left==null && root.right==null) return null;else if (root.left==null || root.right==null) {if (root.left!=null) return root.left;if (root.right!=null) return root.right;} else {// 找到root的后继结点,也就是右子树最左边的那个点TreeNode dum = root.right;while (dum.left!=null) {dum = dum.left;}root.val = dum.val;root.right = dfs(root.right, root.val);}} else if (root.val>key) {root.left = dfs(root.left, key);} else {root.right = dfs(root.right, key);}return root;}
}前驱/后继结点
Leetcode 285
求解某一个点的前驱结点思路存储一个变量prev来保存进行下一层递归前的结点信息,如果中序遍历递归遍历到目标结点,其实保存的prev就是该结点的前驱结点
private void preSuccessor(TreeNode root, TreeNode p) {if (node==null) return;preSuccessor(node.left, p);if (root==p) return prev;prev = root;preSuccessor(node.right, p);
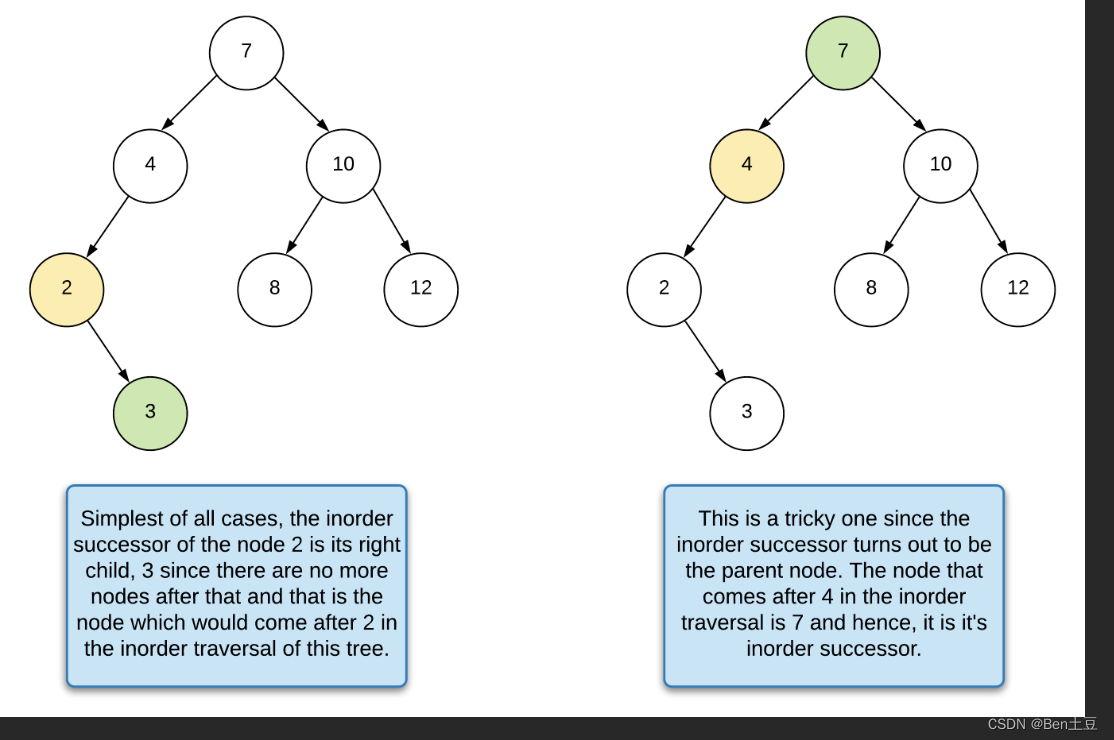
}求解后躯结点较为复杂,需要考虑到几种情况:
- 目标结点有右子树,那么后继结点则是右子树中leftmost结点
- 如果目标结点没有右子树,那么后继结点则可能是parent中的某个结点
求解上述第二类后继结点思路类似,前驱结点是当前递归层处理的结点是目标结点时,prev保存的值即为前驱结点;后继结点可以理解为当前递归层的前驱结点时目标结点时,那么当前结点就是目标结点的后继结点,有点逆向思维哈哈。

class Solution {// 需要前驱结点信息TreeNode prev;TreeNode insuccessor;public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {if (p.right!=null) {TreeNode node = p.right;while (node.left!=null) {node = node.left;}return node;} else {helper(root, p);}return insuccessor;}private void helper(TreeNode node, TreeNode p) {if (node==null) return;helper(node.left, p);// check 当前结点if (prev!=null && prev==p) {insuccessor = node;}prev = node; //如果 当前结点前驱结点==p那么这个结点就是p的后驱结点helper(node.right, p);}
}验证是否为BST
Leetcode 98. Validate BST
基本思路就是确保左结点 < 根结点 < 右结点,但是还需要保证局部正确的同时,左子树全部结点 < 根结点 < 右子树全部结点。所以每一次向下递归左子树时要以当前结点值作为上限值,遍历右子树时以当前结点值作为下限值
class Solution {public boolean isValidBST(TreeNode root) {return helper(root, null, null);}private boolean helper(TreeNode root, Integer low, Integer high) {if (root==null) return true;if ((low!=null && root.val<=low) || (high!=null && root.val>=high)) {return false;}return helper(root.left, low, root.val) && helper(root.right, root.val, high);}
}