文章目录
- 题目描述与示例
- 题目描述
- 输入描述
- 输出描述
- 示例
- 输入
- 输出
- 说明
- 解题思路
- 如何表示一个子矩阵
- 暴力解法
- 二维前缀和优化
- 二维前缀和矩阵的构建
- 代码
- 解法一:二维前缀和
- Python
- Java
- C++
- 时空复杂度
- 解法二:暴力解法(不推荐)
- Python
- Java
- C++
- 时空复杂度
- 华为OD算法/大厂面试高频题算法练习冲刺训练
题目描述与示例
题目描述
给定一个二维整数矩阵,要在这个矩阵中。选出一个子矩阵,使得这个子矩阵内所有的数字和尽量大
我们把这个子矩阵称为 “和最大子矩阵”,子矩阵的选取原则,是原矩阵中一段相互连续的矩形区域
输入描述
输入的第一行包含两个整数N,M
(1 <= N, M <= 10)
表示一个 N 行 M 列的矩阵
下面有N行 每行有M个整数
同一行中每两个数字之间有一个空格
最后一个数字后面没有空格
所有的数字得在-1000 ~ 1000之间
输出描述
输出一行,一个数字。表示选出的“和最大子矩阵”内所有数字的和
示例
输入
3 4
-3 5 -1 52 4 -2 4
-1 3 -1 3
输出
20
说明
一个3*4的矩阵中 后面3列的和为20,和最大
解题思路
如何表示一个子矩阵
一个子矩阵可以由四个参数决定,分别为上底、下底、左宽、右宽,分别用变量a、b、c、d表示的话,如下图中灰色区域为通过四个参数所确定的矩形。

如果我们想要枚举所有子矩阵,只需要分别枚举a、b、c、d,写一个4层嵌套的for循环即可。
for a in range(n):for b in range(a, n):for c in range(m):for d in range(c, m):pass
暴力解法
暴力解法是很容易想到的,我们只需要枚举所有的子矩阵,然后对每一个子矩阵进行矩阵内所有元素求和即可。其核心代码为
for a in range(n):for b in range(a, n):for c in range(m):for d in range(c, m):submat_sum = 0for i in range(a, b+1):for j in range(c, d+1):submat_sum += mat[i][j]ans = max(submat_sum, ans)
注意到会出现6层for循环嵌套,时间复杂度为 O ( n 3 m 3 ) O(n^3m^3) O(n3m3)。由于数据范围为(1 <= n, m <= 10),故取最大值时复杂度约为 O ( 1 0 6 ) O(10^6) O(106),无法通过全部用例,故应该思考如何优化。
二维前缀和优化
注意,该方法和LeetCode 304、二维区域和检索 - 矩阵不可变 是类似的。
注意到每一个子矩阵的计算都可以用以下方式进行拆解。
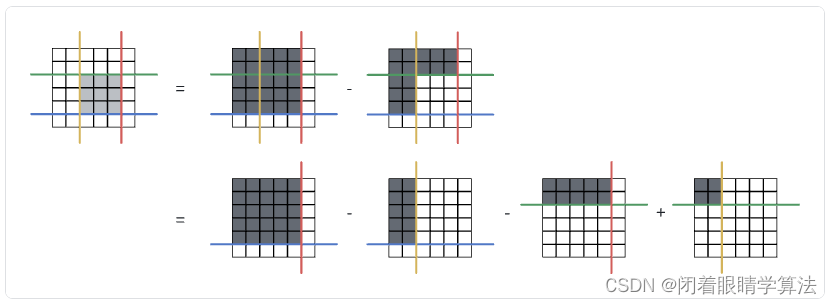
拆解后的四个区域具有一个共同的特点:它们的上底均为上边界、左宽均为左边界。
因此需要考虑类似一维前缀和的方法,将所有的上底为上边界、左宽为左边界(即a = 0,c = 0)的子矩阵的和提前记录在二维前缀和矩阵pre_sum_mat中。
pre_sum_mat是一个大小为(n+1)*(m+1)的矩阵,pre_sum_mat[i][j]表示以第0行、第0列为开头(取得到的开区间),第i行、第j列为结尾(取不到的闭区间)的子矩阵的和。
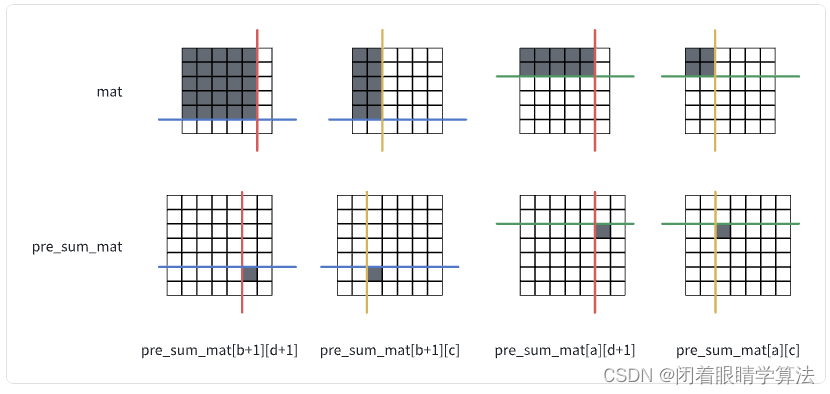
上述的四个区域的和,就可以分别使用pre_sum_mat[b+1][d+1],pre_sum_mat[b+1][c],pre_sum_mat[a][d+1],pre_sum_mat[a][c]来表示了。
这里对开/闭区间的理解是非常重要的,如果想不清楚的话,后面的代码很容易出错。如果把子矩阵用一种类似切片的方法表示(并不严谨的写法)为mat[a:b+1][c:d+1]。那么上述的分析过程可以写为
sum(mat[a:b+1][c:d+1])
= sum(mat[:b+1][:d+1]) + sum(mat[:a][:c]) - sum(mat[:b+1][:c]) - sum(mat[:a][:d+1])
= pre_sum_mat[b+1][d+1] + pre_sum_mat[a][c] - pre_sum_mat[b+1][c] - pre_sum_mat[a][d+1]
那么,在原矩阵mat中,分别以a、b、c、d为上底、下底、左宽、右宽的子矩阵的和,就可以记为
submat_sum = (pre_sum_mat[b+1][d+1] + pre_sum_mat[a][c] -pre_sum_mat[b+1][c] - pre_sum_mat[a][d+1])
上述计算的时间复杂度为O(1),因此这种做法规避了暴力解对子矩阵求和时出现的反复计算,降低了最内层求和时时间复杂度。如果把外部的循环体加上,代码为
for a in range(n):for b in range(a, n):for c in range(m):for d in range(c, m):submat_sum = pre_sum_mat[b+1][d+1] + pre_sum_mat[a][c] - \pre_sum_mat[b+1][c] - pre_sum_mat[a][d+1]ans = max(submat_sum, ans)
如果不想让最内层的索引出现+1,则可以修改for循环的范围,代码变为
for a in range(n):for b in range(a+1, n+1):for c in range(m):for d in range(c+1, m+1):submat_sum = pre_sum_mat[b][d] + pre_sum_mat[a][c] - \pre_sum_mat[b][c] - pre_sum_mat[a][d]ans = max(submat_sum, ans)
上述过程的时间复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2)。当n、m取最大值时复杂度约为 O ( 1 0 4 ) O(10^4) O(104),可以通过全部用例。
二维前缀和矩阵的构建
二维前缀和矩阵pre_sum_mat的构建也要用到类似上述的拆分过程,其核心代码如下
pre_sum_mat = [[0] * (m+1) for _ in range(n+1)]
for i in range(1, n+1):for j in range(1, m+1):pre_sum_mat[i][j] = pre_sum_mat[i-1][j] + pre_sum_mat[i][j-1] - \pre_sum_mat[i-1][j-1] + mat[i-1][j-1]
要特别注意二维前缀和pre_sum_mat的大小,在两个维度上均比原矩阵矩阵mat大1。
该过程的时间复杂度为 O ( n m ) O(nm) O(nm)。
代码
解法一:二维前缀和
Python
# 题目:2023B-最大子矩阵和
# 分值:200
# 作者:闭着眼睛学数理化
# 算法:二维前缀和
# 代码有看不懂的地方请直接在群上提问from math import infn, m = map(int, input().split())
mat = list()
for _ in range(n):row = list(map(int, input().split()))mat.append(row)# 构建二维前缀和数组
pre_sum_mat = [[0] * (m+1) for _ in range(n+1)]
for i in range(1, n+1):for j in range(1, m+1):pre_sum_mat[i][j] = pre_sum_mat[i-1][j] + pre_sum_mat[i][j-1] - \pre_sum_mat[i-1][j-1] + mat[i-1][j-1]# 初始化答案为负无穷小
ans = -inf# 枚举上底a
for a in range(n):# 枚举下底bfor b in range(a, n):# 枚举左宽cfor c in range(m):# 枚举右宽dfor d in range(c, m):# 此时四个参数能够表示一个子矩阵# 根据式子计算子矩阵和,更新anssubmat_sum = pre_sum_mat[b+1][d+1] + pre_sum_mat[a][c] - \pre_sum_mat[b+1][c] - pre_sum_mat[a][d+1]ans = max(submat_sum, ans)print(ans)
Java
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int[][] mat = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {mat[i][j] = scanner.nextInt();}}int[][] preSumMat = new int[n + 1][m + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {preSumMat[i][j] = preSumMat[i - 1][j] + preSumMat[i][j - 1] - preSumMat[i - 1][j - 1] + mat[i - 1][j - 1];}}int ans = Integer.MIN_VALUE;for (int a = 0; a < n; a++) {for (int b = a; b < n; b++) {for (int c = 0; c < m; c++) {for (int d = c; d < m; d++) {int submatSum = preSumMat[b + 1][d + 1] + preSumMat[a][c] - preSumMat[b + 1][c] - preSumMat[a][d + 1];ans = Math.max(submatSum, ans);}}}}System.out.println(ans);}
}
C++
#include <iostream>
#include <vector>
#include <limits>using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> mat(n, vector<int>(m));for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> mat[i][j];}}vector<vector<int>> pre_sum_mat(n + 1, vector<int>(m + 1, 0));for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {pre_sum_mat[i][j] = pre_sum_mat[i - 1][j] + pre_sum_mat[i][j - 1] - pre_sum_mat[i - 1][j - 1] + mat[i - 1][j - 1];}}int ans = numeric_limits<int>::min();for (int a = 0; a < n; a++) {for (int b = a; b < n; b++) {for (int c = 0; c < m; c++) {for (int d = c; d < m; d++) {int submat_sum = pre_sum_mat[b + 1][d + 1] + pre_sum_mat[a][c] - pre_sum_mat[b + 1][c] - pre_sum_mat[a][d + 1];ans = max(submat_sum, ans);}}}}cout << ans << endl;return 0;
}
时空复杂度
时间复杂度: O ( n 2 m 2 ) O(n^2m^2) O(n2m2)。
空间复杂度: O ( n m ) O(nm) O(nm)。二维前缀和矩阵所占空间。
解法二:暴力解法(不推荐)
Python
# 题目:2023B-最大子矩阵和
# 分值:200
# 作者:闭着眼睛学数理化
# 算法:暴力解
# 代码有看不懂的地方请直接在群上提问from math import infn, m = map(int, input().split())
mat = list()
for _ in range(n):row = list(map(int, input().split()))mat.append(row)# 初始化答案为负无穷小
ans = -inffor a in range(n):for b in range(a, n):for c in range(m):for d in range(c, m):submat_sum = 0for i in range(a, b+1):for j in range(c, d+1):submat_sum += mat[i][j]ans = max(submat_sum, ans)print(ans)
Java
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int[][] mat = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {mat[i][j] = scanner.nextInt();}}int ans = Integer.MIN_VALUE;for (int a = 0; a < n; a++) {for (int b = a; b < n; b++) {for (int c = 0; c < m; c++) {for (int d = c; d < m; d++) {int submatSum = 0;for (int i = a; i <= b; i++) {for (int j = c; j <= d; j++) {submatSum += mat[i][j];}}ans = Math.max(submatSum, ans);}}}}System.out.println(ans);}
}
C++
#include <iostream>
#include <vector>
#include <climits>using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> mat(n, vector<int>(m));for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {cin >> mat[i][j];}}int ans = INT_MIN;for (int a = 0; a < n; a++) {for (int b = a; b < n; b++) {for (int c = 0; c < m; c++) {for (int d = c; d < m; d++) {int submatSum = 0;for (int i = a; i <= b; i++) {for (int j = c; j <= d; j++) {submatSum += mat[i][j];}}ans = max(submatSum, ans);}}}}cout << ans << endl;return 0;
}
时空复杂度
时间复杂度: O ( n 3 m 3 ) O(n^3m^3) O(n3m3)。
空间复杂度: O ( 1 ) O(1) O(1)。
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务100+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 大厂真题汇总 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多