机器学习多步时间序列预测解决方案

近年来，随着机器学习与深度学习的发展机器学习平台的成熟，数据科学家们不再需要关心底层的基础设施及构建复杂的训练与推理环境，从而可以把主要的时间与精力放在数据与算法本身。在机器学习变得更容易的今天，越来越多的传统行业已经开始使用机器学习算法来解决现实中的问题，降低成本及提升效率。在能源、制造及零售快消等传统行业中，多步回归预测任务是较为常见的业务场景之一。

例如：您是一家超市的经理，想要预测未来几周的销售情况，并且已经获得了数百种产品的每日销售历史数据。您将面临的问题是什么样的？

时间序列预测（如 ARIMA, Exponential Smoothing 等）可能会很自然地出现在您的脑海中。使用此类算法，您可以将产品的销量作为单独的时间序列，并根据其历史销量来推算其未来的销售额。

然而，您可能会发现每个产品的销售并非独立的，它们之间或许存在着某种依赖性。例如，在夏天时，空调的销量会增加，同时羽绒服的销量会下降。当存在着多个变量时，我们就需要使用多变量时间序列预测(multi-variable time series forecasting)来处理变量间的相关性。

此外，您希望的是预测未来几周的销售情况，而非仅仅预测明天的销量，因此，需要的是预测未来的多个时间步骤。这种预测未来的多个时间步长的任务被称为多步时间序列预测(multi-step time series forecasting)。多步时间序列预测通常有四种主要的方法：

  • 多步递归预测(recursive multi-step forecasting)

  • 多步直接预测(direct multi-step forecasting)

  • 直接&递归融合预测(direct-recursive hybrid forecasting)

  • 多输出预测(multiple output forecasting)

下面我们会分别讲解这4种方法的原理，对比他们的性能，并在 SageMaker Notebook 中实现它们。可以在命令行执行下列命令，下载相关代码及数据集。

git clone https://github.com/multi-step-forecasting-blog-sample-code

技术交流

技术要学会分享、交流，不建议闭门造车。一个人可以走的很快、一堆人可以走的更远。

本文由粉丝群小伙伴的分享、总结。文章源码、数据、技术交流提升，均可加交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、添加微信号：dkl88194，备注：来自CSDN + 加群
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群

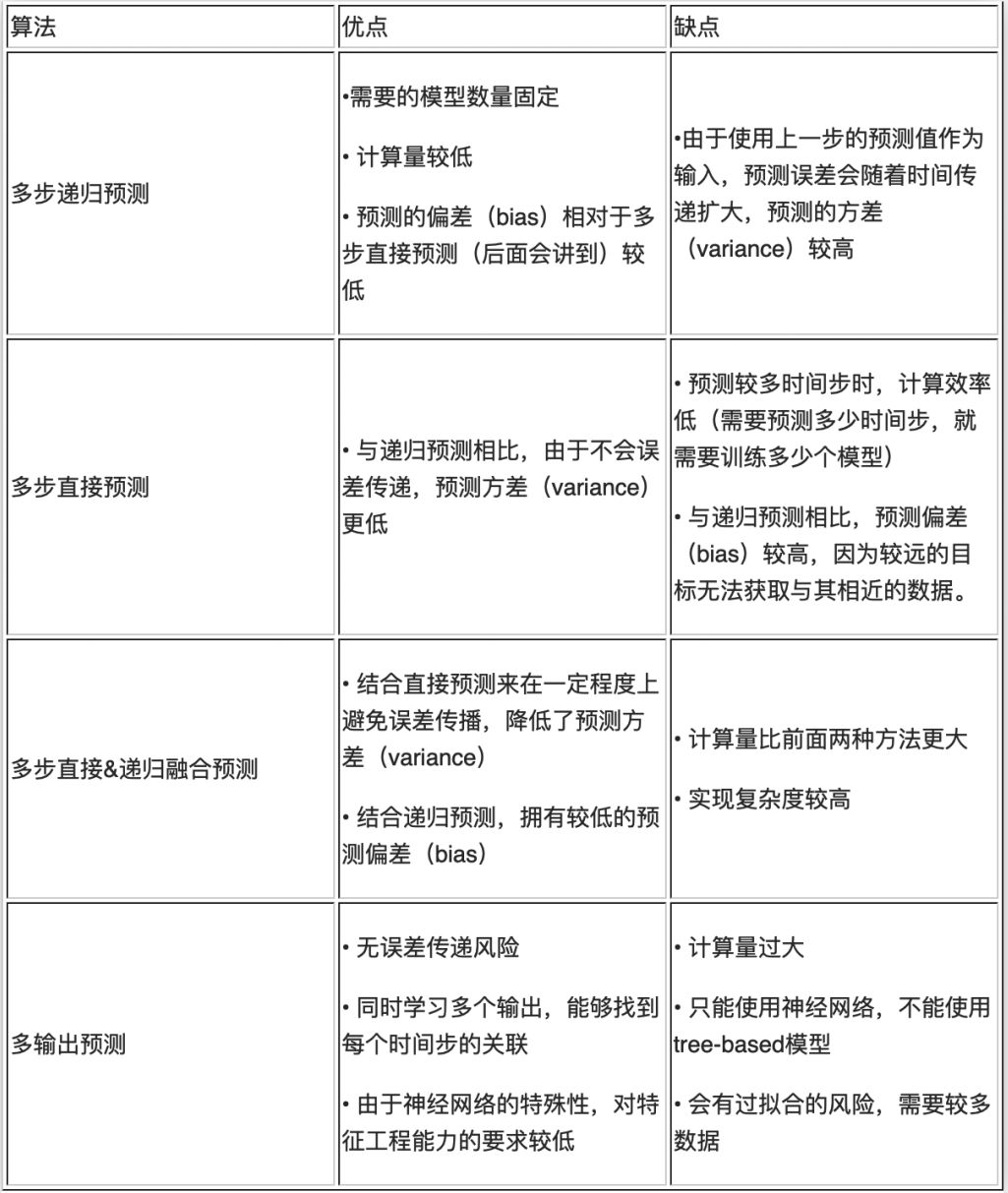
2 多步递归预测 (recursive multi-step forecasting)

多步递归预测在单步预测的基础上，把下一步的预测值作为输入，来进行迭代预测。需要注意的是：在多变量的多步回归分析中，由于存在外部变量作为输入，需要同时预测外部变量。多步递归的过程如下图所示：

图片

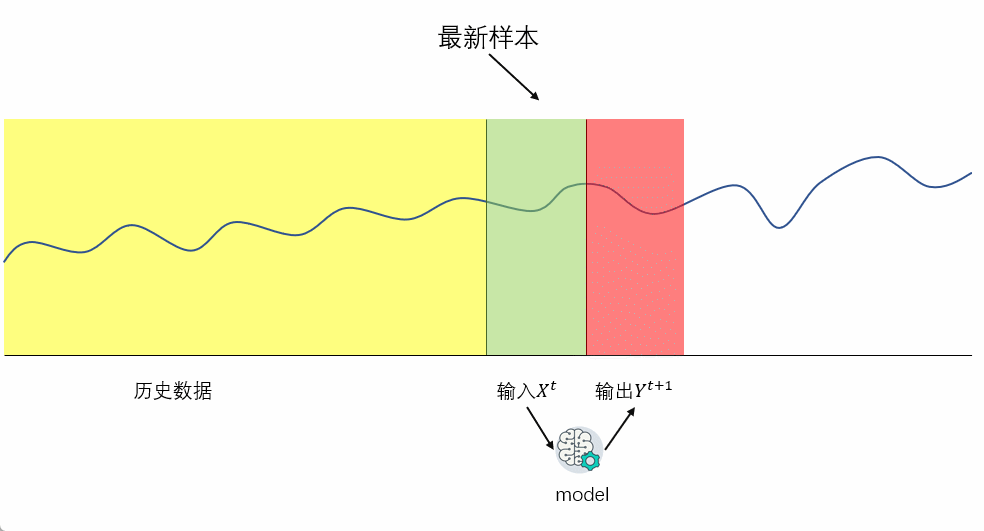
优点：

  • 需要的模型数量固定

  • 计算量较低

  • 预测的偏差(bias)相对于多步直接预测（后面会讲到）较低

缺点：
  • 由于使用上一步的预测值作为输入，预测误差会随着时间传递扩大，预测的方差(variance)较高

图片

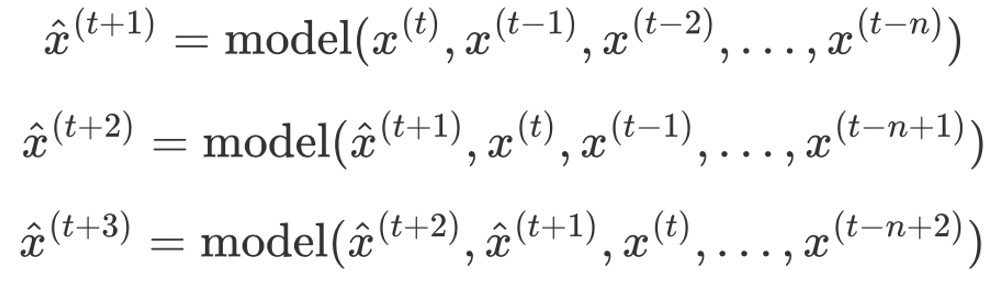
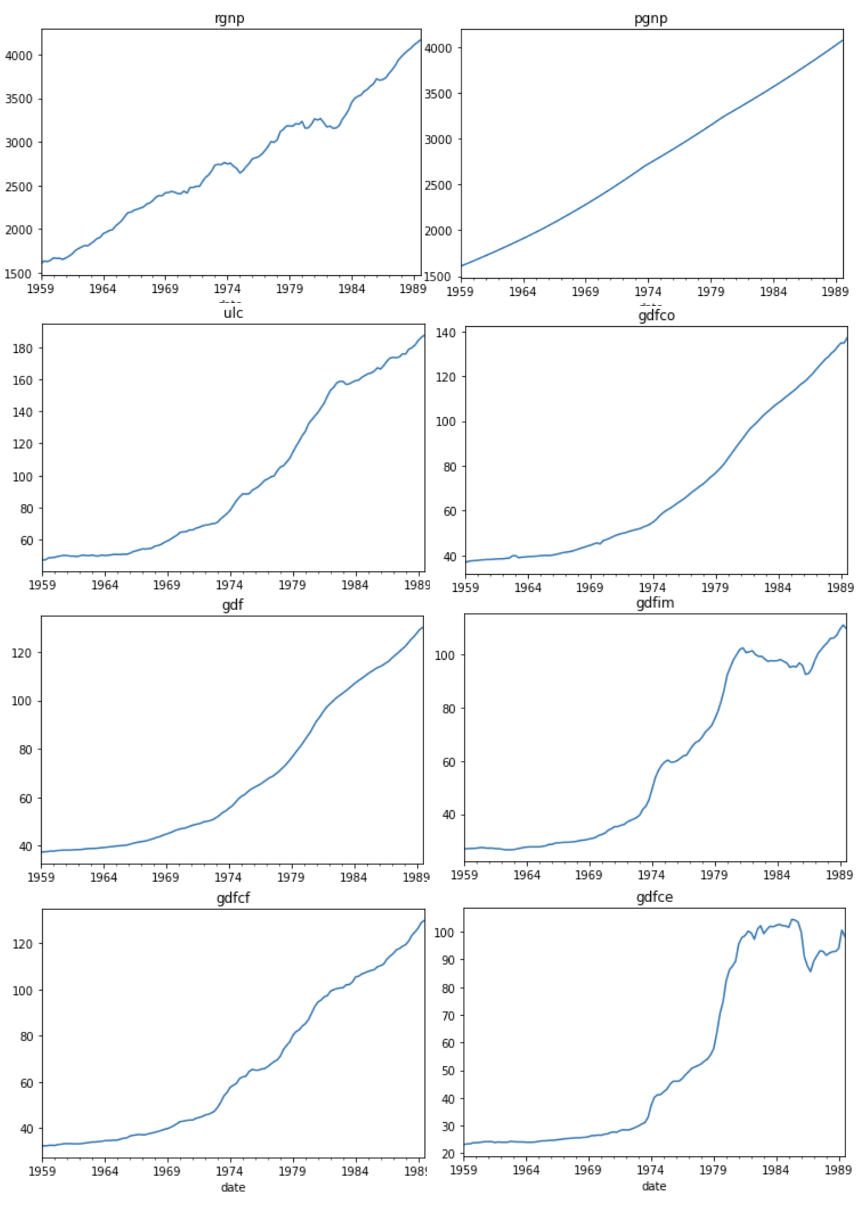
下面我们结合多变量回归分析，来实现多步递归预测。数据集涵盖1959年 Q1 至1988年 Q4 的工资数据。数据集共有123行和8列，列的定义：

  1. rgnp : 预测目标，实际 GNP(gross national product，国民生产总值)

  2. pgnp : 潜在 GNP

  3. ulc : 单位劳动成本

  4. gdfco : 不包括食物和能源在内的个人消费支出的固定权重平减指数

  5. gdf : 固定重量 GNP 缩减指数

  6. gdfim : 定量进口减缩指数

  7. gdfcf : 个人消费支出中食品的固定重量平减指数

  8. gdfce : 个人消费支出中能量的固定权重平减指数

在进行建模前，我们先查看一下每个变量的走势，可以看到8个变量均为向上趋势，各个变量间有一定相关性。此外，可以看到数据没有季节性(seasonality)，因此，我们在后续的建模过程中未加入季节性相关的处理。

图片

在编写代码前，首先需要安装所需的库。

! pip install lightgbm

我们的预测目标是 rgnp，也就是实际的国民生产总值。我们希望预测未来一年，也就是12个月中，每个月的国民生产总值。接下来，让我们进入代码部分。我们的代码使用的基础模型是 LightGBM，您也可以根据自己的需求选择其他任何回归算法。

首先，加载数据集：

import pandas as pd
import numpy as np
import lightgbm as lgb
from sklearn.metrics import mean_squared_error
from sklearn.multioutput import MultiOutputRegressor
数据获取：关注公众号:Python学习与数据挖掘 后台回复 多步时间序列预测
df = pd.read_csv('Raotbl6.csv')
# 将date作为索引
df['date'] = pd.to_datetime(df['date'])
df.index = df['date']
df.drop('date', axis=1, inplace=True)
以 8：2 来分割训练集与测试集
target = 'rgnp'X_train = df[: int(len(df) * 0.8)]
y_train = df[: int(len(df) * 0.8)]X_test = df[int(len(df) * 0.8) :]
y_test = df[int(len(df) * 0.8) :]

构建模型，由于迭代预测需要知道全部变量未来的值，因此模型除了预测目标变量，还要预测每一个变量。

MultiOutputRegressor 使用相同的 feature 来预测多个目标，通过该对象，可以针对每个目标训练出一个回归器。

model = MultiOutputRegressor(lgb.LGBMRegressor(objective='regression')).fit(X_train, y_train)

迭代预测，每次预测全部变量的未来值，共预测12次（一年）。

results = []
data = X_test
for i in range(12):data = pd.DataFrame(model.predict(data), columns=data.columns, index=data.index)results.append(data)
接下来，我们看一下预测结果，我们以MAE(mean average error)作为评价标准。
# make future targets
for i in range(12):df['rgnp_{}'.format(i)] = df['rgnp'].shift(-i)df.dropna(inplace=True)
df.drop('rgnp', axis=1, inplace=True)targets = [item for item in df.columns if 'rgnp' in item]X_train = df.drop(targets, axis=1)[: int(len(df) * 0.8)]
y_train = df[targets][: int(len(df) * 0.8)]X_test = df.drop(targets, axis=1)[int(len(df) * 0.8) :]
y_test = df[targets][int(len(df) * 0.8) :](y_test - pred).abs().mean()

图片

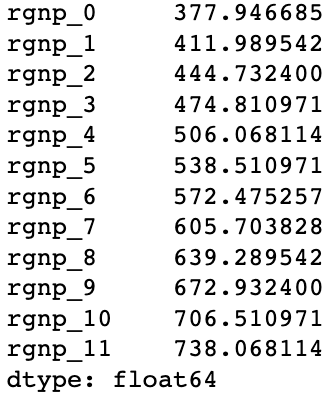
我们可以看到，随着预测距离逐渐变远，我们的预测准确率会变得越来越低。这个结果也是合理的，因为预测误差会不断向后传递。

3 多步直接预测(direct multi-step forecasting)

多步直接预测的逻辑是训练多个模型，每个模型负责预测未来一个时间步的值。

图片

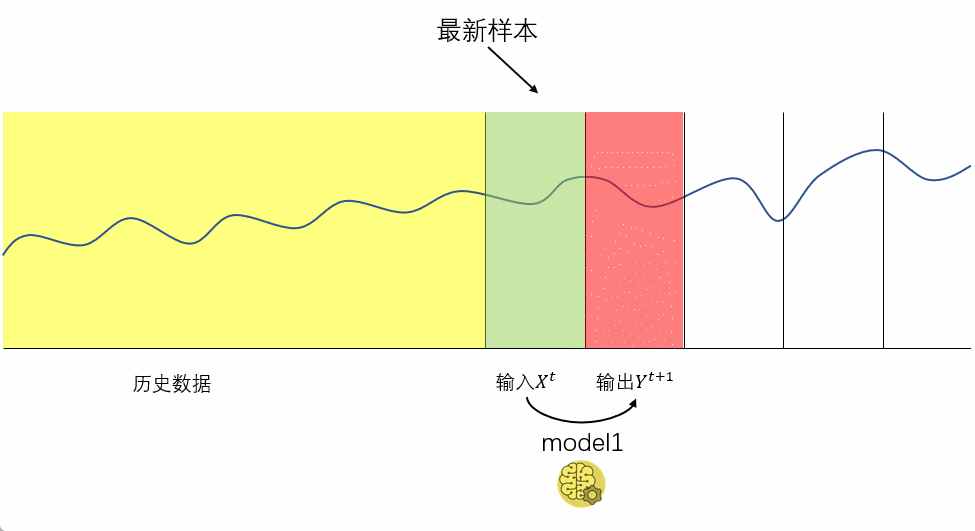
优点：
  • 与递归预测相比，由于不会误差传递，预测方差(variance)更低
缺点：

  • 预测较多时间步时，计算效率低（需要预测多少时间步，就需要训练多少个模型）

  • 与递归预测相比，预测偏差(bias)较高，因为较远的目标无法获取与其相近的数据

图片

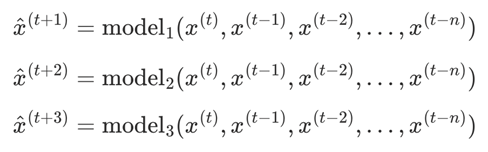
接下来，我们在同样的数据集上使用直接预测来进行多步时间序列分析。

使用同样的方法来加载数据：

import pandas as pd
import numpy as np
import lightgbm as lgb
from sklearn.metrics import mean_squared_error
from sklearn.multioutput import MultiOutputRegressor数据获取：关注公众号:Python学习与数据挖掘 后台回复 多步时间序列预测df = pd.read_csv('Raotbl6.csv')
df['date'] = pd.to_datetime(df['date'])
df.index = df['date']
df.drop('date', axis=1, inplace=True)
为每个未来的时间步创建一列
# make future targets
for i in range(12):df['rgnp_{}'.format(i)] = df['rgnp'].shift(-i-1)df.dropna(inplace=True)

分割训练集与测试集：

targets = [item for item in df.columns if 'rgnp_' in item]X_train = df.drop(targets, axis=1)[: int(len(df) * 0.8)]
y_train = df[targets][: int(len(df) * 0.8)]X_test = df.drop(targets, axis=1)[int(len(df) * 0.8) :]
y_test = df[targets][int(len(df) * 0.8) :]model = MultiOutputRegressor(lgb.LGBMRegressor(objective='regression')).fit(X_train, y_train)

查看预测结果：

pred = pd.DataFrame(model.predict(X_test), columns=targets)
pred.index = y_test.index
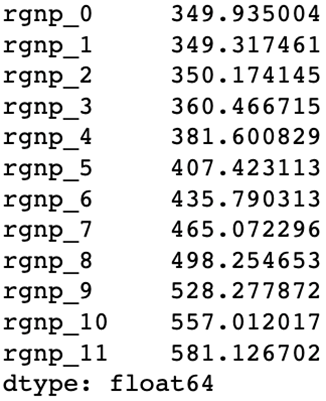
(y_test - pred).abs().mean()

我们可以看到，预测的误差也是随着时间步的拉远变大，但与递归预测相比，误差的损失变得更小了。这是直接预测算法的优越性，由于 variance 更低，预测远距离时间步会更准确。

图片

4 多步直接&递归融合预测 (direct-recursive hybrid forecasting)

多步递归预测与多步直接预测各有千秋，递归预测的 bias 低，但 variance 高。而直接预测则是 variance 低，但 bias 高。

那么是否有一种方法可以结合两者呢？答案是肯定的，这种方法叫做直接&递归融合预测。

直接&递归融合预测的具体实施方法有很多种，下面我们以其中一种方法举例：

  1. 创建递归模型

  2. 创建直接预测模型，但预测模型的输入还包括递归模型在先前时间步中所做的预测作为输入值

图片

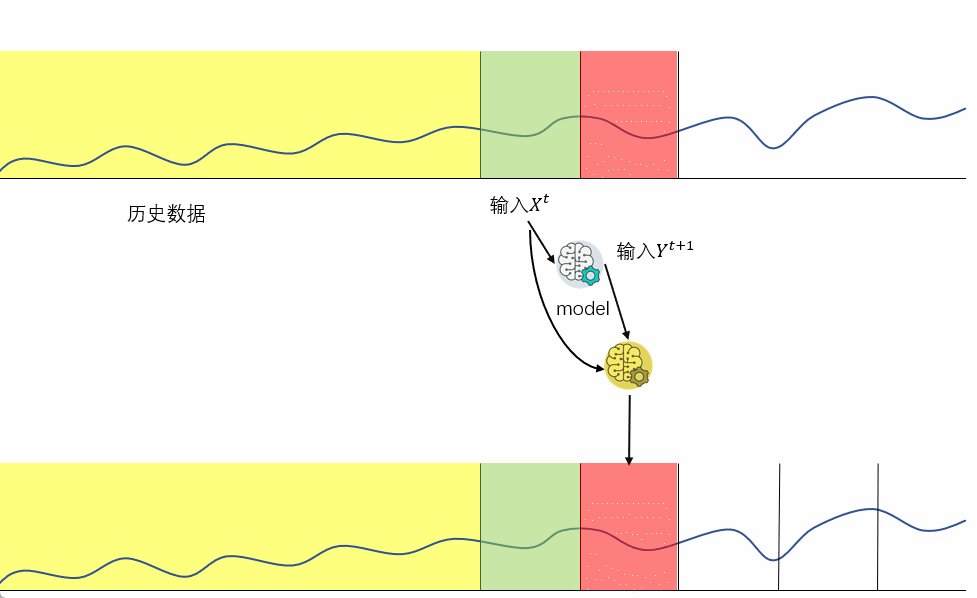
优点：

  • 结合直接预测来在一定程度上避免误差传播，降低了预测方差（variance）

  • 结合递归预测，拥有较低的预测偏差（bias）

缺点：

  • 计算量比前面两种方法更大

  • 实现复杂度较高

图片

同样的，我们先加载数据集：

import pandas as pd
import numpy as np
import lightgbm as lgb
from sklearn.metrics import mean_squared_error
from sklearn.multioutput import MultiOutputRegressordf = pd.read_csv('Raotbl6.csv')
df['date'] = pd.to_datetime(df['date'])
df.index = df['date']
df.drop('date', axis=1, inplace=True)

训练递归模型：

target = 'rgnp'X_train = df[: int(len(df) * 0.8)].iloc[:-1]
y_train = df[: int(len(df) * 0.8)].shift(-1).dropna()X_test = df[int(len(df) * 0.8) :].iloc[:-1]
y_test = df[int(len(df) * 0.8) :].shift(-1).dropna()model = MultiOutputRegressor(lgb.LGBMRegressor(objective='regression')).fit(X_train, y_train)

取得递归模型的预测结果：

results = []
data = X_test
for i in range(12):data = pd.DataFrame(model.predict(data), columns=data.columns, index=data.index)results.append(data)

为直接模型构建基础特征：

# make future targets 
for i in range(12):df['rgnp_{}'.format(i+1)] = df['rgnp'].shift(-i-1)df.dropna(inplace=True)targets = [item for item in df.columns if 'rgnp_' in item]X_train = df.drop(targets, axis=1)[: int(len(df) * 0.8)]
y_train = df[targets][: int(len(df) * 0.8)]X_test = df.drop(targets, axis=1)[int(len(df) * 0.8) :]
y_test = df[targets][int(len(df) * 0.8) :]

训练直接模型，每次把上一步的递归模型的预测值也作为特征来训练模型。

models = []
for i in range(1, 13):model = lgb.LGBMRegressor(objective='regression').fit(X_train, y_train['rgnp_{}'.format(i)])X_train['rgnp_{}'.format(i)] = y_train['rgnp_{}'.format(i)]models.append(model)

使用直接模型来做预测：

final_results = []for i in range(12):final_results.append(models[i].predict(X_test))X_test['rgnp_{}'.format(i + 1)] = results[i]['rgnp']

图片

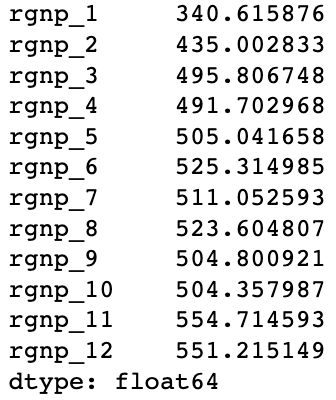
我们可以看到，递归&直接预测融合模型的误差要低于递归预测或直接预测的模型。当然，基于 no free lunch 原则，我们无法完全确定融合方法要好于单独方法。

5 多输出预测 (multiple output forecasting)

前面3种方法中，我们可以计算出输入间的相关性，但无法计算输出间的相关性。而多输出预测，则是使用一个神经网络模型预测整个预测序列，每个权重对每个输出都有影响，因此模型会同时学习到输入与输出的相关性。

优点：

  • 不会有误差传递风险

  • 同时学习多个输出，能够找到每个时间步的关联

  • 由于神经网络的特殊性，对特征工程能力的要求较低

缺点：

  • 计算量过大

  • 只能使用神经网络，不能使用 tree-based 模型

  • 会有过拟合的风险，需要较多数据

图片

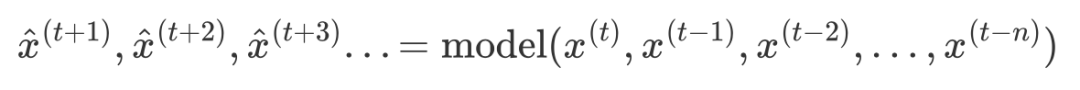
接下来以 PyTorch 为例，来进行预测。本案例使用 SageMaker Notebook 的 conda_pytorch_p38 kernel，无需自行安装 PyTorch 库。

图片

import pandas as pdimport torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
import torch.optim as optimimport pandas as pd
import numpy as np
import lightgbm as lgb
from sklearn.metrics import mean_squared_errordf = pd.read_csv('Raotbl6.csv')
df['date'] = pd.to_datetime(df['date'])
df.index = df['date']
df.drop('date', axis=1, inplace=True)# make future targets
for i in range(12):df['rgnp_{}'.format(i)] = df['rgnp'].shift(-i-1)df.dropna(inplace=True)targets = [item for item in df.columns if 'rgnp_' in item]X_train = df.drop(targets, axis=1)[: int(len(df) * 0.8)]
y_train = df[targets][: int(len(df) * 0.8)]X_test = df.drop(targets, axis=1)[int(len(df) * 0.8) :]
y_test = df[targets][int(len(df) * 0.8) :]

构建数据集类，用于训练数据。

class Raotbl6Dataset(Dataset):"""Face Landmarks dataset."""def __init__(self, X_train, y_train):self.X_train = X_trainself.y_train = y_traindef __len__(self):return len(self.X_train)def __getitem__(self, idx):if torch.is_tensor(idx):idx = idx.tolist()X = torch.Tensor(self.X_train.iloc[idx].values)y = torch.Tensor(self.y_train.iloc[idx].values)return X, y

构建模型类，由于数据集非常小，所以只使用一个隐含层的神经网络。

class Model(nn.Module):def __init__(self, in_feats, out_feats=12, hidden_units=32):super(Model, self).__init__()self.net = nn.Sequential(nn.Linear(in_feats, hidden_units),nn.ReLU(),nn.Linear(hidden_units, out_feats))def forward(self, x):return self.net(x)

训练模型，由于数据集的数据量太少，因此训练500轮来尽量提升模型性能。

NUM_EPOCHS = 500
LEARNING_RATE = 2e-4
device = 'cuda' if torch.cuda.is_available() else 'cpu'dataset = Raotbl6Dataset(X_train, y_train)
dataloader = DataLoader(dataset,batch_size=32, shuffle=True)
criterion = torch.nn. MSELoss()model = Model(8).to(device)
opt = optim.Adam(model.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999))for epoch in range(NUM_EPOCHS):model.train()for batch_idx, (X, y) in enumerate(dataloader):X, y = X.to(device), y.to(device)pred = model(X)loss = criterion(y, pred)model.zero_grad()loss.backward()opt.step()print(f"Epoch [{epoch}/{NUM_EPOCHS}] \ERROR: {loss:.4f}")pred = pd.DataFrame(model(torch.Tensor(X_test.values).to(device)), columns=y_test.columns, index=y_test.index
(y_test - pred).abs().mean()

图片

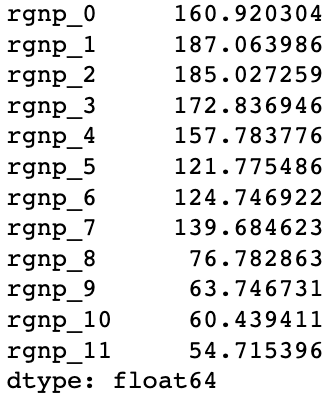
可以看到，由于神经网络足够简单，即使只有100条数据并训练了500轮，也并没有过拟合，它的性能也超过前面3种方法较多，这其中也与前面3种方法没有花费时间调参有关。

6 总结

本篇文章中，我们展示了4种基于机器学习进行多步时间序列预测的方法。下列表格中分别列出了各个算法的优缺点。

图片

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/19061.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

史上最细接口测试详解，接口测试从0到1实施，一篇打通...

史上最细接口测试详解，接口测试从0到1实施，一篇打通...

目录：导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结（尾部小惊喜） 前言 1、接口测试描述定…
阅读更多...
Mysql之进阶宝典系列-视图

Mysql之进阶宝典系列-视图

Mysql之进阶宝典系列-视图 一、视图是什么(what) 视图本质上是一个虚表，在数据库中不实际存在，它的所有数据来源于查询中所使用的表的数据，而且是在视图调用过程中动态生成的。视图只保存了SQL查询的逻辑，不保存SQL查询的结果。 …
阅读更多...
springboot家具商城系统

springboot家具商城系统

开发语言：Java 框架：springboot JDK版本：JDK1.8 服务器：tomcat7 数据库：mysql 5.7（一定要5.7版本） 数据库工具：Navicat11 开发软件：eclipse/myeclipse/idea Maven…
阅读更多...
测试必备的15个docker命令，你都掌握了吗

测试必备的15个docker命令，你都掌握了吗

1、Docker容器信息 ##查看docker容器版本docker version##查看docker容器信息docker info##查看docker容器帮助docker --help 2、镜像操作 提示：对于镜像的操作可使用镜像名、镜像长ID和短ID。 2.1、镜像查看 ##列出本地imagesdocker images##含中间映像层docke…
阅读更多...
SAP MESSAGE ID LB31的问题和解决办法

SAP MESSAGE ID LB31的问题和解决办法

外协采购订单判退时报错 EA 返回交货(原因)-> 3700006717 /00009 (0000) 1 EA 不正确过帐返回给供应商，错误信息:对所需数量 XXXXXX00003122，1.000 PCS 仍然未清LB 31 搜索到lb31是和批次相关的错误 https://www.michaelmanagement.com/sap-error-mes…
阅读更多...
OSPFv2基础02_工作原理

OSPFv2基础02_工作原理

目录 1.OSPF接口状态 2.OSPF邻居状态 2.1 OSPF邻居状态类型 2.2 广播网络OSPF邻接关系建立 3.Router ID（路由器ID）选举 4.DR和BDR选举 4.1 为什么引入DR和BDR？ 4.2 DR和BDR的作用 4.3 DR和BDR选举过程 4.4 DR和BDR选举原则 5.OSPF路…
阅读更多...
Vue3+Vite+Pinia+Naive后台管理系统搭建之二：scss 的安装和使用

Vue3+Vite+Pinia+Naive后台管理系统搭建之二：scss 的安装和使用

前言 如果对 vue3 的语法不熟悉的，可以移步 Vue3.0 基础入门，快速入门。 1. 安装依赖 yarn add sass -D // or npm install sass -D 2. 页面样式初始化 reset.scss /* 新建 src/assets/style/reset.scss */ /* 页面样式初始化 */ html, body, div, s…
阅读更多...
常见的BUG---1、虚拟机启动之后，突然发现没有ens33网卡

常见的BUG---1、虚拟机启动之后，突然发现没有ens33网卡

1、问题描述 今天一开启虚拟机，发现用XShell连接不上我的一台虚拟机，其他虚拟机是正常可以连接的，我稍微看了一下XShell的配置和Windows中的映射文件（hosts），都没有啥问题，然后我就知道应该是虚…
阅读更多...
SSM学习笔记-------Spring（二）

SSM学习笔记-------Spring（二）

SSM学习笔记-------Spring（二） Spring_day021、IOC/DI配置管理第三方bean1.1 案例:数据源对象管理1.1.1 环境准备1.1.2 思路分析1.1.3 实现Druid管理步骤1:导入druid的依赖步骤2:配置第三方bean步骤3:从IOC容器中获取对应的bean对象步骤4:运行程序 1.1.4…
阅读更多...
CASAIM与大疆达成全自动化测量技术合作，CASAIM IS全自动化蓝光测量仪实现无人机叶片全尺寸检测及质量控制

CASAIM与大疆达成全自动化测量技术合作，CASAIM IS全自动化蓝光测量仪实现无人机叶片全尺寸检测及质量控制

近期，CASAIM与大疆达成全自动化测量技术合作，CASAIM IS全自动化蓝光测量仪实现无人机叶片全尺寸检测及质量控制。 无人机行业在过去几年里取得了迅猛发展，大疆是全球领先的无人飞行器控制系统及无人机解决方案的研发商和生产商，客…
阅读更多...
天津良心web前端培训学校品牌汇总（Web前端的起步薪资）

天津良心web前端培训学校品牌汇总（Web前端的起步薪资）

现在很多小伙伴想要了解web前端开发技术知识，但是不知道现在学习web前端值不值得，会有很多小伙伴开始犹豫学不学，学完能不能找到工作，那下面小编就通过下面三点，来给大家简单分析一下web行业，以及要不要报班…
阅读更多...
需要为您的网站配置CDN的九大理由

需要为您的网站配置CDN的九大理由

所有的网站访问者都期望能够给用户提供快速高效的访问和使用体验，没有延迟或网站性能问题意味着更多的顾客和访问量。然而高流量和覆盖全球的网站意味着网站管理者面临着延迟增加和页面加载时间缓慢的挑战，这可能会导致业务损失。据统计，四分…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023