最长公共子序列

力扣链接

• 单个数组的子序列问题 – dp[i] -- 以nums[i] 为结尾的所有子序列中, xxx xxx. 然后状态转移方程根据 最后一个位置的归属问题进行讨论

• 两个数组的子序列问题 – 以小见大, 分别分析nums1中的一个区间 和 nums2的一个区间进行讨 --> dp[i][j] -- nums1中的[0, i] 区间 以及 nums2中的 [0, j]区间内的所有子序列的组合中, 公共子序列的最大长度

• 状态转移方程 – 最后一个位置的具体情况
  

• 遍历顺序
  

• 初始化
  需要使用左上角的情况 ⇒ dp表可以多开一行, 多开一列
  但是dp表中使用原 nums1 和 nums2的情况就会出现偏差, 解决方法

  1. 访问nums1 和 nums2里面的情况, 就要 －1
  2. 可以在nums1, nums2前面添加一个 空格 ⇒ 使得dp表中的下标 和 nums1 和 nums2中的下标一致化

  ⇒ 这样初始化就方便很多 , 都初始化为 0

• 返回值 — dp[i][j] -- nums1中的[0, i] 区间 以及 nums2中的 [0, j]区间内的所有子序列的组合中, 公共子序列的最大长度 ⇒ 返回 dp[m][n]

1. 访问 -1

class Solution {
public:int longestCommonSubsequence(string nums1, string nums2) {int m = nums1.size();int n  = nums2.size();vector<vector<int>> dp(m+1, vector<int>(n+1));for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){// 访问, -1if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = max(dp[i][j-1], dp[i-1][j]);}}}return dp[m][n];}
};

2. 添加空格

class Solution {
public:int longestCommonSubsequence(string nums1, string nums2) {int m = nums1.size();int n  = nums2.size();vector<vector<int>> dp(m+1, vector<int>(n+1));// 访问, 添加空格nums1 = ' ' + nums1;nums2 = ' ' + nums2;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(nums1[i] == nums2[j]){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = max(dp[i][j-1], dp[i-1][j]);}}}return dp[m][n];}
};

---

不相交的线

力扣链接

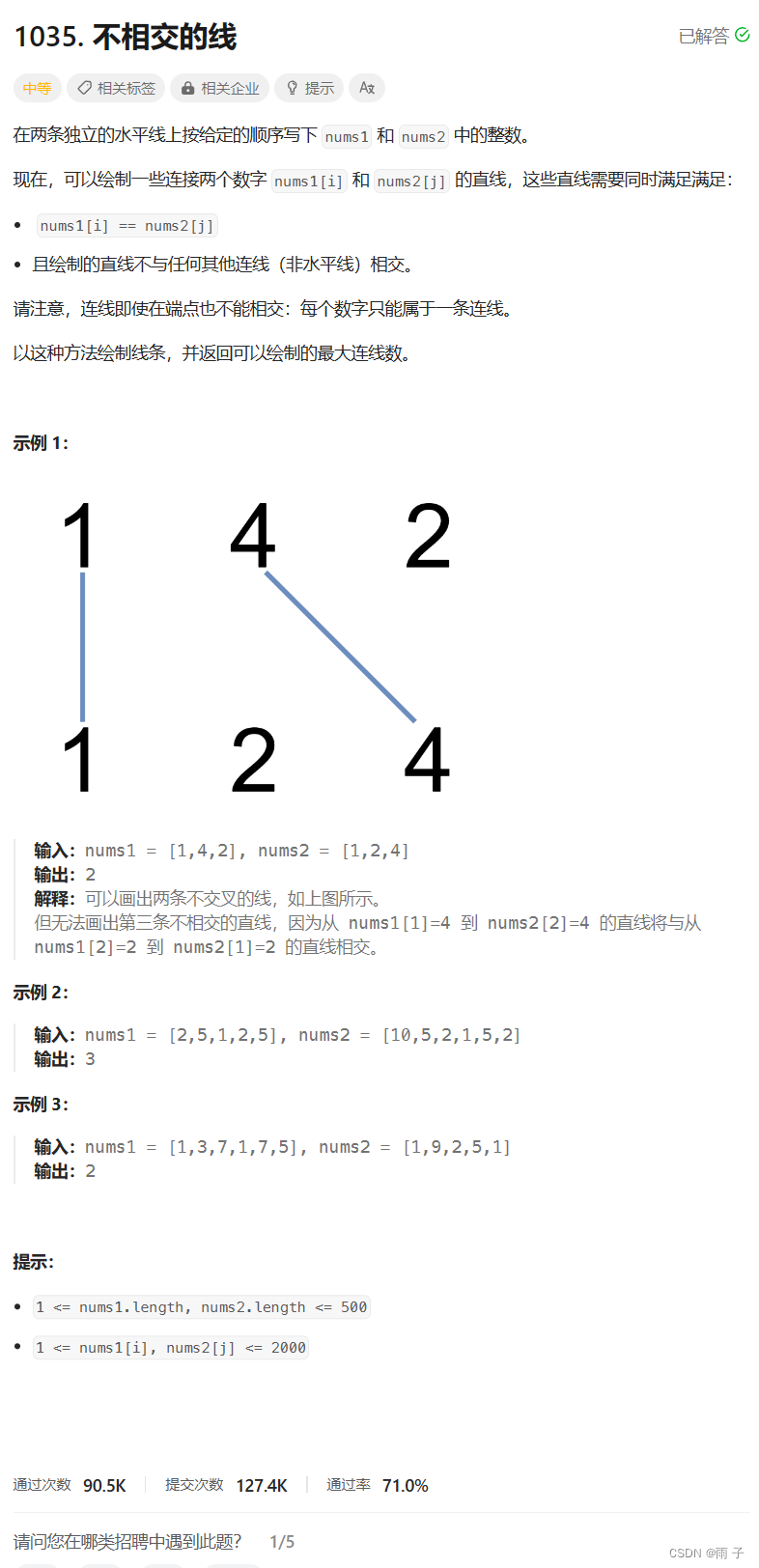
这题的是 最长公共子序列 的变种题目, 求区间内的公共子序列的最长长度

• 两个数组的子序列问题 – 以小见大, 分别分析nums1中的一个区间 和 nums2的一个区间进行讨 --> dp[i][j] -- nums1中的[0, i] 区间 以及 nums2中的 [0, j]区间内的所有子序列的组合中, 公共子序列的最大长度

• 状态转移方程 – 最后一个位置的具体情况
  

• 遍历顺序
  

• 初始化
  需要使用左上角的情况 ⇒ dp表可以多开一行, 多开一列
  但是dp表中使用原 nums1 和 nums2的情况就会出现偏差, 解决方法

  1. 访问nums1 和 nums2里面的情况, 就要 －1
  2. 可以在nums1, nums2前面添加一个 空格 ⇒ 使得dp表中的下标 和 nums1 和 nums2中的下标一致化

  ⇒ 这样初始化就方便很多 , 都初始化为 0

• 返回值 — dp[i][j] -- nums1中的[0, i] 区间 以及 nums2中的 [0, j]区间内的所有子序列的组合中, 公共子序列的最大长度 ⇒ 返回 dp[m][n]

class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size();int n = nums2.size();vector<vector<int>> dp(m+1, vector<int>(n+1));for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}}}return dp[m][n];}
};

---

日出而作，日入而息。
凿井而饮，耕田而食。
帝力于我何有哉？
— — 《击壤歌》