文章目录
- 上一篇
- 哈夫曼编码
- 单源最短路
- 最小生成树
- Kruskal算法
- Prim算法
- 多机调度问题
- 下一篇
上一篇
算法设计与分析复习–贪心(一)
哈夫曼编码
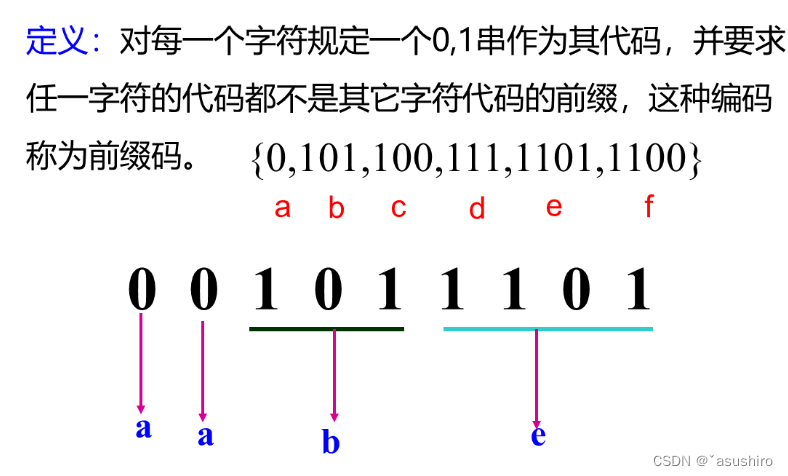
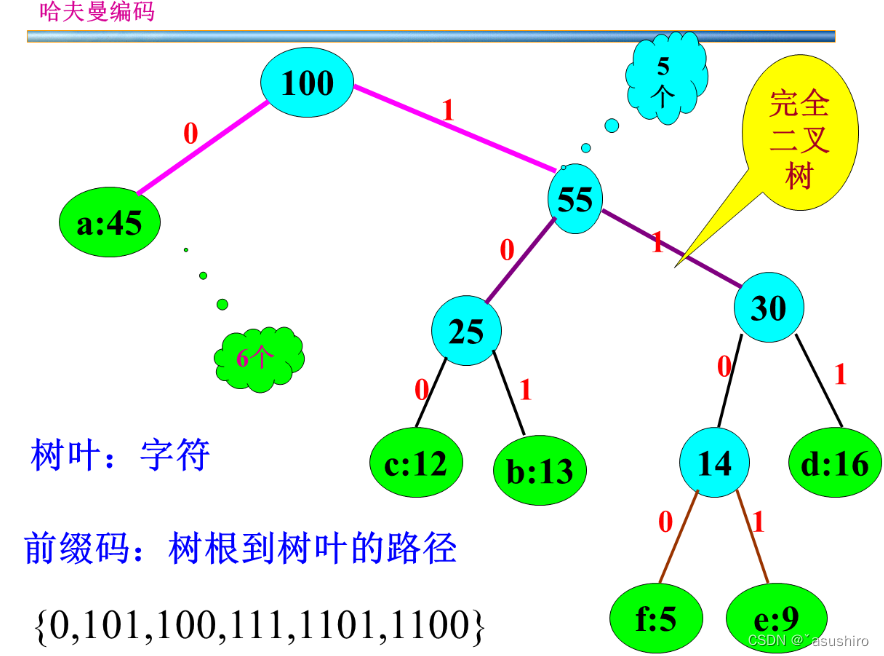
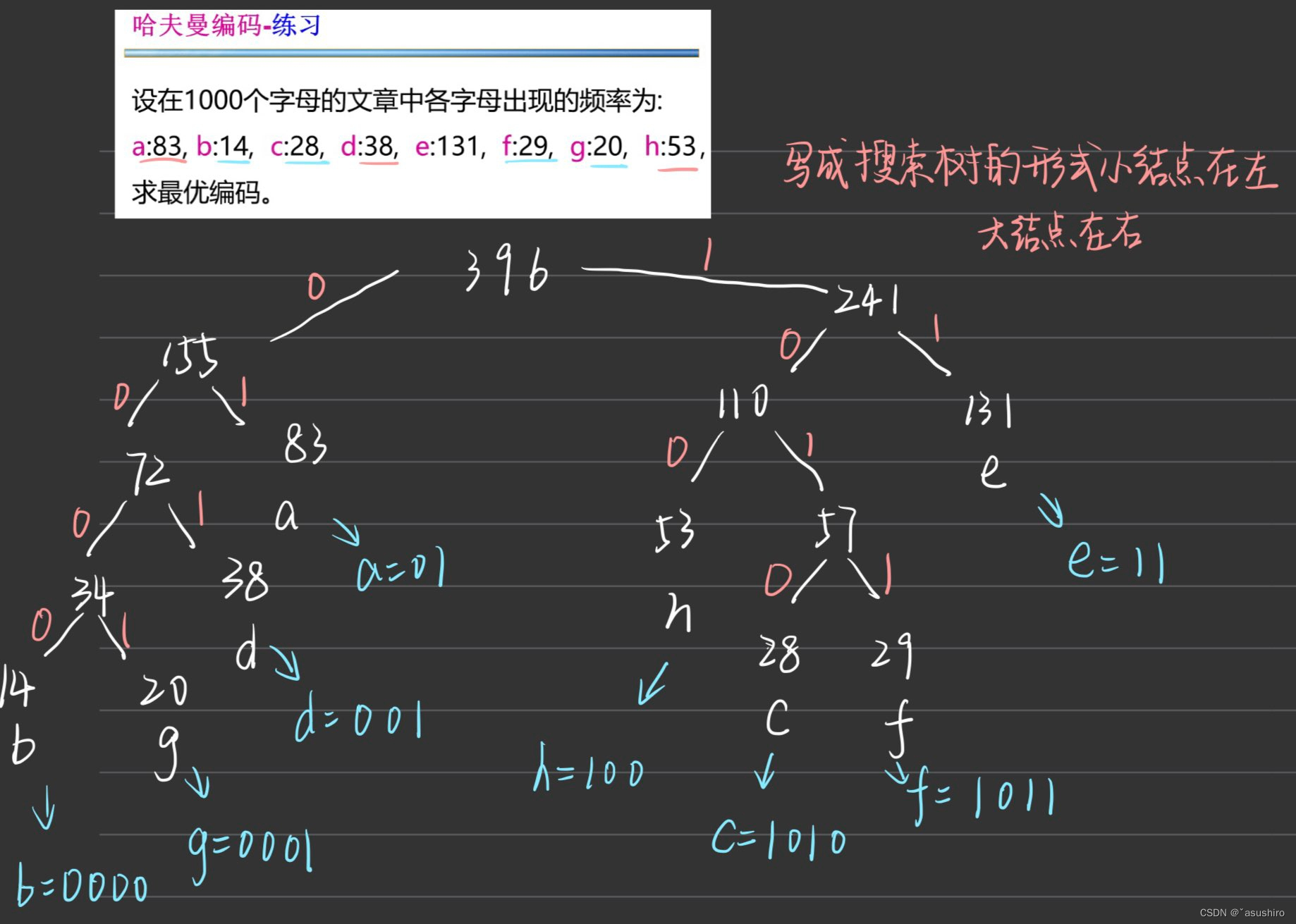
产生这种前缀码的方式称为哈夫曼树
哈夫曼树相关习题AcWing 148. 合并果子
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>using namespace std;const int N = 10010;int n;
priority_queue<int, vector<int>, greater<int> > heap;int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++){int x;scanf("%d", &x);heap.push(x);}int res = 0;while (heap.size() > 1){int x = 0;x += heap.top(); heap.pop();x += heap.top(); heap.pop();heap.push(x);res += x;}printf("%d", res);return 0;
}
单源最短路
最短路问题
Dijkstra方法

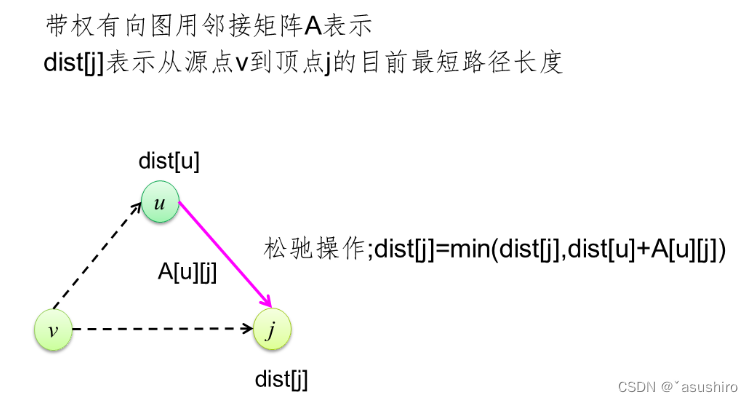
稠密图下
AcWing 849. Dijkstra求最短路 I
使用邻接矩阵来存
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 510;int g[N][N], n, m;
int dist[N];
bool st[N];int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;//这里不能初始化st[1]因为此时还没拓展边for (int i = 1; i < n; i ++){int t = -1;for (int j = 1; j <= n; j ++)if (!st[j] && (t == -1 || dist[j] < dist[t]))t = j;st[t] = true;//找到连接当前结点的最短的一条边了for (int j = 1; j <= n; j ++)dist[j] = min(dist[j], dist[t] + g[t][j]);//松弛操作}if (dist[n] > 0x3f3f3f3f >> 1) return -1;else return dist[n];
}int main()
{memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c);}printf("%d", dijkstra());return 0;
}
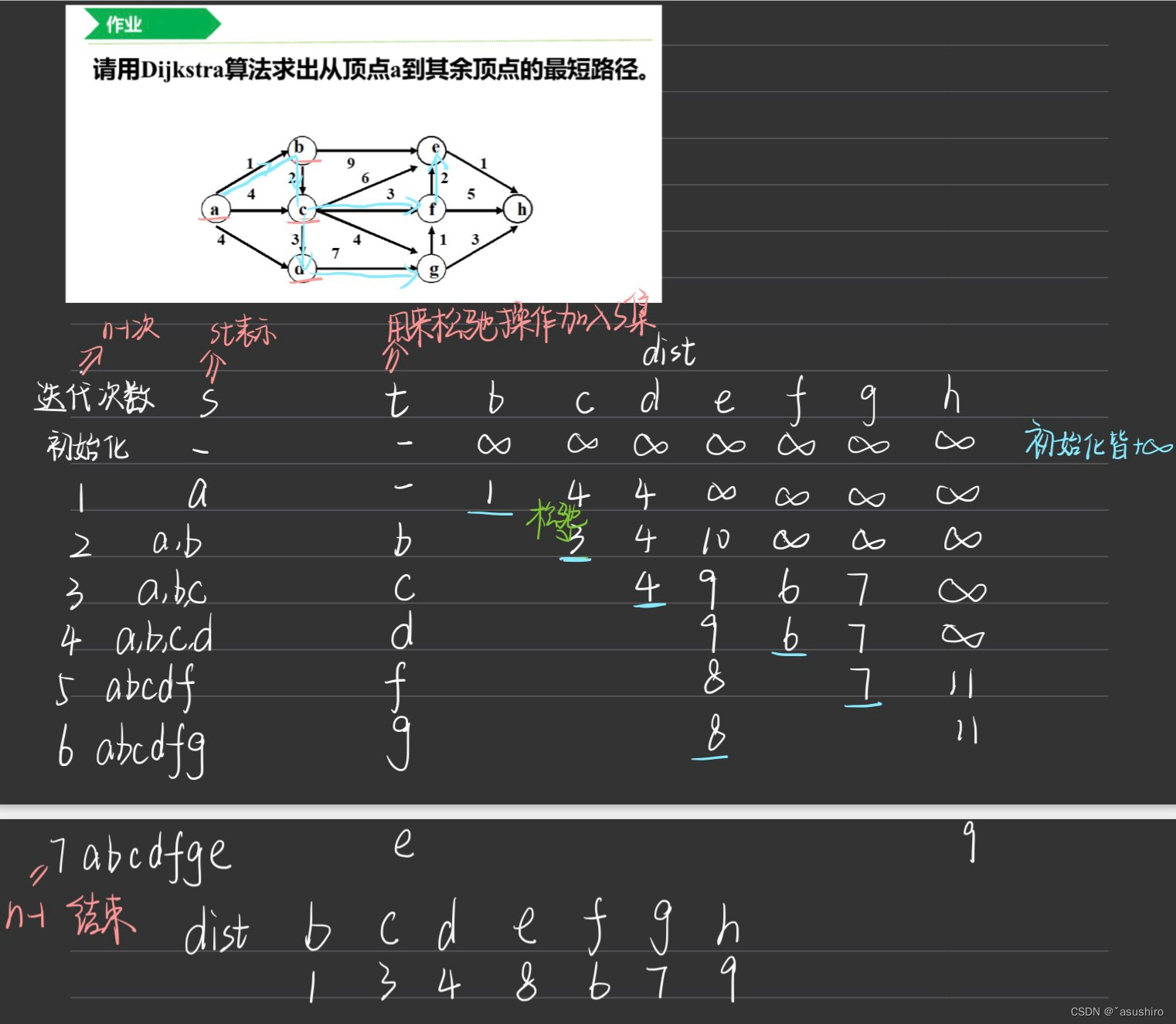
最小生成树
问题描述:设G = (V, E)是无向连通带权图。E中每条边(v, w)的权为c[v][w]。最小生成树问题就是要在G的所有生成树中,找到权值最小的那颗生成树。
最小生成树与二分图
up讲解
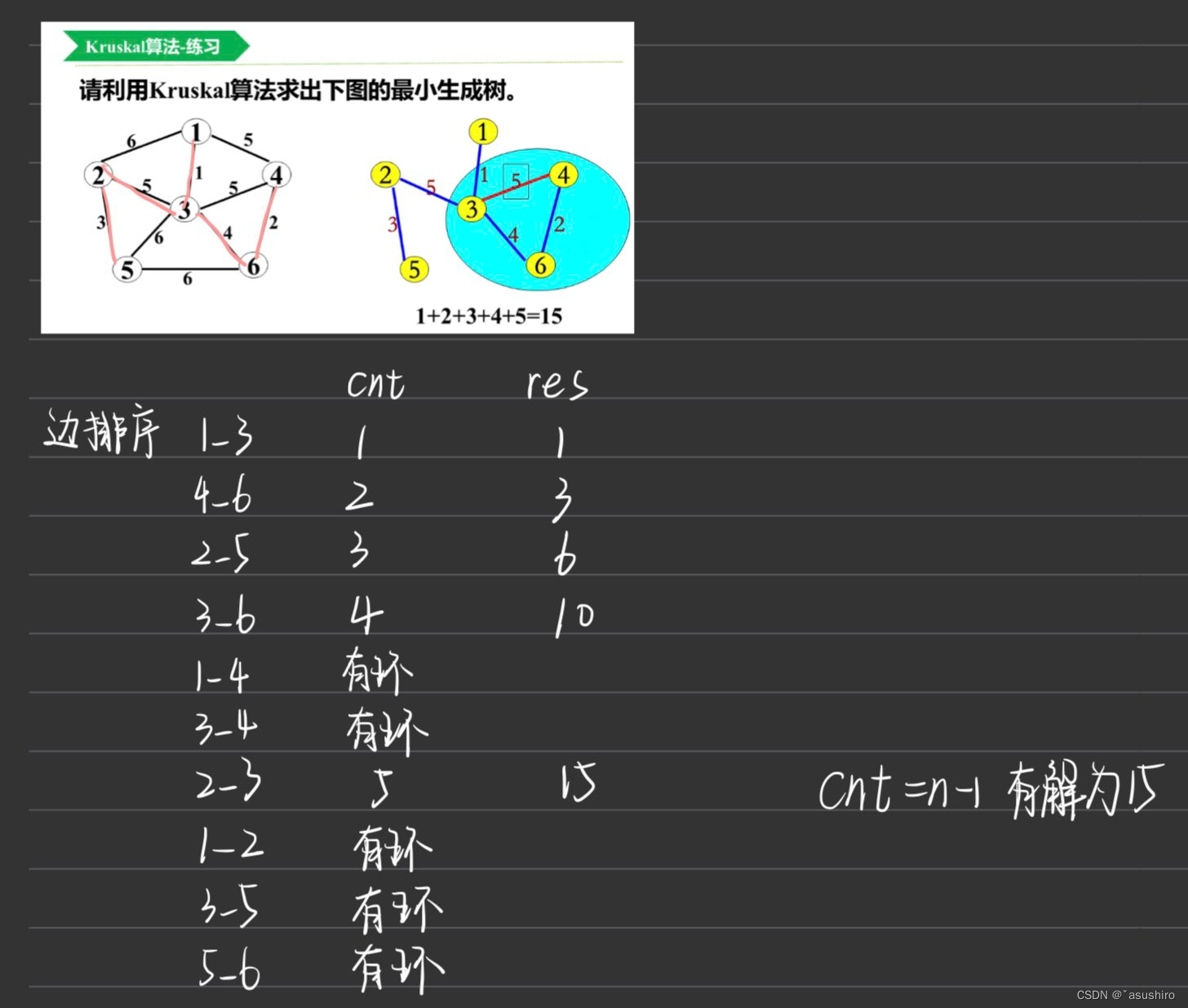
Kruskal算法
AcWing 859. Kruskal算法求最小生成树

从边的角度生成最小生成树,将边按照从小到大排序,并一次回放到结点集中,在进行判断是否有产生环,如果没有产生环就说明这个边的添加是可行的,直至添加n - 1个边,否则不能生成
判断是否有环产生使用并查集
适用于稀疏图,由于处理的是边的信息所以定义这个结构体
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010, M = 200010;// 边较少是稀疏图struct edge
{int a, b, c;
}e[M];int n, m, f[N];bool cmp(edge x, edge y)
{return x.c < y.c;
}int find(int x)
{if (x != f[x]) f[x] = find(f[x]);return f[x];
}void kruskal()
{sort(e, e + m, cmp);int res = 0, cnt = 0;for (int i = 0; i < m; i ++){int a = e[i].a, b = e[i].b, c = e[i].c;a = find(a), b = find(b);//并查集至少需要将两个点find一次,不如直接记下来if (a != b){f[a] = b;res += c;cnt ++;}}if (cnt < n - 1) puts("impossible");else printf("%d", res);
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++) f[i] = i; for (int i = 0; i < m; i ++) {scanf("%d%d%d", &e[i].a, &e[i].b, &e[i].c);}kruskal();return 0;
}
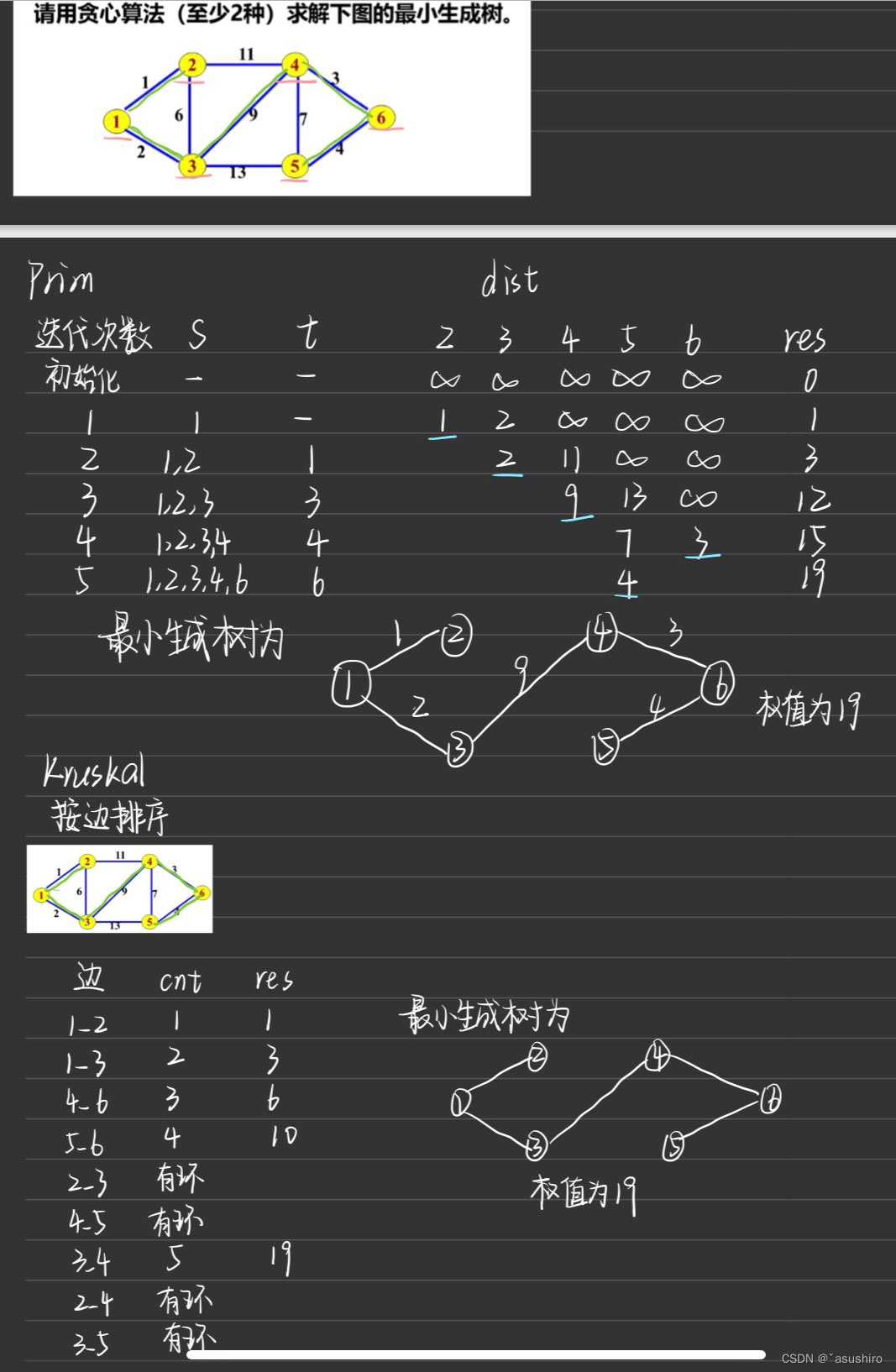
Prim算法
AcWing 858. Prim算法求最小生成树

将顶点集分为已选顶点集合和未选顶点集合,然后优先选择连接两个集合的权值最小的边
适用于稠密图,用邻接矩阵存的
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 510;int g[N][N], n, m;
int dist[N];
bool st[N];void prim()
{memset(dist, 0x3f, sizeof dist);int res = 0;for (int i = 0; i < n; i ++){int t = -1;for (int j = 1; j <= n; j ++)if (!st[j] && (t == -1 || dist[j] < dist[t]))t = j;st[t] = true;//第一个结点不做处理if (i && dist[t] == 0x3f3f3f3f){// 不连通puts("impossible");return;}if (i) res += dist[t];//加权重for (int j = 1; j <= n; j ++)dist[j] = min(dist[j], g[t][j]);//和dijkstra的区别,算的不是从起点到的距离而是两个点的距离,所以不加}printf("%d", res);}int main()
{memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);//无权图两边都要}prim();return 0;
}
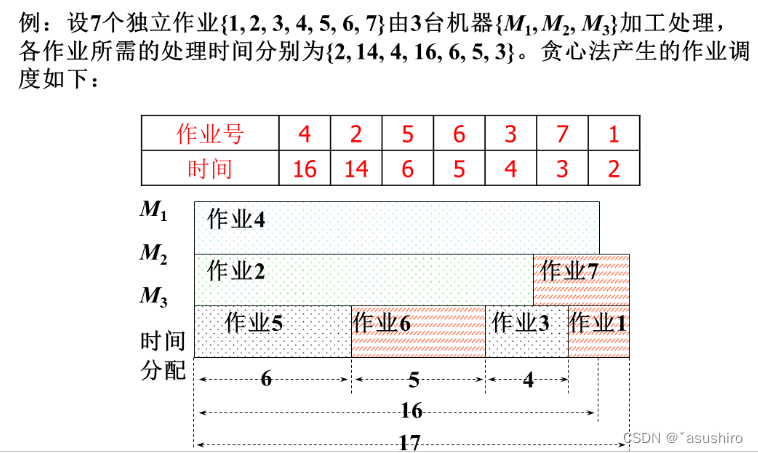
多机调度问题
设有n个独立的作业{1, 2, …,n}, 由m台相同的机器{ M 1 , M 2 , . . . , M m M_1, M_2, ..., M_m M1,M2,...,Mm}进行加工处理,作业 i i i 所需的处理时间为 t i t_i ti(1 <= i <= n),每个作业均可在任何一台机器上加工处理, 但不可间断、拆分。要求给出一种作业调度方案 ,使得n个作业在尽可能短的时间内被m个机器加工完成。
贪心策略:采取最长处理时间作业优先
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>using namespace std;
typedef pair<int, int> PII;const int N = 100010;int a[N], n, m;
priority_queue<PII, vector<PII>, greater<PII> > heap;bool cmp(int x, int y)
{return x > y;
}int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i ++) scanf("%d", &a[i]);for (int i = 1; i <= m; i ++) heap.push({0, i});sort(a, a + n, cmp);int res = 0;for (int i = 0; i < n; i ++){auto t = heap.top();heap.pop();t.first += a[i];res = max(res, t.first);heap.push(t);}printf("%d", res);return 0;
}
下一篇
未完待续