曲线拟合是数据分析和数学建模领域中广泛使用的技术。它涉及到寻找最接近一组数据点的数学函数的过程。在3D曲线拟合中,该过程被扩展到三维空间,其中的目标是找到最好地表示一组3D数据点的函数。
Python是一种用于科学计算的流行编程语言,它提供了几个可用于3D曲线拟合的库。在本文中,我们将讨论如何使用SciPy库在Python中执行3D曲线拟合。
SciPy库
SciPy库是Python中用于科学计算的强大工具。它为优化、积分、插值和曲线拟合提供了广泛的功能。在本文中,我们将重点介绍该库的曲线拟合功能。
SciPy提供了curve_fit函数,可用于在Python中执行曲线拟合。该函数将待拟合的数据点和待用于拟合的数学函数作为输入。然后,该函数返回最接近输入数据的数学函数的优化参数。
让我们来看看使用Python中的SciPy库对100个随机生成的点进行3D曲线拟合的完整分步过程。
需要安装库:
pip install numpy
pip install scipy
pip install matplotlib
Python中的3D曲线拟合
现在让我们看看如何使用SciPy库在Python中执行3D曲线拟合。我们将首先使用NumPy库生成一些随机的3D数据点。
import numpy as np# Generate random 3D data points
x = np.random.random(100)
y = np.random.random(100)
z = np.sin(x * y) + np.random.normal(0, 0.1, size=100)
data = np.array([x, y, z]).T我们已经在3D空间中生成了100个随机数据点,其中z坐标被定义为具有一些添加的噪声的x和y坐标的函数。
接下来,我们将定义用于曲线拟合的数学函数。在这个例子中,我们将使用一个简单的3次多项式函数。
def func(xy, a, b, c, d, e, f):x, y = xyreturn a + b*x + c*y + d*x**2 + e*y**2 + f*x*y该函数将数据点的x和y坐标以及六个参数a、b、c、d、e和f作为输入。这些参数是在曲线拟合期间将被优化的多项式函数的系数。
我们现在可以使用SciPy库中的curve_fit函数执行曲线拟合。
from scipy.optimize import curve_fit# Perform curve fitting
popt, pcov = curve_fit(func, (x, y), z)# Print optimized parameters
print(popt)输出
[ 0.04416919 -0.12960835 -0.11930051 0.16187097 0.1731539 0.85682108]curve_fit函数将用于曲线拟合的数学函数和要拟合的数据点作为输入。它返回两个数组,popt和pcov。popt数组包含数学函数的参数的优化值,pcov数组包含参数的协方差矩阵。
Python中的curve_fit()函数用于执行非线性回归曲线拟合。它使用最小二乘优化方法来找到最适合给定数据集的用户定义函数的优化参数。
关于popt和pcov
popt和pcov是Python中curve_fit()函数的两个输出。popt是拟合函数的优化参数的1-D阵列,而pcov是优化参数的估计协方差矩阵。
通过使用最小二乘优化算法最小化拟合函数和实际数据点之间的残差平方和来计算Popt。curve_fit()函数使用Levenberg-Marquardt算法来执行此优化。该算法迭代地调整参数值,以最小化目标函数,直到收敛。
使用优化参数值处的目标函数的梯度的协方差矩阵来估计pcov。pcov的对角元素表示优化参数的方差,非对角元素表示参数之间的协方差。pcov用于估计优化参数值的不确定性。
我们现在可以使用优化的参数在3D空间中绘制拟合曲线。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# Create 3D plot of the data points and the fitted curve
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue')
x_range = np.linspace(0, 1, 50)
y_range = np.linspace(0, 1,
X, Y = np.meshgrid(x_range, y_range)
Z = func(X, Y, *popt)
ax.plot_surface(X, Y, Z, color='red', alpha=0.5)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()输出
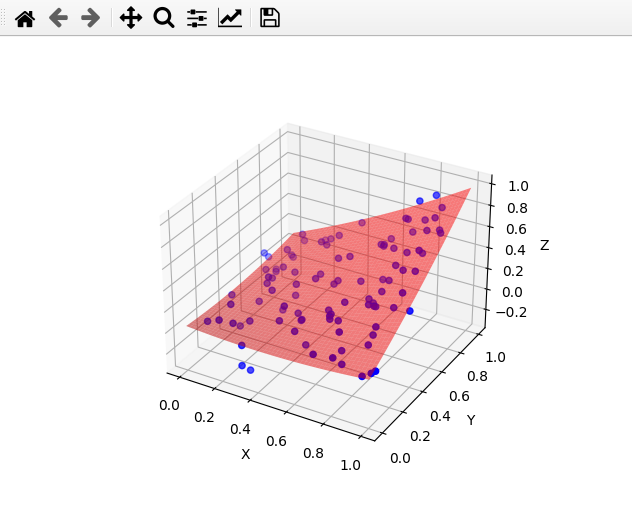
上面的代码创建了数据点和拟合曲线的3D图。蓝点表示原始数据点,红色表面表示拟合曲线。
完整代码:
现在,下面是完整的代码,展示了我们如何使用SciPy库在Python中进行3D曲线拟合。
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# Generate random 3D data points
x = np.random.random(100)
y = np.random.random(100)
z = np.sin(x * y) + np.random.normal(0, 0.1, size=100)
data = np.array([x, y, z]).T# Define mathematical function for curve fitting
def func(xy, a, b, c, d, e, f):x, y = xyreturn a + b*x + c*y + d*x**2 + e*y**2 + f*x*y# Perform curve fitting
popt, pcov = curve_fit(func, (x, y), z)# Print optimized parameters
print(popt)# Create 3D plot of the data points and the fitted curve
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue')
x_range = np.linspace(0, 1, 50)
y_range = np.linspace(0, 1, 50)
X, Y = np.meshgrid(x_range, y_range)
Z = func((X, Y), *popt)
ax.plot_surface(X, Y, Z, color='red', alpha=0.5)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()输出

样条插值
样条插值是一种使用分段多项式函数拟合一组数据点的插值方法。插值函数是通过将数据划分为更小的子集或“段”,并将低次多项式拟合到每个段来构造的。然后,这些多项式段在称为节点的点处连接在一起,形成连续且平滑的插值。
scipy库提供了几个样条插值函数,例如interp2d和Rbf。
import numpy as np
from scipy.interpolate import Rbf
import matplotlib.pyplot as plt# Generate random 3D data points
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = np.cos(np.sqrt(X**2 + Y**2))
# Fit a radial basis function model
rbf = Rbf(X, Y, Z, function="quintic")
Z_pred = rbf(X, Y)# Plot the original data and the fitted function
fig = plt.figure()
ax = fig.add_subplot(projection="3d")
ax.plot_surface(X, Y, Z)
ax.plot_surface(X, Y, Z_pred)
plt.show()输出
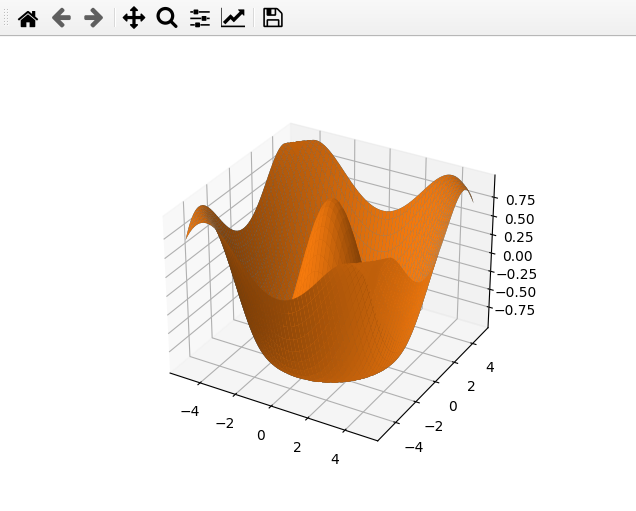
在本文中,我们讨论了如何使用SciPy库在Python中执行3D曲线拟合。我们生成了一些随机的3D数据点,定义了一个多项式函数用于曲线拟合,并使用曲线拟合函数来找到函数的优化参数。然后,我们使用这些参数在3D空间中绘制拟合曲线。
曲线拟合是数据分析和数学建模的强大技术,Python提供了几个库,可以轻松执行曲线拟合。SciPy库是Python中曲线拟合的热门选择,它提供了几个可用于1D,2D和3D空间中曲线拟合的函数。