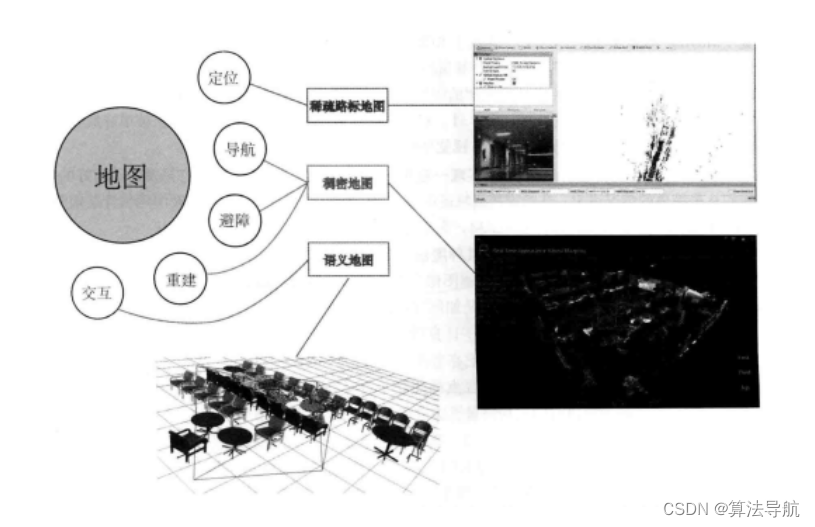
11 建图
11.1 概述
(1)地图的几类用处:
- 定位:
- 导航:机器人在地图中进行路径规划;
- 避障
- 重建
- 交互:人与地图之间的互动
(2)几类地图
- 稀疏地图
- 稠密地图
- 语义地图
11.2 单目稠密重建
11.2.1 立体视觉
(1)稠密重建中,我们需要知道每个像素(或大部分像素)的距离,对此有以下几种方案:
- 使用单目相机,估计相机运动,并且三角化计算像素的距离;
- 使用双目相机,利用左右目的视差计算像素的距离;
- 使用 RGB-D 相机直接获取像素距离。
前两种方式称为立体视觉,在 RGB-D 相机无法很好应用的室外、大型场景中,仍有较好的表现。
11.2.2 极线搜索与块匹配
对于一个单目相机,假设我们观察测到了某个像素 p 1 p_1 p1,显然,还是无法确定它的深度信息,但这个像素对应的空间点应该分布在某条射线上。从另一个视角,这条线的投影也形成了图像平面上的一条线,称为 极线。当知道两个相机之间的运动时,这条极线也是可以确定的。但问题是,极线上的哪个点才是 p 1 p_1 p1 对应的点呢?
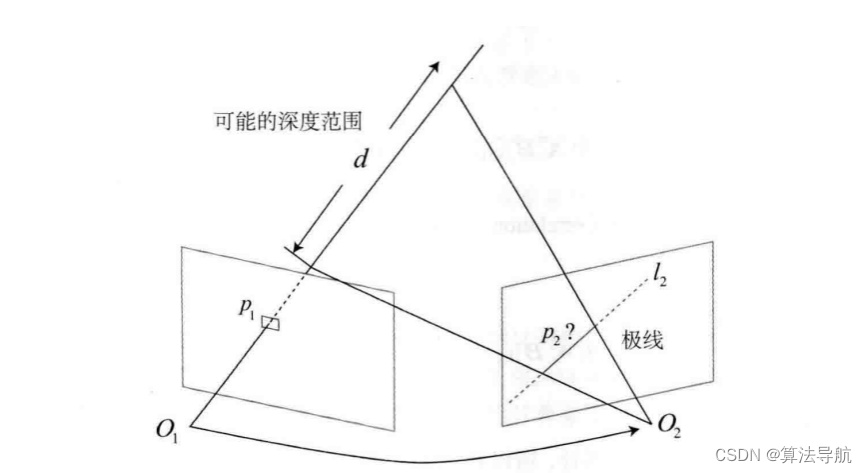
在 p 1 p_1 p1 周围取 w × w w \times w w×w 大小的像素块,在极线上也取相同大小的块,依次进行比较,直至找到 p 2 p_2 p2,这就是所谓的 块匹配。当然这种方法的前提是 图像块灰度不变性,相较于像素灰度不变性,假设更强了。
把 p 1 p_1 p1 周围的像素块记为 A ∈ R w × w \boldsymbol{A} \in \mathbb{R}^{w \times w} A∈Rw×w,把极线上的 n n n 个小块记为 B i , i = 1 , 2 , . . . , n \boldsymbol{B}_i,i=1,2,...,n Bi,i=1,2,...,n,计算二者之间的差异:
- SAD(Sum of Absolute Difference),两个小块的差的绝对值之和:
S ( A , B ) S A D = ∑ i , j ∣ A ( i , j ) − B ( i , j ) ∣ (11-1) S(\boldsymbol{A},\boldsymbol{B})_{\mathrm{SAD}}=\sum_{i,j}|\boldsymbol{A}(i,j)-\boldsymbol{B}(i,j)| \tag{11-1} S(A,B)SAD=i,j∑∣A(i,j)−B(i,j)∣(11-1)
- SSD(Sum of Squared Distance),即平方和:
S ( A , B ) S S D = ∑ i , j ( A ( i , j ) − B ( i , j ) ) 2 (11-2) S(\boldsymbol{A},\boldsymbol{B})_{\mathrm{SSD}}=\sum_{i,j}(\boldsymbol{A}(i,j)-\boldsymbol{B}(i,j))^2 \tag{11-2} S(A,B)SSD=i,j∑(A(i,j)−B(i,j))2(11-2)
- NCC(Normalized Cross Correlation),归一化互相关,计算两个小块的相关性:
S ( A , B ) N C C = ∑ i , j A ( i , j ) B ( i , j ) ∑ i , j A ( i , j ) 2 ∑ i , j B ( i , j ) 2 (11-3) S(\boldsymbol{A}, \boldsymbol{B})_{\mathrm{NCC}}=\frac{\sum_{i, j} \boldsymbol{A}(i, j) \boldsymbol{B}(i, j)}{\sqrt{\sum_{i, j} \boldsymbol{A}(i, j)^{2} \sum_{i, j} \boldsymbol{B}(i, j)^{2}}} \tag{11-3} S(A,B)NCC=∑i,jA(i,j)2∑i,jB(i,j)2∑i,jA(i,j)B(i,j)(11-3)
相关性越接近于 0 表示越不相似,接近 1 表示相似。
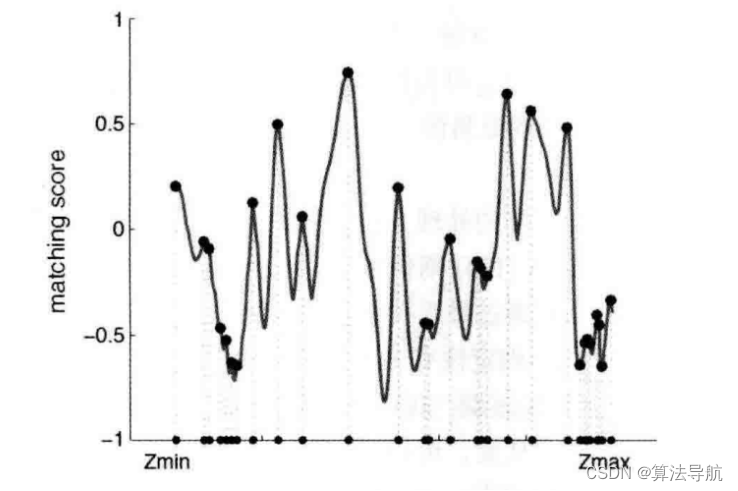
现在,我们在极线上计算了 A \boldsymbol{A} A 与每一个 B i \boldsymbol{B}_i Bi 的相似性度量。这里假设使用 NCC 进行度量,那么,将得到一个沿极线的 NCC分布。我们将使用概率分布描述深度值,而非某个单一数值。于是,问题转化为在不断对不同图像进行极线搜索时,我们估计的深度分布将发生怎样的变化———这就是所谓的 深度滤波器。
11.2.3 高斯分布的深度滤波器
像素点深度的估计,也是一个状态估计问题,于是有滤波器和非线性优化两种方式。但由于 SLAM 实时性要求和算力的限制,一般在建图时采用计算量较小的滤波器进行优化。
假设深度 d d d 符合 高斯分布(也可能是其他分布):
P ( d ) = N ( μ , σ 2 ) (11-4) P(d)=N(\mu, \sigma^2) \tag{11-4} P(d)=N(μ,σ2)(11-4)
每当新的数据到来,我们都会观测它的深度,假设它也符合高斯分布:
P ( d o b s ) = N ( μ o b s , σ o b s 2 ) (11-5) P(d_{\mathrm{obs}})=N(\mu_{\mathrm{obs}}, \sigma_{\mathrm{obs}}^2) \tag{11-5} P(dobs)=N(μobs,σobs2)(11-5)
根据观测到的数据更新原先 d d d 的分布,也就是两个分布相乘,得到融合后的分布 N ( μ f u s e , σ f u s e 2 ) N(\mu_{\mathrm{fuse}}, \sigma_{\mathrm{fuse}}^2) N(μfuse,σfuse2),即
μ fuse = σ o b s 2 μ + σ 2 μ o b s σ 2 + σ o b s 2 , σ fuse 2 = σ 2 σ o b s 2 σ 2 + σ o b s 2 (11-6) \mu_{\text {fuse }}=\frac{\sigma_{\mathrm{obs}}^{2} \mu+\sigma^{2} \mu_{\mathrm{obs}}}{\sigma^{2}+\sigma_{\mathrm{obs}}^{2}}, \quad \sigma_{\text {fuse }}^{2}=\frac{\sigma^{2} \sigma_{\mathrm{obs}}^{2}}{\sigma^{2}+\sigma_{\mathrm{obs}}^{2}} \tag{11-6} μfuse =σ2+σobs2σobs2μ+σ2μobs,σfuse 2=σ2+σobs2σ2σobs2(11-6)
现在关键在于计算 μ o b s \mu_{\mathrm{obs}} μobs 和 σ o b s 2 \sigma_{\mathrm{obs}}^2 σobs2。假设我们找到了 p 1 \boldsymbol{p}_1 p1 对应的点 p 2 \boldsymbol{p}_2 p2,从而观测到了 p 1 \boldsymbol{p}_1 p1 的深度,认为 p 1 \boldsymbol{p}_1 p1 对应的三维点为 P \boldsymbol{P} P。记 O 1 P \boldsymbol{O_1P} O1P 为 p \boldsymbol{p} p, O 1 O 2 \boldsymbol{O_1 O_2} O1O2 为相机平移 t \boldsymbol{t} t, O 2 P \boldsymbol{O_2P} O2P 为 a \boldsymbol{a} a,两个夹角分别为 α \alpha α、 β \beta β。现在考虑极线 l 2 l_2 l2 上存在一个像素大小的误差,使点 p 2 \boldsymbol{p}_2 p2 变为 p 2 ′ \boldsymbol{p}_2' p2′,使 β \beta β 角变为 β ′ \beta ' β′。我们要考虑的是,这个像素误差会导致距离 p \boldsymbol{p} p 和 p ′ \boldsymbol{p'} p′ 产生多大差距。
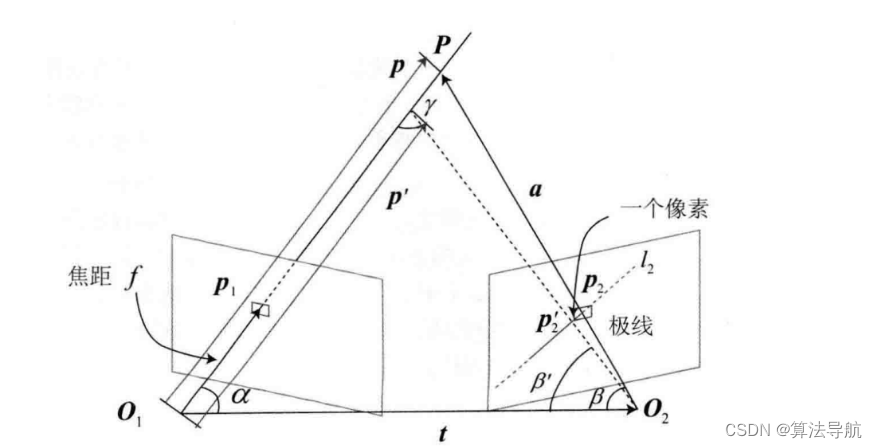
根据几何关系,
a = p − t \boldsymbol{a}=\boldsymbol{p}-\boldsymbol{t} a=p−t
α = arccos ⟨ p , t ⟩ \alpha=\arccos \langle\boldsymbol{p}, \boldsymbol{t}\rangle α=arccos⟨p,t⟩
β = arccos ⟨ a , − t ⟩ (11-7) \beta=\arccos \langle\boldsymbol{a}, \boldsymbol{-t}\rangle \tag{11-7} β=arccos⟨a,−t⟩(11-7)
对 p 2 \boldsymbol{p}_2 p2 扰动一个像素,使 β \beta β 变为 β ′ \beta ' β′,根据几何关系
β ′ = arccos ⟨ O 2 p 2 ′ , − t ⟩ \beta'=\arccos \langle\boldsymbol{O_2p_2'}, \boldsymbol{-t}\rangle β′=arccos⟨O2p2′,−t⟩
γ = π − α − β ′ (11-8) \gamma=\pi-\alpha-\beta' \tag{11-8} γ=π−α−β′(11-8)
由正弦定理
∥ p ′ ∥ = ∥ t ∥ sin β ′ sin γ (11-9) \|\boldsymbol{p'}\|=\|\boldsymbol{t}\| \frac{\sin\beta'}{\sin \gamma} \tag{11-9} ∥p′∥=∥t∥sinγsinβ′(11-9)
这样,我们就确定了由单个像素的不确定引起的深度不确定性,如果认为极线搜索的块匹配仅有一个像素的误差,那么可以设
σ o b s = ∥ p ∥ − ∥ p ′ ∥ (11-10) \sigma_{\mathrm{obs}}=\|\boldsymbol{p}\|-\|\boldsymbol{p'}\| \tag{11-10} σobs=∥p∥−∥p′∥(11-10)
当极线搜索的不确定性大于一个像素时,可按此推导放大这个不确定性。当不确定性小于某个阈值时,就可认为深度数据收敛。
因此,估计稠密深度的完整过程为:
① 假设所有的像素深度都满足某个初始的高斯分布;
② 当新数据产生时,通过极线搜索和块匹配确定投影点的位置;
③ 根据几何关系计算三角化后的深度及不确定性;
④ 将当前观测融合进上一次估计中,若收敛则停止,否则返回第二步。
需要注意的是,这里的深度是指 O 1 P O_1P O1P 的长度,而针孔相机的深度是指像素的 z z z 值。
11.3 实践:单目稠密重建
11.4 RGB-D 稠密建图
(1)点云:直接由 RGB-D 图像生成,不需要额外处理。
(2)网格/面片
(3)八叉树地图
(4)TSDF
11.4.1 八叉树地图
点云有几个明显的缺点:一是规模太大,有很多无效信息,占据大量空间;二是无法处理运动的物体。因此提出了一种灵活的、可压缩的、能随时更新的地图形式:八叉树地图(Octo-tree)。
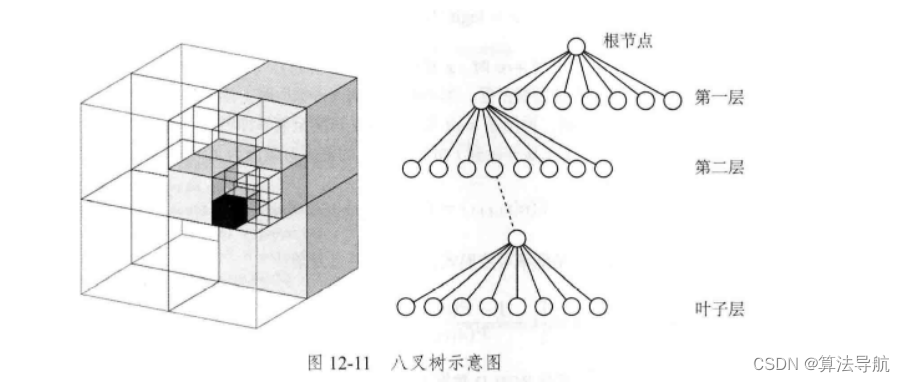
左图显示了一个大立方体不断被均分成八块,直到变为最小的块为止。于是,可以将整个大方块看做根节点,最小的块看做叶子结点,当由下一层节点往上走一层时,地图体积就扩大八倍。当某个方块的所有子节点都被占据或都不被占据时,就没必要展开这个节点,例如地图开始为空白,就只需要一个根节点,而不需要完整的树,所以说八叉树比点云更节省空间。
用概率的形式来表达节点是否被占据,比如初始值为 0.5,如果不断观测到它被占据,则值不断增大;如果不断观测到它是空白,则不断减小。当然,如果这个值不断增大或减小,就可能超出 [ 0 , 1 ] [0,1] [0,1] 之外,因此,我们采用 概率对数值 来描述。设 y ∈ R y\in \mathbb{R} y∈R 为概率对数值, x x x 为 0~1 的概率,定义
y = l o g i t ( x ) = log ( x 1 − x ) (11-11) y=\mathrm{logit}(x)=\log(\frac{x}{1-x}) \tag{11-11} y=logit(x)=log(1−xx)(11-11)
其反变换为:
x = l o g i t − 1 ( y ) = exp ( y ) exp ( y ) + 1 (11-12) x=\mathrm{logit}^{-1}(y)=\frac{\exp(y)}{\exp(y)+1} \tag{11-12} x=logit−1(y)=exp(y)+1exp(y)(11-12)
可以看出,当 y y y 从 − ∞ -\infty −∞ 到 + ∞ +\infty +∞ 时, x x x 范围为 0~1,当 y y y 取 0 时, x x x 取 0.5。因此,不妨用 y y y 来表达节点是否被占据,再将其转换为概率 x x x 即可。假设某节点 n n n,观测数据为 z z z,那么从开始到 t t t 时刻该节点的概率对数值为 L ( n ∣ z 1 : t ) L(n|z_{1:t}) L(n∣z1:t), t + 1 t+1 t+1 时刻为
L ( n ∣ z 1 : t + 1 ) = L ( n ∣ z 1 : t − 1 ) + L ( n ∣ z t ) (11-13) L(n|z_{1:t+1})=L(n|z_{1:t-1})+L(n|z_{t}) \tag{11-13} L(n∣z1:t+1)=L(n∣z1:t−1)+L(n∣zt)(11-13)
将其写成概率形式(也就是 x x x),
P ( n ∣ z 1 : T ) = [ 1 + 1 − P ( n ∣ z T ) P ( n ∣ z T ) 1 − P ( n ∣ z 1 : T − 1 ) P ( n ∣ z 1 : T − 1 ) P ( n ) 1 − P ( n ) ] − 1 (11-14) P\left(n \mid z_{1: T}\right)=\left[1+\frac{1-P\left(n \mid z_{T}\right)}{P\left(n \mid z_{T}\right)} \frac{1-P\left(n \mid z_{1: T-1}\right)}{P\left(n \mid z_{1: T-1}\right)} \frac{P(n)}{1-P(n)}\right]^{-1} \tag{11-14} P(n∣z1:T)=[1+P(n∣zT)1−P(n∣zT)P(n∣z1:T−1)1−P(n∣z1:T−1)1−P(n)P(n)]−1(11-14)
有了对数概率,就可根据 RGB-D 数据更新八叉树地图。假设在 RGB-D 图像中某个像素带有深度 d d d,就说明:在深度值对应的空间点上观察到了一个占据数据,并且,从相机光心出发到这个点的线段上应该是没有物体的(否则被遮挡)。
11.4.2 TSDF 地图和 Fusion 系列
实时三维重建