A - When? A - When?
题目大意
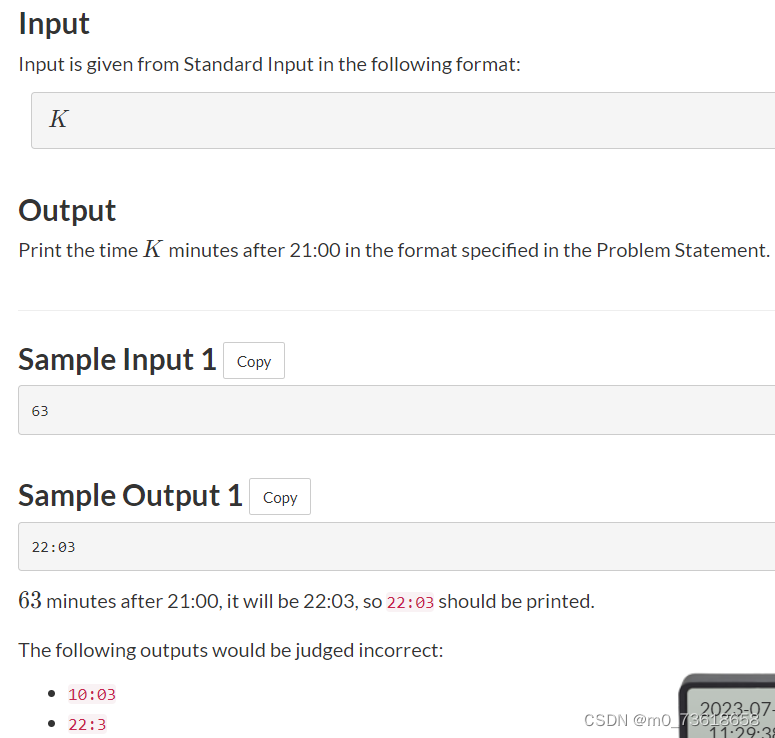
给定一个整数K,表示从日本标准时间21:00开始经过的分钟数。要求将该时间转换为24小时制的时间(HH:MM格式)。
思路分析
可直接分时间打印。关于格式,填充0,打印时间,题解有三种方法:
1.转换成字符,+0
2.规定输出长度,填充0
3.用printf函数指定的数据格式化为字符串并进行输出
时间复杂度
O(1)
代码
1.Defining an original function
#include <iostream>
#include <string>
using namespace std;string fix(int x) {if (x < 10) {return string{'0'} + to_string(x);} else {return to_string(x);}
}int main() {int X;cin >> X;int H = X < 60 ? 21 : 22;int M = X % 60;cout << H << ':' << fix(M) << '\n';
}
2.Using std::setfill and std:::setw
#include <iostream>
#include <iomanip>
using namespace std;int main() {int X;cin >> X;int H = X < 60 ? 21 : 22;int M = X % 60;cout << H << ':' << setw(2) << setfill('0') << M << '\n';return 0;
}
- Using std::printf
#include <iostream>
#include <cstdio>
using namespace std;int main() {int X;cin >> X;int H = X < 60 ? 21 : 22;int M = X % 60;printf("%d:%02d", H, M);return 0;
}
B - Number Box
题目大意
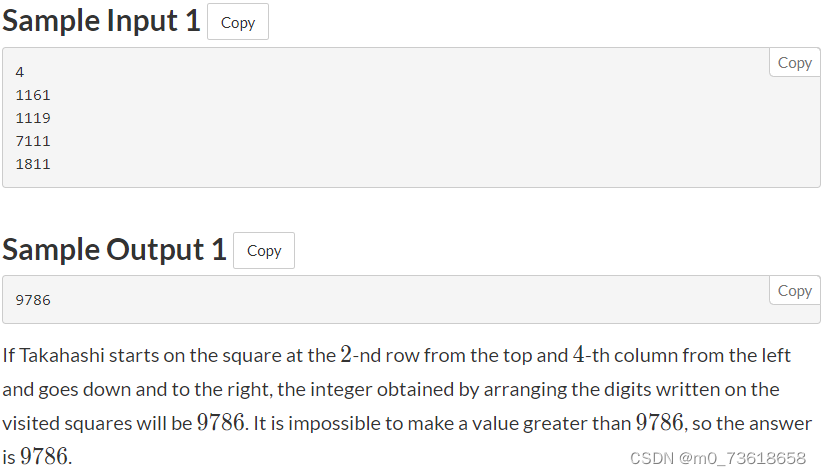
给定一个正整数N和一个N×N的网格,每个方格上都有一个数字。Takahashi从网格中选择一个起始方格,并沿着指定的方向移动N-1次,路径包括起始方格。求所经过方格上数字按访问顺序排列得到的最大整数。
思路分析
穷举法。枚举。
求所有可能路径经过的方格上的数字按访问顺序组成的整数的最大值。由于起点是自由选择的,我们可以枚举所有可能的起点,然后尝试所有八个方向的移动,并计算每条路径对应数字的最大值。
时间复杂度
O(N4)
代码
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {int n;cin>>n;ll ans=0;vector<vector<ll>> a(n,vector<ll>(n));for(int i=0;i<n;i++){for(int j=0;j<n;j++){char c;cin>>c;a[i][j]=c-'0';}}vector<int> p={1,1,1,0,0,-1,-1,-1},q={1,0,-1,1,-1,1,0,-1};for(int i=0;i<n;i++){for(int j=0;j<n;j++){for(int k=0;k<8;k++){ll now=0;ll x=i,y=j;for(int l=0;l<n;l++){now*=10;now+=a[x][y];x+=p[k];y+=q[k];x%=n;x+=n;y%=n;y+=n;x%=n;y%=n;}ans=max(ans,now);}}}cout<<ans<<endl;
}
C - RotationC - Rotation
题目大意
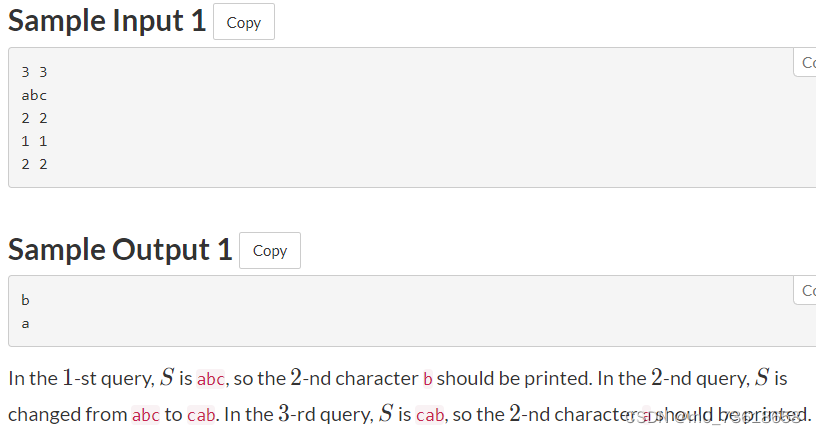
给定一个字符串S和一系列查询操作,其中查询操作有两种类型。第一种类型是将S的最后一个字符删除并添加到开头,第二种类型是打印S中指定位置的字符。需要根据查询操作的要求进行处理并输出结果。
思路分析
注意只知道原字符串的初始位置。找后来的头与原字符串的位置关系。
根据题目要求,对于第一种类型的查询操作,我们需要维护一个变量it,表示当前字符串起始位置(即最后一个字符移动到的位置)。通过取模运算,可以实现将最后一个字符删除并添加到开头的效果。
时间复杂度
O(Q)
代码
#include <bits/stdc++.h>
using namespace std;int main() {int n, q;cin >> n >> q;string s;cin >> s;int it = 0;while (q--) {int op, x;cin >> op >> x;if (op == 1) {it = (it - x + n) % n;} else {x--;cout << s[(it + x) % n] << endl;}}return 0;
}