聚类
问题描述
训练数据: D = { x 1 , x 2 , ⋯ , x m } D=\lbrace x_1,x_2,\cdots,x_m\rbrace D={x1,x2,⋯,xm},其中每个数据为 n n n 维向量 x i = ( x i 1 , x i 2 , ⋯ , x i n ) x_i=(x_{i1},x_{i2},\cdots,x_{in}) xi=(xi1,xi2,⋯,xin);
任务:将 D D D 划分为 k k k 个互不相交的簇。
样本相似性的度量
有序属性的度量
闵可夫斯基距离:
d i s t m k ( x i , x j ) = ( ∑ u = 1 n ∣ x i u − x j u ∣ p ) 1 / p , p ≥ 1 {\rm dist_{mk}}(x_i,x_j)=(\sum\limits_{u=1}^{n}|x_{iu}-x_{ju}|^p)^{1/p},\ p\ge1 distmk(xi,xj)=(u=1∑n∣xiu−xju∣p)1/p, p≥1
余弦相似度:
s i j ( x i , x j ) = x i T x j ∣ ∣ x i ∣ ∣ ⋅ ∣ ∣ x j ∣ ∣ s_{ij}(x_i,x_j)=\frac{x_i^{T}x_j}{||x_i||\cdot ||x_j||} sij(xi,xj)=∣∣xi∣∣⋅∣∣xj∣∣xiTxj
马氏距离:
D M ( x ) = ( x − μ ) T Σ − 1 ( x − μ ) D_M(x)=\sqrt{(x-\mu)^T\Sigma^-1(x-\mu)} DM(x)=(x−μ)TΣ−1(x−μ)
其中 Σ \Sigma Σ 为样本集协方差矩阵。
为啥不用相关系数呢?
无序属性的度量
VDM距离:
V D M p ( a , b ) = ∑ i = 1 k ∣ m u , a , i m u , a − m u , b , i m u , b ∣ p {\rm VDM}_p(a,b)=\sum\limits_{i=1}^{k}|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}|^p VDMp(a,b)=i=1∑k∣mu,amu,a,i−mu,bmu,b,i∣p
其中, m u , a m_{u,a} mu,a 表示在属性 u u u 上取 a a a 的样本数, m u , a , i m_{u,a,i} mu,a,i 表示在 i i i 簇中属性 u u u 上取 a a a 的样本数。
直观上理解,如果两个取值越像,则其在每个簇的差异应该也越小
混合属性的度量
M i n k o V D M p ( x i , x j ) = ( ∑ u = 1 n c ∣ x i u − x j u ∣ p + ∑ u = n c + 1 n V D M p ( x i u , x j u ) ) 1 p {\rm MinkoVDM}_p(x_i,x_j)=(\sum\limits_{u=1}^{n_c}|x_{iu}-x_{ju}|^p+\sum\limits_{u=n_c+1}^{n}{\rm VDM}_p(x_{iu},x_{ju}))^\frac{1}{p} MinkoVDMp(xi,xj)=(u=1∑nc∣xiu−xju∣p+u=nc+1∑nVDMp(xiu,xju))p1
聚类方法
划分聚类——K-Means

关于 K-Means 只适用于“团状”数据的问题,感觉换一种距离度量方式就能解决了吧?
层次聚类
自底向上:先将每个样本看作独立的簇,然后按照相似度进行合并,如 AGNES 算法。
自顶向下:将所有样本看作一个簇,然后逐渐细分,如 DIANA 算法。
密度聚类

DBSCAN 算法:

模型聚类
n n n 维随机变量的高斯分布:
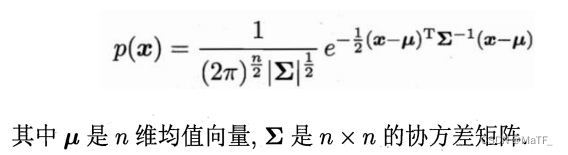
上式可以简记为 p ( x ∣ u , Σ ) p(x|u,\Sigma) p(x∣u,Σ)
高斯混合模型:
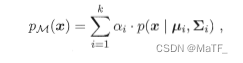
由 k k k 个高斯分布混合而成, α i \alpha_i αi为权重。

关联分析
问题描述
挖掘形如 x → y x\rightarrow y x→y的蕴含式(简单关联:无先后顺序、序列关联:有先后顺序)
支持度:
S u p p o r t ( A ∩ B ) = F r e q ( A ∩ B ) N {\rm Support}(A\cap B)=\frac{{\rm Freq}(A\cap B)}{N} Support(A∩B)=NFreq(A∩B)
置信度:
C o n f i d e n c e = F r e q ( A ∩ B ) F r e q ( A ) {\rm Confidence}=\frac{{{\rm Freq}(A\cap B)}}{{\rm Freq}(A)} Confidence=Freq(A)Freq(A∩B)
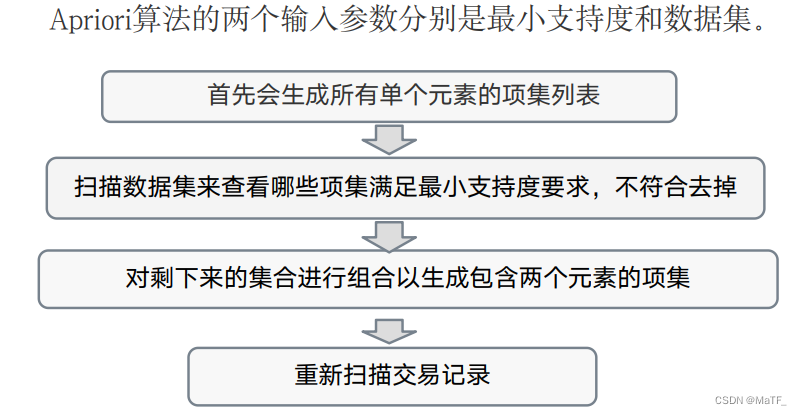
Apriori 算法
如果事件 A 包含 k k k 个元素,则称其为 k k k 项集,若 A 的最小支持度超过阈值,则进一步称其为频繁 k k k 项集。