详解Python中哈希表的使用。站在开发者角度，与大家一起探究哈希的世界。

文章目录

    • 1. 前言
    • 2. 哈希表
      • 2.1 哈希函数
      • 2.2 哈希算法
      • 2.3 常见哈希算法
      • 2.4 哈希冲突
    • 3.总结
      • 关于Python技术储备
        • 一、Python所有方向的学习路线
        • 二、Python基础学习视频
        • 三、精品Python学习书籍
        • 四、Python工具包+项目源码合集
        • ①Python工具包
        • ②Python实战案例
        • ③Python小游戏源码
        • 五、面试资料
        • 六、Python兼职渠道

在这里插入图片描述

1. 前言

哈希表或称为散列表，是一种常见的、使用频率非常高的数据存储方案。

哈希表属于抽象数据结构，需要开发者按哈希表数据结构的存储要求进行API定制，对于大部分高级语言而言，都会提供已经实现好的、可直接使用的API，如JAVA中有MAP集合、C++中的MAP容器，Python中的字典……

使用者可以使用API中的方法完成对哈希表的增、删、改、查……一系列操作。

如何学习哈希表？

可以从2个角度开始：

  • 使用者角度：只需要知道哈希表是基于键、值对存储的解决方案，另需要熟悉不同计算机语言提供的基于哈希表数据结构的 API实现，学会使用 API中的方法。
  • 开发者的角度：则需要知道哈希表底层实现原理，以及实现过程中需要解决的各种问题。本文将站在开发者的角度，带着大家一起探究哈希的世界。

2. 哈希表

什么是哈希表？

哈希表是基于键、值对存储的数据结构，底层一般采用的是列表(数组)。

大家都知道，基于列表（数组）的查询速度非常快，时间复杂度是O（1），常量级别的。

列表的底层存储结构是连续的内存区域，只要给定数据在列表（数组）中的位置，就能直接查询到数据。理论上是这么回事，但在实际操作过程，查询数据的时间复杂度却不一定是常量级别的。

如存储下面的学生信息，学生信息包括学生的姓名和学号。在存储学生数据时，如果把学号为0的学生存储在列表0位置，学号为1的学生存储在列表1位置……

这里把学生的学号和列表的索引号进行关联，查询某一个学生时，知道了学生的学号也就知道了学生数据存储在列表中的位置，可以认为查询的时间复杂度为O(1)。

之所以可以达到常量级，是因为这里有信息关联（学生学号关联到数据的存储位置）。

还有一点，学生的学号是公开信息也是常用信息，很容易获取。

但是，不是存储任何数据时，都可以找到与列表位置相关联的信息。比如存储所有的英文单词，不可能为每一个英文单词编号，即使编号了，编号在这里也仅仅是流水号，没有数据含义的数据对于使用者来讲是不友好，谁也无法记住哪个英文单词对应哪个编号。

所以使用列表存储英文单词后需要询时，因没有单词的存储位置。还是需要使用如线性、二分……之类的查询算法，这时的时间复杂度由使用的查询算法的时间复杂度决定。

如果对上述存储在列表的学生信息进行了插入、删除……等操作，改变了数据原来的位置后，因破坏了学号与位置关联信息，再查询时也只能使用其它查询算法，不可能达到常量级。

是否存在一种方案，能最大化地优化数据的存储和查询？

通过上述的分析，可以得出一个结论，要提高查询的速度，得想办法把数据与位置进行关联。而哈希表的核心思想便是如此。

2.1 哈希函数

哈希表引入了关键字概念，关键字可以认为是数据的别名。如上表，可以给每一个学生起一个别名，这个就是关键字。

Tip： 这里的关键字是姓名的拼音缩写，关键字和数据的关联性较强，方便记忆和查询。

有了关键字后，再把关键字映射成列表中的一个有效位置，映射方法就是哈希表中最重要的概念哈希函数。

关键字是一个桥梁，即关联到真正数据又关联到哈希表中的位置。

关键字也可以是需要保存的数据本身。

哈希函数的功能：提供把关键字映射到列表中的位置算法，是哈希表存储数据的核心所在。如下图，演示数据、哈希函数、哈希表之间的关系，可以说哈希函数是数据进入哈希表的入口。

数据最终会存储在列表中的哪一个位置，完全由哈希算法决定。

当需要查询学生数据时，同样需要调用哈希函数对关键字进行换算，计算出数据在列表中的位置后就能很容易查询到数据。

如果忽视哈希函数的时间复杂度，基于哈希表的数据存储和查询时间复杂度是 O(1)。

如此说来哈希函数算法设计的优劣是影响哈希表性能的关键所在。

2.2 哈希算法

哈希算法决定了数据的最终存储位置，不同的哈希算法设计方案，也关乎哈希表的整体性能，所以，哈希算法就变得的尤为重要。

下文将介绍并纵横比较几种常见的 哈希算法的设计方案。

**Tip：**无论使用何种哈希算法，都有一个根本，哈希后的结果一定是一个数字，表示列表（哈希表）中的一个有效位置。也称为哈希值。

使用哈希表存储数据时，关键字可以是数字类型也可以是非数字类型，其实，关键字可以是任何一种类型。这里先讨论当关键字为非数字类型时设计哈希算法的基本思路。

如前所述，已经为每一个学生提供了一个以姓名的拼音缩写的关键字。

现在如何把关键字映射到列表的一个有效位置？

这里可以简单地把拼音看成英文中的字母，先分别计算每一个字母在字母表中的位置，然后相加，得到的一个数字。

使用上面的哈希思想对每一个学生的关键字进行哈希：

  • zjl的哈希值为 26+10+12=48。
  • llj的哈希值为 12+12+10=34。
  • cl 的哈希值为 3+12=15。
  • zxy的哈希值为 26+25+24=75。

前文说过哈希值是表示数据在列表中的存储位置，现在假设一种理想化状态，学生的姓名都是3个汉字，意味着关键字也是3个字母，采用上面的的哈希算法，最大的哈希值应该是zzz=26+26+26=78，意味着至少应该提供一个长度为78的列表 。

如果，现在仅仅只保存4名学生，虽然只有4名学生，因无法保证学生的关键字不出现zzz，所以列表长度还是需要78。如下图所示。

采用这种哈希算法会导致列表的空间浪费严重，最直观想法是对哈希值再做约束，如除以4再取余数，把哈希值限制在4之内，4个数据对应4个哈希值。我们称这种取余数方案为取余数算法。

取余数法中，被除数一般选择小于哈希表长度的素数。本文介绍其它哈希算法时，也会使用取余数法对哈希值进行适当范围的收缩。

重新对 4 名学生的关键字进行哈希。

  • zjl的哈希值为 26+10+12=48，48 除以 4 取余数，结果是0。
  • llj的哈希值为 12+12+10=34，34 除以 4 取余数，结果是2。
  • cl 的哈希值为 3+12=15，15 除以 4 取余数，结果是3。
  • zzz的哈希值为 26+26+26=78，78 除以 4 取余数，结果是2。

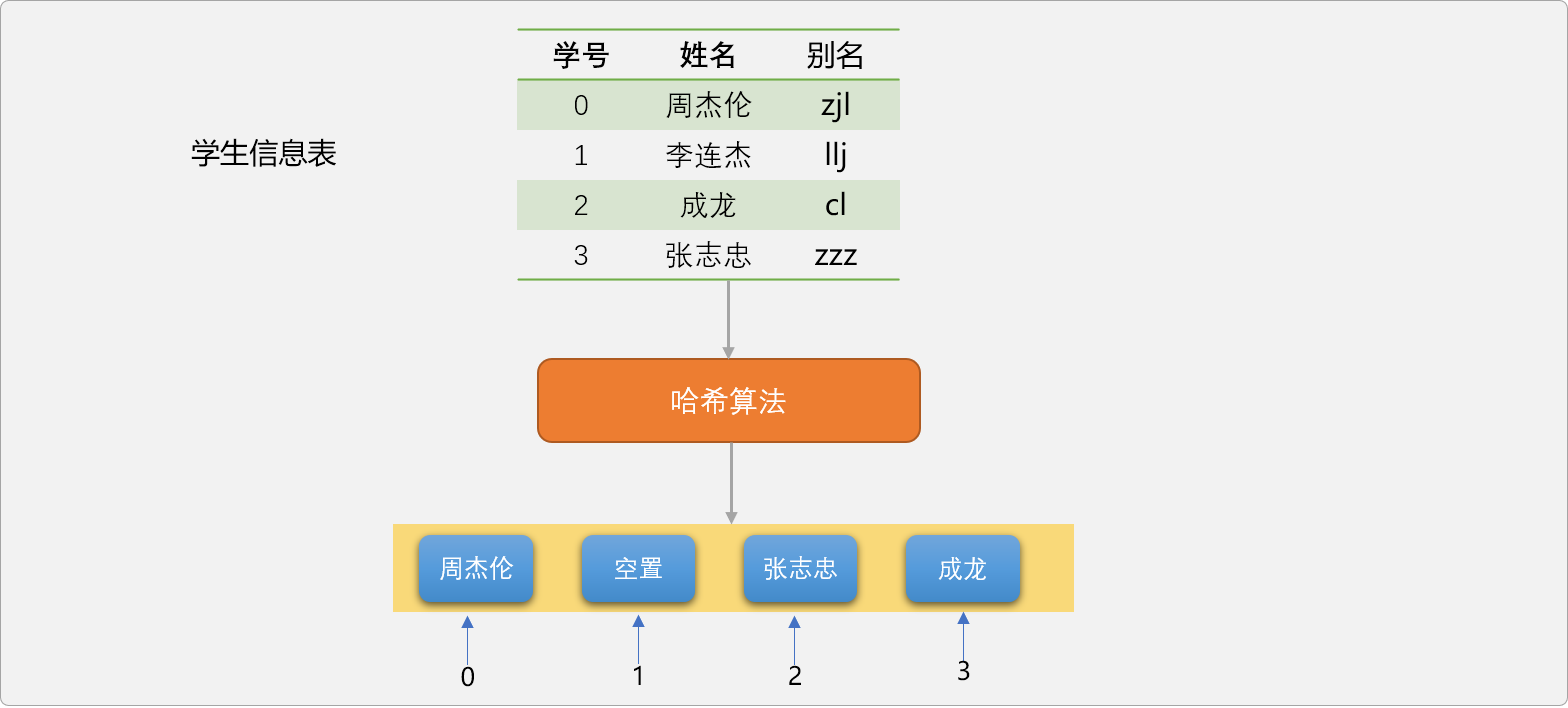
演示图上出现了一个很奇怪的现象，没有看到李连杰的存储信息。

4个存储位置存储4学生，应该是刚刚好，但是，只存储了3名学生。且还有1个位置是空闲的。现在编码验证一下，看是不是人为因素引起的。

'''
哈希函数
'''
def hash\_code(key):# 设置字母 A 的在字母表中的位置是 1pos = 0for i in key:i = i.lower()res = ord(i) - ord('a') + 1pos += resreturn pos % 4

测试代码：

\# 哈希表
hash\_table = \[None\] \* 4
# 计算关键字的哈希值
idx = hash\_code('zjl')
# 根据关键字换算出来的位置存储数据
hash\_table\[idx\] = '周杰伦'
idx = hash\_code('llj')
hash\_table\[idx\] = '李连杰'
idx = hash\_code('cl')
hash\_table\[idx\] = '成龙'
idx = hash\_code('zzz')
hash\_table\[idx\] = '张志忠'
print('哈希表中的数据：', hash\_table)
'''
输出结果：
哈希表中的数据： \['周杰伦', None, '张志忠', '成龙'\]
'''

执行代码，输出结果，依然还是没有看到李连杰的信息。

原因何在？

这是因为李连杰和张志忠的哈希值都是2 ，导致在存储时，后面存储的数据会覆盖前面存储的数据，这就是哈希中的典型问题，哈希冲突问题。

所谓哈希冲突，指不同的关键字在进行哈希算法后得到相同的哈希值，这意味着，不同关键字所对应的数据会存储在同一个位置，这肯定会发生数据丢失，所以需要提供算法，解决冲突问题。

Tip： 研究哈希表，归根结底，是研究如何计算哈希值以及如何解决哈希值冲突的问题。

针对上面的问题，有一种想当然的冲突解决方案，扩展列表的存储长度，如把列表扩展到长度为8。

直观思维是：扩展列表长度，哈希值的范围会增加，冲突的可能性会降低。

'''
哈希函数
'''
def hash\_code(key):# 设置字母 A 的在字母表中的位置是 1pos = 0for i in key:i = i.lower()res = ord(i) - ord('a') + 1pos += resreturn pos % 8# 哈希表
hash\_table = \[None\] \* 8# 保存所有学生
idx = hash\_code('zjl')
hash\_table\[idx\] = '周杰伦'
idx = hash\_code('llj')
hash\_table\[idx\] = '李连杰'
idx = hash\_code('cl')
hash\_table\[idx\] = '成龙'
idx = hash\_code('zzz')
hash\_table\[idx\] = '张志忠'
print('哈希表中的数据：', hash\_table)
'''
输出结果：
哈希表中的数据： \['周杰伦', None, '李连杰', None, None, None, '张志忠', '成龙'\]
'''

貌似解决了冲突问题，其实不然，当试着设置列表的长度为6、7、8、9、10时，只有当长度为8时没有发生冲突，这还是在要存储的数据是已知情况下的尝试。

如果数据是动态变化的，显然这种扩展长度的方案绝对不是本质解决冲突的方案。即不能解决冲突，且产生大量空间浪费。

如何解决哈希冲突，会在后文详细介绍，这里还是回到哈希算法上。

综上所述，我们对哈希算法的理想要求是：

  • 为每一个关键字生成一个唯一的哈希值，保证每一个数据都有只属于自己的存储位置。
  • 哈希算法的性能时间复杂度要低。

现实情况是，同时满足这2个条件的哈希算法几乎是不可能有的，面对数据量较多时，哈希冲突是常态。所以，只能是尽可能满足。

因冲突的存在，即使为 100 个数据提供 100 个有效存储空间，还是会有空间闲置。这里把实际使用空间和列表提供的有效空间相除，得到的结果，称之为哈希表的占有率（载荷因子）。

如上述，当列表长度为 4时， 占有率为 3/4=0.75，当列表长度为 8 时，占有率为 4/8=0.5，一般要求占率控制 在0.6~0.9之间。

2.3 常见哈希算法

前面在介绍什么是哈希算法时，提到了取余数法，除此之外，还有几种常见的哈希算法。

2.3.1 折叠法

折叠法：将关键字分割成位数相同的几个部分（最后一部分的位数可以不同）然后取这几部分的叠加和（舍去进位）作为哈希值。

折叠法又分移位叠加和间界叠加。

  • 移位叠加：将分割后的每一部分的最低位对齐，然后相加。
  • 间界叠加：从一端沿分割线来回折叠，然后对齐相加。

因有相加求和计算，折叠法适合数字类型或能转换成数字类型的关键字。假设现在有很多商品订单信息，为了简化问题，订单只包括订单编号和订单金额。

现在使用用哈希表存储订单数据，且以订单编号为关键字，订单金额为值。

订单编号订单金额
20201011400.00
19981112300.00
20221212200

移位叠法换算关键字的思路：

**第一步：**把订单编号20201011按每3位一组分割，分割后的结果：202、010、11。

按2位一组还是3位一组进行分割，可以根据实际情况决定。

第二步： 把分割后的数字相加202+010+11，得到结果：223。再使用取余数法，如果哈希表的长度为10，则除以10后的余数为3。

这里除以10仅是为了简化问题细节，具体操作时，很少选择列表的长度。

**第三步：**对其它的关键字采用相同的处理方案。

关键字哈希值
202010113
199811122
202212126

编码实现保存商品订单信息：

'''
移位叠加哈希算法
'''
def hash\_code(key, hash\_table\_size):# 转换成字符串key\_s = str(key)# 保存求和结果s = 0# 使用切片for i in range(0, len(key\_s), 3):s += int(key\_s\[i:i + 3\])return s % hash\_table\_size# 商品信息
products = \[\[20201011, 400.00\], \[19981112, 300\], \[20221212, 200\]\]
# 哈希表长度
hash\_size = 10
# 哈希表
hash\_table = \[None\] \* hash\_size
# 以哈希表方式进行存储
for p in products:key = hash\_code(p\[0\], hash\_size)hash\_table\[key\] = p\[1\]
# 显示哈希表中的数据
print("哈希表中的数据：",hash\_table)
# 根据订单号进行查询
hash\_val = hash\_code(19981112, hash\_size)
val = hash\_table\[hash\_val\]
print("订单号为{0}的金额为{1}".format(19981112, val))
'''
输出结果
哈希表中的数据： \[None, None, 300, 400.0, None, None, 200, None, None, None\]
订单号为19981112的金额为300
'''

间界叠加法：

间界叠加法，会间隔地把要相加的数字进行反转。

如订单编号19981112 按3位一组分割，分割后的结果：199、811、12，间界叠加操作求和表达式为199+118+12=339，再把结果339%10=9。

编码实现间界叠加算法：

'''
间界叠加哈希算法
'''
def hash\_code(key, hash\_table\_size):# 转换成字符串key\_s = str(key)# 保存求和结果s = 0# 使用切片for i in range(0, len(key\_s), 3):# 切片tmp\_s = key\_s\[i:i + 3\]# 反转if i % 2 != 0:tmp\_s = tmp\_s\[::-1\]s += int(tmp\_s)return s % hash\_table\_size# 商品信息（数据样例）
products = \[\[20201011, 400.00\], \[19981112, 300\], \[20221212, 200\]\]
# 哈希表长度
hash\_size = 10
# 哈希表
hash\_table = \[None\] \* hash\_size
# 以哈希表方式进行存储
for p in products:key = hash\_code(p\[0\], hash\_size)hash\_table\[key\] = p\[1\]
# 显示哈希表中的数据
print("哈希表中的数据：", hash\_table)
# 根据订单号进行查询
hash\_val = hash\_code(19981112, hash\_size)
val = hash\_table\[hash\_val\]
print("订单号为{0}的金额为{1}".format(19981112, val))
'''
输出结果：
哈希表中的数据： \[None, None, None, 400.0, None, None, 200, None, None, 300\]
订单号为19981112的金额为300
'''

2.3.2 平方取中法

平方取中法：先是对关键字求平方，再在结果中取中间位置的数字。

求平方再取中算法，是一种较常见的哈希算法，从数学公式可知，求平方后得到的中间几位数字与关键字的每一位都有关，取中法能让最后计算出来的哈希值更均匀。

因要对关键字求平方，关键字只能是数字或能转换成数字的类型，至于关键字本身的大小范围限制，要根据使用的计算机语言灵活设置。

如下面的图书数据，图书包括图书编号和图书名称。现在需要使用哈希表保存图书信息，以图书编号为关键字，图书名称为值。

图书编号图书名称
58python 从入门到精通
67C++ STL
78Java 内存模型

使用平方取中法计算关键字的哈希值：

**第一步：**对图书编号58求平方，结果为3364。

第二步：取3364的中间值36，然后再使用取余数方案。如果哈希表的长度为10，则36%10=6。

**第三步：**对其它的关键字采用相同的计算方案。

编码实现平方取中算法：

'''
哈希算法
平方取中
'''
def hash\_code(key, hash\_table\_size):# 求平方res = key \*\* 2#  取中间值，这里取中间 2 位（简化问题）res = int(str(res)\[1:3\])# 取余数return res % hash\_table\_sizehash\_table\_size = 10
hash\_table = \[None\]\*hash\_table\_size
# 图书信息
books = \[\[58, "python 从入门到精通"\], \[67, "C++ STL"\], \[78, "Java 内存模型"\]\]
for b in books:hash\_val = hash\_code(b\[0\],hash\_table\_size)hash\_table\[hash\_val\]=b\[1\]# 显示哈希表中的数据
print("哈希表中的数据：", hash\_table)
# 根据编号进行查询
hash\_val = hash\_code(67, hash\_table\_size)
val = hash\_table\[hash\_val\]
print("编号为{0}的书名为{1}".format(67, val))

上述求平方取中间值的算法仅针对于本文提供的图书数据，如果需要算法具有通用性，则需要根据实际情况修改。

不要被 取中的中字所迷惑，不一定是绝对中间位置的数字。

2.3.3 直接地址法

直接地址法：提供一个与关键字相关联的线性函数。如针对上述图书数据，可以提供线性函数f(k)=2*key+10。

系数2和常数10的选择会影响最终生成的哈希值的大小。可以根据哈希表的大小和操作的数据含义自行选择。

key为图书编号。当关键字不相同时，使用线性函数得到的值也是唯一的，所以，不会产生哈希冲突，但是会要求哈希表的存储长度比实际数据要大。

这种算法在实际应用中并不多见。

实际应用时，具体选择何种哈希算法，完全由开发者定夺，哈希算法的选择没有固定模式可循，虽然上面介绍了几种算法，只是提供一种算法思路。

2.4 哈希冲突

哈希冲突是怎么引起的，前文已经说过。现在聊聊常见的几种哈希冲突解决方案。

2.4.1 线性探测

当发生哈希冲突后，会在冲突位置之后寻找一个可用的空位置。如下图所示，使用取余数哈希算法，保存数据到哈希表中。

哈希表的长度设置为 15，除数设置为 13。

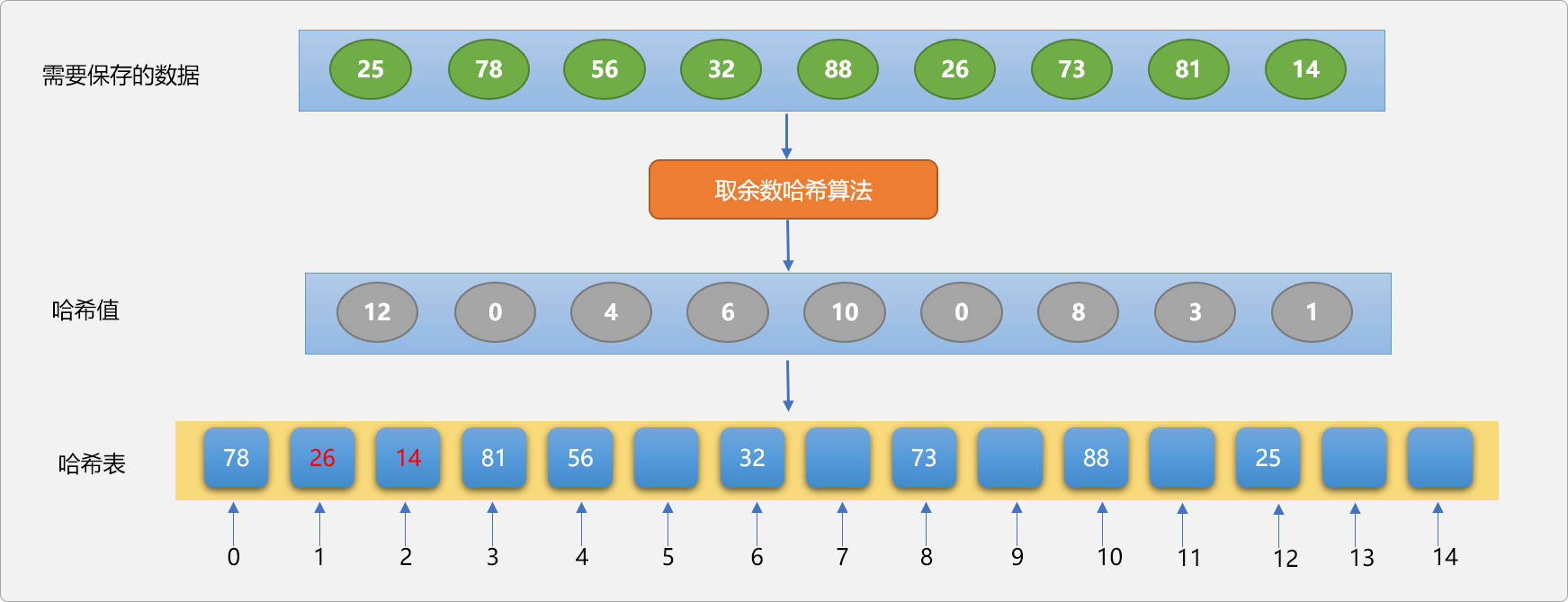
解决冲突的流程：

  • 78和26的哈希值都是 0。而因为78在26的前面，78先占据哈希表的 0位置。
  • 当存储 26时，只能以 0位置为起始位置，向后寻找空位置，因 1位置没有被其它数据占据，最终保存在哈希表的1位置。
  • 当存储数字 14时，通过哈希算法计算，其哈希值是1，本应该要保存在哈希表中1的位置，因1位置已经被26所占据，只能向后寻找空位置，最终落脚在2位置。

线性探测法让发生哈希冲突的数据保存在其它数据的哈希位置，如果冲突的数据较多，则占据的本应该属于其它数据的哈希位置也较多，这种现象称为哈希聚集。

查询流程：

以查询数据14为例。

  • 计算 14的哈希值，得到值为 1 ，根据哈希值在哈希表中找到对应位置。
  • 查看对应位置是否存在数据，如果不存在，宣告查询失败，如果存在，则需要提供数据比较方法。
  • 因 1位置的数据 26并不等于14。于是，继续向后搜索，并逐一比较。
  • 最终可以得到结论14在哈希表的编号为2的位置。

所以，在查询过程中，除了要提供哈希函数，还需要提供数据比较函数。

删除流程：

以删除数字26为例。

按上述的查询流程找到数字26在哈希表中的位置1。

设置位置1为删除状态，一定要标注此位置曾经保存过数据，而不能设置为空状态。为什么？

如果设置为空状态，则在查询数字14时，会产生错误的返回结果，会认为14不存在。为什么？自己想想。

编码实现线性探测法：

添加数据：

'''
线性探测法解决哈希冲突
'''
def hash\_code(key, hash\_table, num):# 哈希表的长度size = len(hash\_table)# 取余数法计算哈希值hash\_val = key % num# 检查此位置是否已经保存其它数据if hash\_table\[hash\_val\] is not None:# 则从hash\_val 之后寻找空位置for i in range(hash\_val + 1, size + hash\_val):if i >= size:i = i % sizeif hash\_table\[i\] is None:hash\_val = ibreakreturn hash\_val# 哈希表
hash\_table = \[None\] \* 15
src\_nums = \[25, 78, 56, 32, 88, 26, 73, 81, 14\]
for n in src\_nums:hash\_val = hash\_code(n, hash\_table, 13)hash\_table\[hash\_val\] = nprint("哈希表中的数据：", hash\_table)
'''
输出结果：
哈希表中的数据： \[78, 26, 14, 81, 56, None, 32, None, 73, None, 88, None, 25, None, None\]
'''

**Tip：**为了保证当哈希值发生冲突后，如果从冲突位置查到哈希表的结束位置还是没有找到空位置，则再从哈希表的起始位置，也就是0位置再搜索到冲突位置。冲突位置是起点也是终点，构建一个查找逻辑环，以保证一定能找到空位置。

for i in range(hash\_val + 1, size + hash\_val):pass

基于线性探测的数据查询过程和存储过程大致相同：

def get(key, hash\_table, num):# 哈希表的长度size = len(hash\_table)# 取余数法计算哈希值hash\_val = key % numis\_exist = False# 检查此位置是否已经保存其它数据if hash\_table\[hash\_val\] is None:# 不存在return Noneif hash\_table\[hash\_val\] != key:# 则从hash\_val 之后寻找空位置for i in range(hash\_val + 1, size + hash\_val):if i >= size:i = i % sizeif hash\_table\[i\] == key:hash\_val = iis\_exist = Truebreakelse:is\_exist=Trueif is\_exist:return hash\_val# 测试   
res = get(25, hash\_table, 13)
print(res)

为了减少数据聚集，可以采用增量线性探测法，所谓增量指当发生哈希冲突后，探测空位置时，使用步长值大于1的方式跳跃式向前查找。目的是让数据分布均匀，减小数据聚集。

除了采用增量探测之外，还可以使用再哈希的方案。也就是提供2个哈希函数，第1次哈希值发生冲突后，再调用第2个哈希函数再哈希，直到冲突不再产生。这种方案会增加计算时间。

2.4.2 链表法

上面所述的冲突解决方案的核心思想是，当冲突发生后，在哈希表中再查找一个有效空位置。

这种方案的优势是不会产生额外的存储空间，但易产生数据聚集，会让数据的存储不均衡，并且会违背初衷，通过关键字计算出来的哈希值并不能准确描述数据正确位置。

链表法应该是所有解决哈希冲突中较完美的方案。所谓链表法，指当发生哈希冲突后，以冲突位置为首结点构建一条链表，以链表方式保存所有发生冲突的数据。如下图所示：

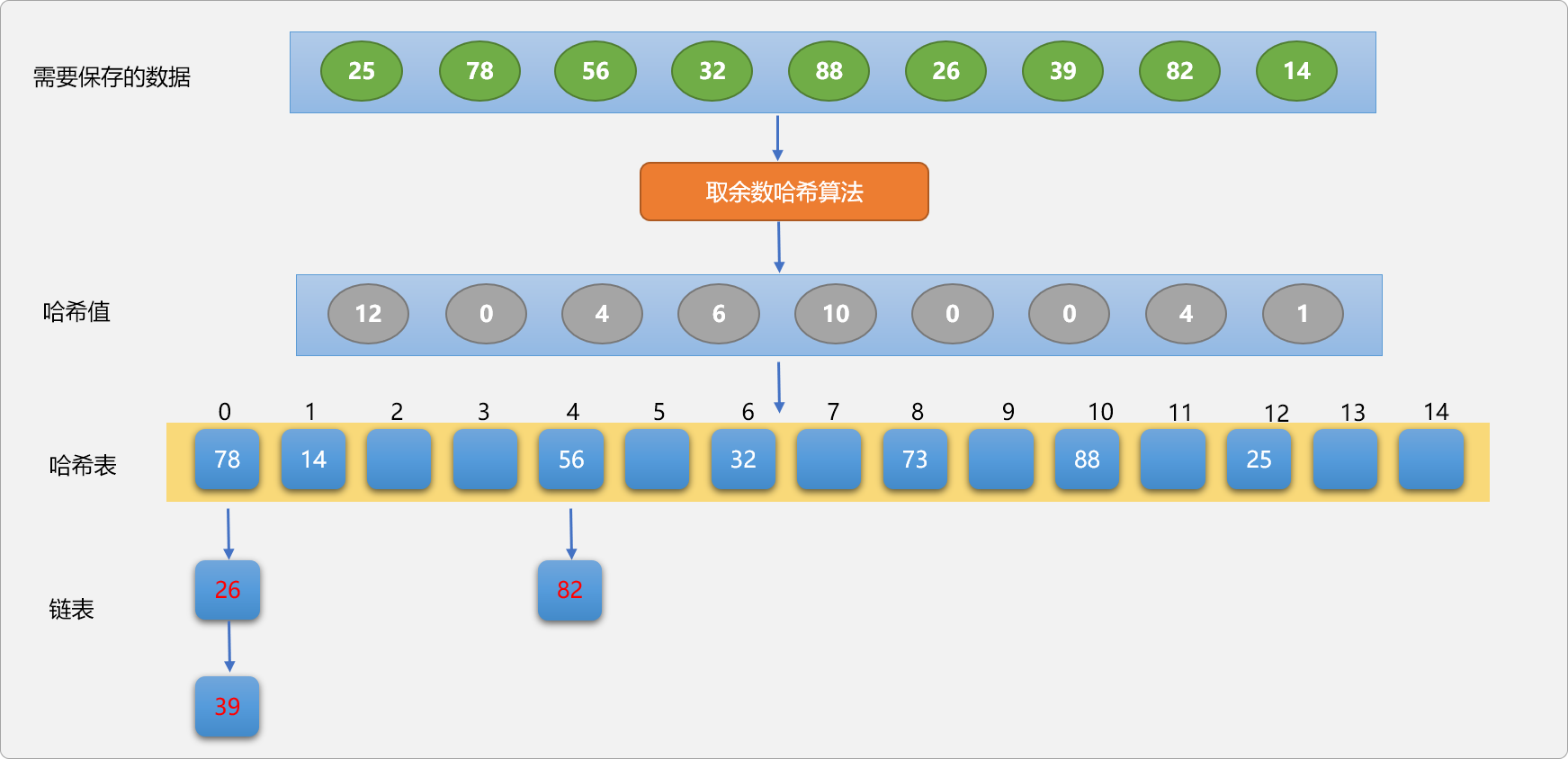
链表方案解决冲突，无论在存储、查询、删除时都不会影响其它数据位置的独立性和唯一性，且因链表的操作速度较快，对于哈希表的整体性能都有较好改善。

使用链表法时，哈希表中保存的是链表的首结点。首结点可以保存数据也可以不保存数据。

编码实现链表法：链表实现需要定义 2 个类，1 个是结点类，1 个是哈希类。

'''
结点类
'''
class HashNode():def \_\_init\_\_(self, value):self.value = valueself.next\_node = None'''
哈希类
'''
class HashTable():def \_\_init\_\_(self):# 哈希表,初始大小为 15，可以根据需要动态修改self.table = \[None\] \* 15# 实际数据大小self.size = 0'''存储数据key:关键字value:值'''def put(self, key, value):hash\_val = self.hash\_code(key)# 新结点new\_node = HashNode(value)if self.table\[hash\_val\] is None:# 本代码采用首结点保存数据方案self.table\[hash\_val\] = new\_nodeself.size+=1else:move = self.table\[hash\_val\]while move.next\_node is not None:move = move.next\_nodemove.next\_node = new\_nodeself.size+=1'''查询数据'''def get(self, key):hash\_val = self.hash\_code(key)if self.table\[hash\_val\] is None:# 数据不存在return -1if self.table\[hash\_val\].value == key:# 首结点就是要找的数据return self.table\[hash\_val\].value# 移动指针move = self.table\[hash\_val\].next\_nodewhile move.value != key and move is not None:move = move.next\_nodeif move is None:return -1else:return move.valuedef hash\_code(self, key):# 这里仅为说明问题，13 的选择是固定的hash\_val = key % 13return hash\_val# 原始数据
src\_nums = \[25, 78, 56, 32, 88, 26, 39, 82, 14\]
# 哈希对象
hash\_table = HashTable()
# 把数据添加到哈希表中
for n in src\_nums:hash\_table.put(n, n)
# 输出哈希表中的首结点数据
for i in hash\_table.table:if i is not None:print(i.value,end=" ")
print("\\n-------------查询-----------")
print(hash\_table.get(26))
'''
输出结果：
78 14 56 32 88 25 
-------------查询-----------
26
'''

3.总结

哈希表是一种高级数据结构，其存储、查询性能非常好，在不考虑哈希哈希算法和哈希冲突的时间复杂度情况下，哈希查找时间复杂度可以达到常量级，成为很多实际应用场景下的首选。

研究哈希表，着重点就是搞清楚哈希算法以及如何解决哈希冲突。在算法的世界时，没有固定的模式，开发者可以根据自己的需要自行设计哈希算法。

关于Python技术储备

学好 Python 不论是就业还是做副业赚钱都不错，但要学会 Python 还是要有一个学习规划。最后大家分享一份全套的 Python 学习资料，给那些想学习 Python 的小伙伴们一点帮助！

微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

一、Python所有方向的学习路线

Python所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照上面的知识点去找对应的学习资源，保证自己学得较为全面。
在这里插入图片描述

二、Python基础学习视频

② 路线对应学习视频

还有很多适合0基础入门的学习视频，有了这些视频，轻轻松松上手Python~在这里插入图片描述
在这里插入图片描述

③练习题

每节视频课后，都有对应的练习题哦，可以检验学习成果哈哈！
在这里插入图片描述
因篇幅有限，仅展示部分资料

三、精品Python学习书籍

当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。
在这里插入图片描述

四、Python工具包+项目源码合集
①Python工具包

学习Python常用的开发软件都在这里了！每个都有详细的安装教程，保证你可以安装成功哦！
在这里插入图片描述

②Python实战案例

光学理论是没用的，要学会跟着一起敲代码，动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。100+实战案例源码等你来拿！
在这里插入图片描述

③Python小游戏源码

如果觉得上面的实战案例有点枯燥，可以试试自己用Python编写小游戏，让你的学习过程中增添一点趣味！
在这里插入图片描述

五、面试资料

我们学习Python必然是为了找到高薪的工作，下面这些面试题是来自阿里、腾讯、字节等一线互联网大厂最新的面试资料，并且有阿里大佬给出了权威的解答，刷完这一套面试资料相信大家都能找到满意的工作。
在这里插入图片描述
在这里插入图片描述

六、Python兼职渠道

而且学会Python以后，还可以在各大兼职平台接单赚钱，各种兼职渠道+兼职注意事项+如何和客户沟通，我都整理成文档了。
在这里插入图片描述
在这里插入图片描述
这份完整版的Python全套学习资料已经上传CSDN，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费】

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/206911.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

ELF header

ELF header

1. ELF header定义 ELF header的定义可以在 /usr/include/elf.h 中找到。Elf32_Ehdr是32位 ELF header的结构体。Elf64_Ehdr是64位ELF header的结构体。 所以，ELF header在ELF文件中的大小与位置是确定的，位置位于文件头部，大小则是Elf_Ehdr…
阅读更多...
​极氪，中国传统汽车品牌电动化的样板间

​极氪，中国传统汽车品牌电动化的样板间

这篇文章早就想写了，因为太忙的原因就一直跳票，正好最近两件事的出现，又触发了想写这篇文章的冲动。 两件事主要是： 一，10 月份各家陆续公布了单月销量以及累计销量； 二，极氪在北京正式发布了 …
阅读更多...
jmeter中调用python代码

jmeter中调用python代码

1、安装pyinstaller pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pyinstaller 2、将py脚本打包 pyinstaller -F venv/get_image/OCR_jmeter_api.py 3、jmeter中添加OS Process Sampler并调用dist下的程序 4、执行jmeter
阅读更多...
【高级网络程序设计】Week2-1 Sockets

【高级网络程序设计】Week2-1 Sockets

一、The Basics 1. Sockets 定义An abstraction of a network interface应用 use the Socket API to create connections to remote computers send data(bytes) receive data(bytes) 2. Java network programming the java network libraryimport java.net.*;similar to…
阅读更多...
网络安全之渗透测试入门准备

网络安全之渗透测试入门准备

渗透测试入门所需知识 操作系统基础：Windows，Linux 网络基础：基础协议与简单原理 编程语言：PHP，python web安全基础 渗透测试入门 渗透测试学习： 1.工具环境准备：①VMware安装及使用&#xff1b…
阅读更多...
OSG文字-HUD显示汉字示例（3）

OSG文字-HUD显示汉字示例（3）

显示文字是一种非常实用的技术&#xff0c;可以用来把一些重要的文字始终显示在屏幕上。HUD的全称是HeadsUpDisplay&#xff0c;即抬头显示&#xff0c;这种技术最早应用在军事战斗机上。 创建HUD显示的基本步骤如下: <1> 创建一个osg::Camera对象&#xff0c;设置视图、…
阅读更多...
苍穹外卖项目笔记（4）——菜品管理

苍穹外卖项目笔记（4）——菜品管理

菜品管理 主要功能模块&#xff1a;新建菜品、修改菜品、启用禁用菜品、菜品的分页查询、删除菜品 代码&#xff1a;GitHub - Echo0701/take-out 1 公共字段自动填充 公共字段指的是业务表中有一些相同的字段&#xff0c;比如创建人、创建时间、修改人、修改时间等&#xff…
阅读更多...
赞！优雅的Python多环境管理神器！易上手易操作！

赞！优雅的Python多环境管理神器！易上手易操作！

前言 Python 的不同版本之间常常存在依赖关系和兼容性问题&#xff0c;为了方便开发人员在 不同项目中使用不同的版本 。 如果大家使用过Python版本管理工具&#xff0c;肯定大多数人使用的都是Anaconda&#xff0c;它是一个优秀的数据科学开发环境&#xff0c;本身也提供了丰…
阅读更多...
有一台电脑一部手机就可以在网上赚钱，这些项目你也可以学会

有一台电脑一部手机就可以在网上赚钱，这些项目你也可以学会

很多人都希望能够在家中或者闲暇的时候&#xff0c;能够在网上赚钱&#xff0c;而网络给了我们这样的可能。只要有一台电脑和一部手机&#xff0c;你就可以开始你的赚钱之旅。这些项目并不难&#xff0c;只要你肯学&#xff0c;就一定能够成功。 1、美工设计 这个副业主要是推荐…
阅读更多...
centos无法进入系统之原因解决办法集合

centos无法进入系统之原因解决办法集合

前言 可爱的小伙伴们&#xff0c;由于精力有限&#xff0c;暂时整理了两类。如果没有你遇到的问题也没有关系&#xff0c;欢迎底下留言评论或私信&#xff0c;小编看到后第一时间帮助解决 一. Centos 7 LVM xfs文件系统修复 情况1&#xff1a; [sda] Assuming drive cache:…
阅读更多...
909-2015-T3

909-2015-T3

文章目录 1.原题2.算法思想2.1.求树的高度2.2.求路径 3.关键代码4.完整代码5.输出结果 1.原题 试编写算法&#xff0c;求给定二叉树上从根节点到叶子节点的一条路径长度等于树的深度减一的路径&#xff08;即列出从根节点到该叶子节点的节点序列&#xff09;&#xff0c;若这样…
阅读更多...
利用QRCode.js生成动态二维码页面

利用QRCode.js生成动态二维码页面

文章目录 QRCode.js简介HTML结构JavaScript生成动态二维码拓展功能1. 联系信息二维码2. Wi-Fi网络信息二维码 总结 &#x1f389;利用QRCode.js生成动态二维码页面 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒&#x1f379;✨博客主页&#xff1a;IT陈寒的博客&#x1f388;该系列文章专栏…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023