题目
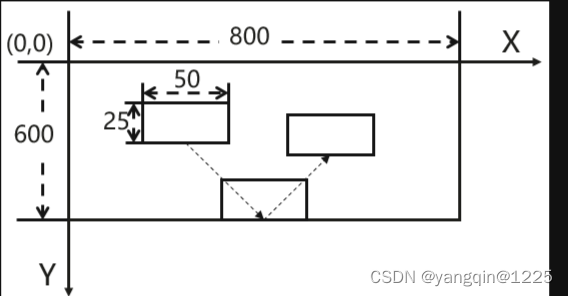
DVD机在视频输出时,为了保护电视显像管,在待机状态会显示"屏保动画”,如下图所示,DVD Logo在屏幕内来回运动,碰到边缘会反弹:请根据如下要求,实现屏保Logo坐标的计算算法
1、屏幕是一个800 * 600像素的矩形,规定屏幕的左上角点坐标原点,沿横边向右方向为X轴,沿竖边向下方向为Y轴
2、Logo是一个50 * 25像素的矩形,初始状态下,左上角点坐标记做(x,y),它在X和Y方向上均以1像素/秒的速度开始运动;
3、遇到屏幕四个边缘后,会发生镜面反弹,即以45°碰撞边缘,再改变方向以45°弹出;当Logo和四个角碰撞时,两个边缘同时反弹的效果是Logo会原路返回。
请编码实现,t秒后Logo左上角点的坐标
输入描述:
输入3个数字,以空格分隔:x y t
第一个数字表示Logo左上角点的初始X坐标
第二个数字表示Logo左上角点的初始Y坐标:
第三个数字表示时间t,题目要求即求t秒后Logo左上角点的位置
输出描述
输出2个数字,以空格分隔:x y
第一个数字表示t秒后,Logo左上角点的X坐标
第二个数字表示t秒后,Logo左上角点的Y坐标
补充说明:
所有用例均保证:
1、输入的x和y坐标会保证整个Logo都在屏幕范围内,Logo不会出画;
2、所有输入数据都是合法的数值,且不会出现负数:
3、t的最大值为100000。
示例1
输入:
0 0 10
输出:
10 10
说明:
输入样例表示Logo初始位置在屏幕的左上角点,10s后,Logo在X和Y方向都移动了10像素,因此输出10 10.
示例2
输入:
500 570 10
输出:
510 570
说明:
输入样例表示初始状态下,Logo的下边缘再有5像素就碰到屏幕下边缘了,5s后,会与屏幕碰撞,碰撞后,斜向45弹出,又经过5s后,Logo与起始位置相比,水平移动了10像素,垂直方向回到了原来的高度。
思路
送分题,两种方法:
- 程序模拟过程,得到t秒后的坐标
- 直接数学计算得出坐标
思路一:程序模拟过程
设一个数组dp=new int[]{1,1},dp[0]=1代表x向右移动1个单位长度,dp[1]代表y向下移动1个单位长度
根据题目要求:
当x到达边界时(x+50=800),此时应该改变移动方向,即dp[0] = -1
同理可得,当y+25=60时,y也应该改变方向,即dp[1] = -1。
什么时候把方向再改回来呢?当x或者y为0时,应该将dp[0]、dp[1]修改为1
写一个循环,直接可以得到t秒后x,y的新坐标。每秒x和y的变化过程为:x=x+dp[0];y=y+d[1]
思路二:数学计算
先不考虑越界情况,(x,y)经过t秒后得到的新坐标应该时(x+t,y+t)
考虑越界情况,x的最大值为750,y的最大值为575。x和y变化规律相同,以x为例说明:
当第一次越界时,比如x计算出来等于800,800%750=50,第一次越界应该向左反弹,所以实际的x为:750-50=700
当第二次越界时,比如x计算出来等于1560,1560%750=10,实际的运动轨迹应该是0-750-0-10,此时x的值就等于10
综上:我们可以直接使用x+t得到x的新坐标,然后计算m,n的值:m=(x+t)/750;n=(x+t)%750
如果m%2=1,即奇数次越界,此时向左反弹,结果应该为750-n;
如果m%2=0,即偶数次越界,此时向右反弹,结果应该为n;
题解
package hwod;import java.util.Arrays;
import java.util.Scanner;public class ScreenProtect {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();int x = nums[0], y = nums[1], t = nums[2];int[] res = screenProtect(x, y, t);for (int i = 0; i < res.length; i++) {if (i != 0) System.out.print(" ");System.out.print(res[i]);}}private static int[] screenProtect(int x, int y, int t) {int width = 800, height = 600;int[] dp = new int[]{1, 1};while (t-- > 0) {if (x == 0) {dp[0] = 1;}if (x +50 == width) {dp[0] = -1;}if (y == 0) {dp[1] = 1;}if (y +25 == height) {dp[1] = -1;}x += dp[0];y += dp[1];}return new int[]{x, y};}private static int[] screenProtect2(int x, int y, int t) {int max_x = 800-50, max_y = 600-25;x = x + t;y = y + t;int modx = x % max_x, mody = y % max_y;x = x / max_x % 2 == 1 ? max_x - modx : modx;y = y / max_y % 2 == 1 ? max_y - mody : mody;return new int[]{x, y};}
}推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。