关键路径问题
名人说:莫听穿林打叶声,何妨吟啸且徐行。—— 苏轼《定风波·莫听穿林打叶声》
本篇笔记整理:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊)
目录
- 关键路径问题
- 〇、概念说明
- 1、AOE网
- 2、关键路径
- 一、问题描述
- 二、问题求解
- ①求事件v最早发生的时间 ve(i)
- ②求事件v最晚发生的时间 vl(i)
- ③求活动a最早开始时间e(i)
- ④求活动a最迟开始时间l(i)
- ⑤求时间余量(d(i))
- ⑥关键活动
- ⑦关键路径
- 三、扩展解法
以下内容,仅供学习交流,且仅在CSDN平台发布,未经授权禁止二次转发。
〇、概念说明
1、AOE网
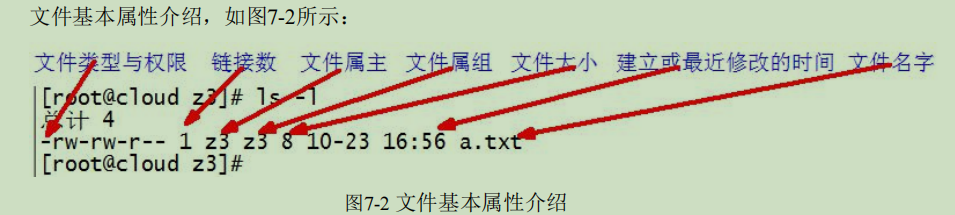
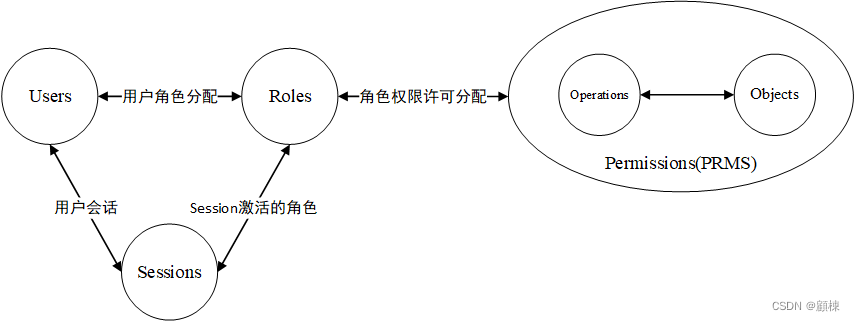
在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称AOE网。
在AOE网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;也仅存在一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
2、关键路径
在AOE网中,有些活动是可以并行进行的。从源点到汇点的有向路径可能有多条,并且这些路径长度可能不同。完成不同路径上的活动所需的时间虽然不同,但是只有所有路径上的活动都已完成,整个工程才能算结束。因此,从源点到汇点的所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动。
(以上概念参考自王道数据结构)
在了解了这些基础概念之后,我们来看一下下面的问题,加深一下理解。
一、问题描述
以2022统考真题为例
【2022统考真题】下面是一个有10个活动的AOE图,时间余量最大的活动是()
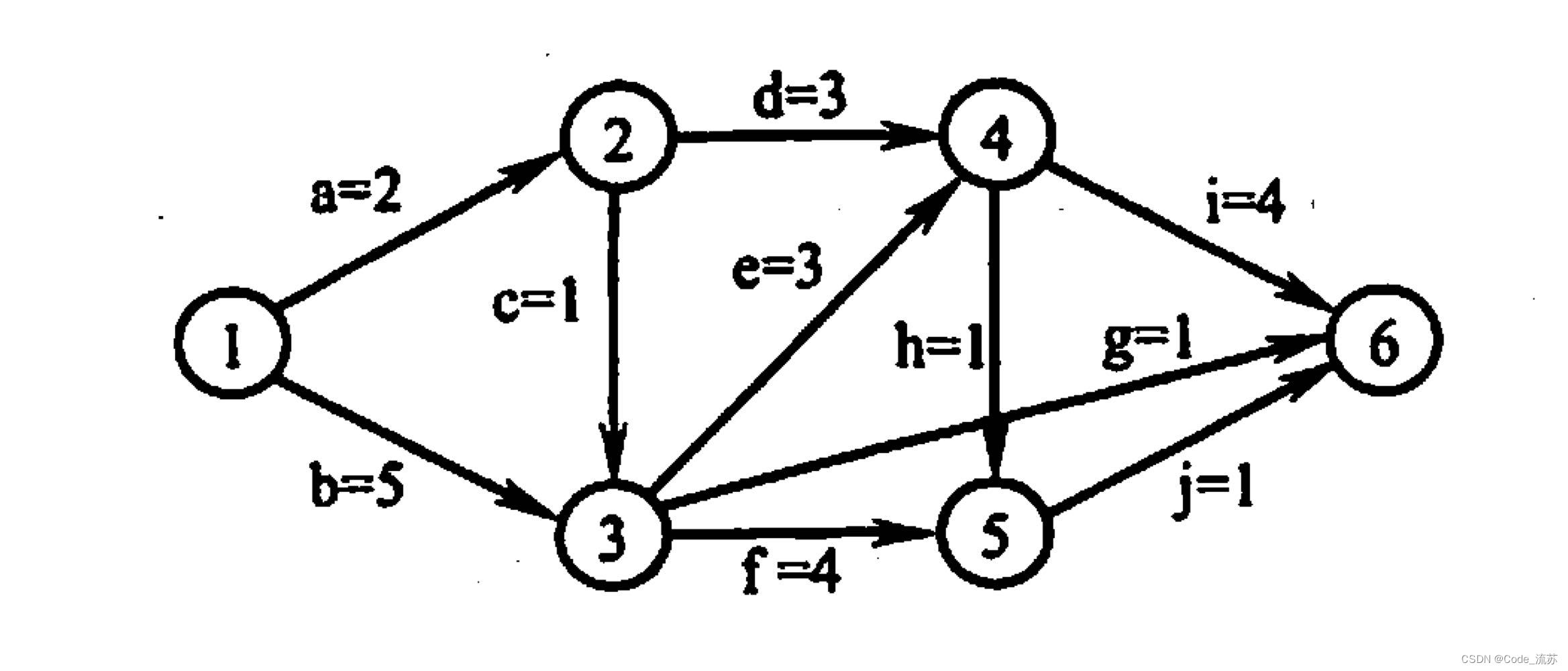
- A.c
- B.g(✔)
- C.h
- D.j
二、问题求解
该类问题的步骤简要来说为以下五步:
- 1️⃣求事件v最早发生的时间 ve(i) 【正向、事件、顶点】
- 2️⃣求事件v最晚发生的时间 vl(i) 【逆向、事件、顶点】
- 3️⃣求活动a最早开始时间e(i) 【正向、活动、有向边】
- 4️⃣求活动a最迟开始时间l(i) 【逆向、活动、有向边】
- 5️⃣求时间余量d(i)【 l(i) - e(i) 】
其中
- 正向表示:从源点到汇点,正向推导
- 逆向表示:从汇点到源点,逆向推导
- 事件表示:v
- 活动表示:a
- 顶点表示:图中各个顶点
- 有向边表示:图中各个箭头有向边
✔ 补充:求时间余量其实就是求4和3的差值(用d(i)来表示),这个差值也就是该活动完成的时间余量。
如果时间余量为0,说明该活动是关键活动,没有缓冲延迟的时间,必须要如期完成。
接下来对以上五个步骤从上到下依次展开计算,具体如下:
①求事件v最早发生的时间 ve(i)
求所有事件的最早发生时间ve[i],按照拓扑排序序列,依次求各个顶点的ve;
设置ve[1]=0,ve[i]=Max {ve[j]+weight(vj,vi)},vj为vi的任意前驱,weight则表示<vj,vi>上的权值。
根据上面的AOE图,可得其拓扑排序序列为:1、2、3、4、5、6。
从源点到汇点顺着来推导事件(顶点)的最早发生事件ve。
ve(1) = 0
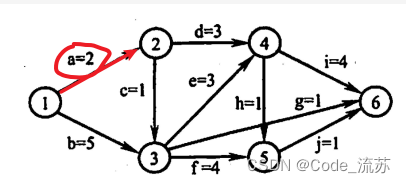
由图可以得出
ve(2) = 0+2 = 1
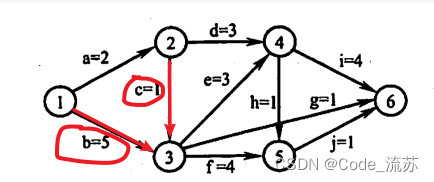
ve(3) = Max{ve(2)+1,ve(1)+5} = Max{3,5} = 5
…
依次类推,可得表格中所示数据:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| ve(i) | 0 | 2 | 5 | 8 | 9 | 12 |
②求事件v最晚发生的时间 vl(i)
求所有事件的最迟发生时间vl[i],按照逆拓扑排序序列,依次求各个顶点的vl;设置vl[汇点]=ve[汇点],vl[i]=Min {vl[j]-weight(vi,vj)},vi为vj的任意前驱。
根据①中所得的拓扑排序,可得逆拓扑排序序列为:6、5、4、3、2、1
从汇点到源点逆着来推导事件(顶点)的最晚发生时间vl。
vl(6) = ve(6) = 12
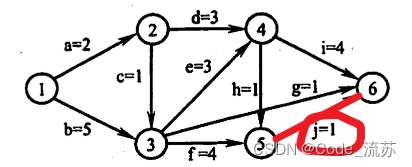
vl(5) = 12 - 1 = 11
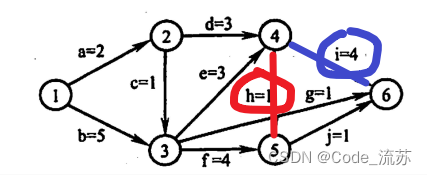
vl(4) = Min {vl(5)-1,vl(6)-4}= Min{10,8} = 8
…
依次类推,最终可得:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| vl(i) | 0 | 4 | 5 | 8 | 11 | 12 |
③求活动a最早开始时间e(i)
求所有活动的最早开始时间e[i],若边<vi,vj>表示活动i,则有e[j]=ve[i]。
从源点到汇点推导活动(有向边)的最早发生时间e。
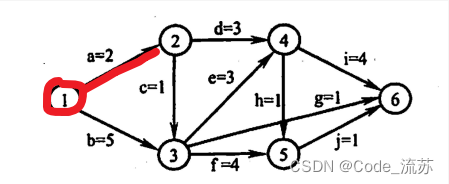
e(a) = ve(1) = 0
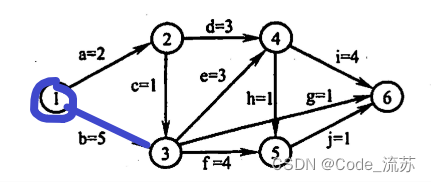
e(b) = ve(1) = 0
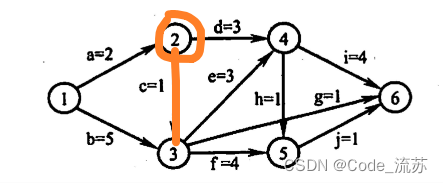
e(c ) = ve(2) = 2
…
依次类推,最终可得:
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| e(i) | 0 | 0 | 2 | 2 | 5 | 5 | 5 | 8 | 8 | 9 |
④求活动a最迟开始时间l(i)
求所有活动的最迟开始时间l,若边<vi,vj>表示活动i,则有l[i]=vl[j]-weight(vi,vj)。
从汇点到源点推导活动(有向边)的最晚发生时间l。
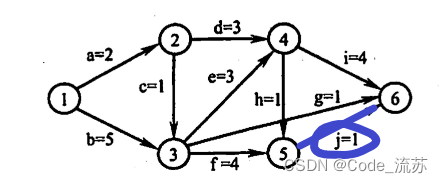
l(j) = vl(6) - 1 = 12 - 1 = 11
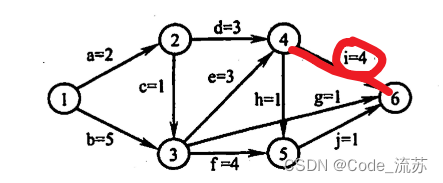
l(i) = vl(6) - 4 = 12 - 8 = 4
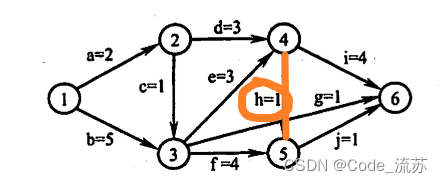
l(h) = vl(5) - 1 = 11 - 1 = 10
…
依次类推,最终可得l的值如下表:
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| l(i) | 2 | 0 | 4 | 5 | 5 | 7 | 11 | 10 | 8 | 11 |
⑤求时间余量(d(i))
最后,让l(i)-e(i)得到d(i)
d(a) = l(a) - e(a) = 2 - 0 = 2
d(b) = l(b) - e(b) = 0 - 0 = 0
…
依次类推,即可得出我们要求的时间余量d:
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| d(i) | 2 | 0 | 2 | 3 | 0 | 2 | 6 | 2 | 0 | 2 |
整体表格如下:
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| e(i) | 0 | 0 | 2 | 2 | 5 | 5 | 5 | 8 | 8 | 9 |
| l(i) | 2 | 0 | 4 | 5 | 5 | 7 | 11 | 10 | 8 | 11 |
| d(i) | 2 | 0 | 2 | 3 | 0 | 2 | 6 | 2 | 0 | 2 |
根据表格中所得,时间余量最大的活动是 g,余量为6。
补充一下关键活动和关键路径,具体内容如下:
⑥关键活动
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| e(i) | 0 | 0 | 2 | 2 | 5 | 5 | 5 | 8 | 8 | 9 |
| l(i) | 2 | 0 | 4 | 5 | 5 | 7 | 11 | 10 | 8 | 11 |
| d(i) | 2 | 0 | 2 | 3 | 0 | 2 | 6 | 2 | 0 | 2 |
根据关键活动的定义,可得关键活动有b、e、i,这些活动都是无法延迟进行的活动,必须如期进行。
⑦关键路径
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| e(i) | 0 | 0 | 2 | 2 | 5 | 5 | 5 | 8 | 8 | 9 |
| l(i) | 2 | 0 | 4 | 5 | 5 | 7 | 11 | 10 | 8 | 11 |
| d(i) | 2 | 0 | 2 | 3 | 0 | 2 | 6 | 2 | 0 | 2 |
根据关键活动,可以画出关键路径如下:
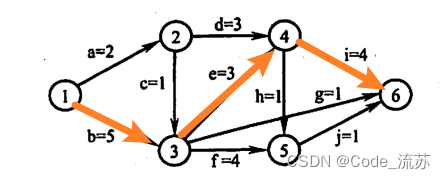
那么问题来了,关于上面时间余量那一块的求解,有没有其它一些简便一些的算法呢?
自然是有的(但方法不能保证百分百正确率,存在一定的技巧性),可以看看以下的一种扩展解法,但是算法思路肯定不止这一种,大家可以集思广益在评论区分享一下!
三、扩展解法
扩展解法思路参考自一位博主写的408真题篇:2022 408真题数据结构篇,个人进行了改善。
可以借助贪心算法的思想来选择。
可以先找出里面最长的几条边构造关键路径,b=5、f=4、i=4、d=3、e=3,枚举到这里就差不多了,我们发现 b=5、e=3、i=4 已经能将起点终点连通了。
假设这就是起点到终点的最长路径,下面开始看看起点到终点的最短路径 a=2、c=1、g=1,我们可以观察到反差最明显的,就是路径3 -> 6 可以分解为3->4->6,g 的时间余量明显是很大的。
但是要注意的是,这种贪心解法高效,但是正确率并非 100%。
- 如果想保证正确率,第一种解法较为妥当;
- 如果追求高效,可以从尝试一下贪心或者其它算法的求解方法。
以上就是本文的全部内容,感谢观看!
Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder)
点赞加关注,文章收藏不迷路!本篇文章对你有帮助的话,还请多多点赞支持!