文章目录
- 题目一
- 分析
- 代码实战
- 题目二
- 分析
- 代码实战
- 补充(快排与归并)
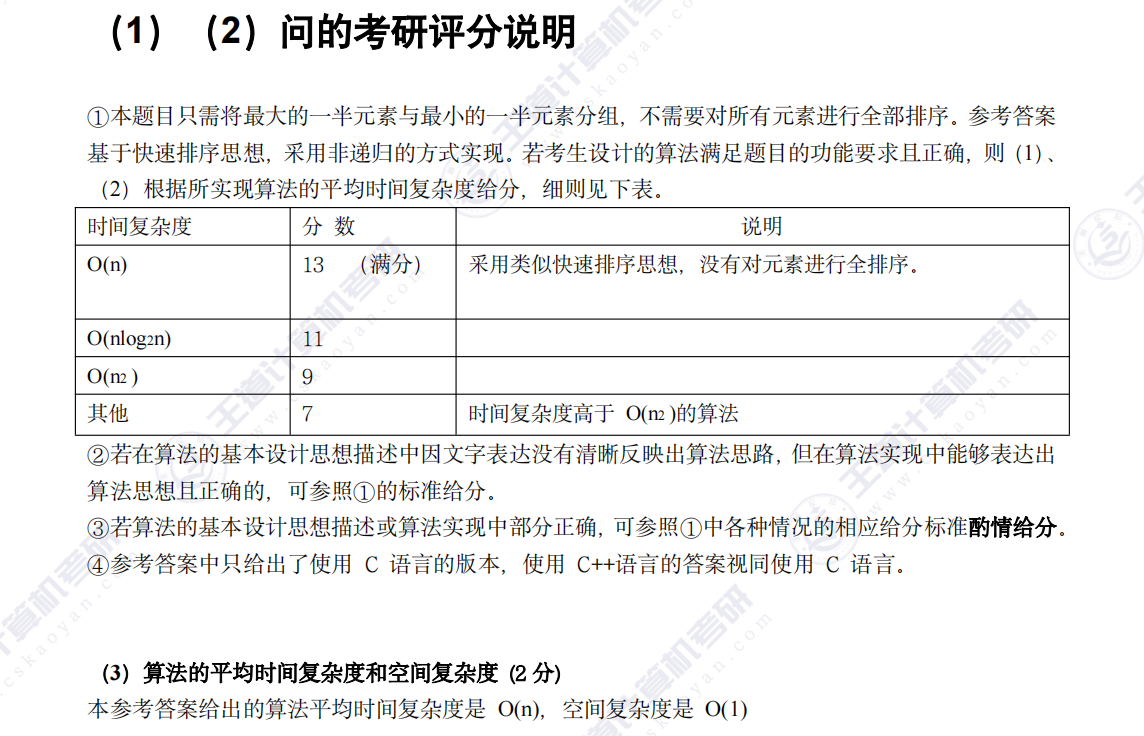
- 数据结构大题注意点!!!(评分标准)
题目一

分析
(1)算法的基本设计思想
由题意知,将最小的nl2个元素放在Ai中,其余的元素放在A2中,分组结果即可满足题目要求。仿照快速排序的思想,基于枢轴将n个整数划分为两个子集。根据划分后枢轴所处的位置i分别处理:
①若i=n/2,则分组完成,算法结束;
②若i<n/2,则枢轴及之前的所有元素均属于Ar,继续对i之后的元素进行划分;③若 i> n/2),则枢轴及之后的所有元素均属于Az,继续对i之前的元素进行划分
(2)间代码实战部分。
(3) 基于该设计思想实现的算法,毋须对全部元素进行全排序,其平均时间复杂度是O(n),空间复杂度是O(1)。
代码实战
实现思想:
- 本题可以用快速排序思想实现,不用考虑将序列排好序然后求|S1-S2|
- 题目首要满足的条件是|n1-n2|最小,然后是|S1-S2|最大这很容易让我们想到
- 将序列分为两个等长的序列这样|n1-n2|=0。并且当小的在一边,大的在一边此时会满足|S1-S2|最大
- 我们可以直接使用快速排序或者堆排序进行排序,将会得到时间复杂度为O(n*(log2^n))的结果。
- 本题中我们不在乎两部分是否有序,我们只在乎找出中位数。并将中位数放在n/2的位置。
- 我们在可以借助快速排序的思想快速实现定位中位数。我们尝试将序列划分为两部分,左边是比
- 分割元素小的,右边是比分割元素大的,会出现以下情况:
- 当分割元素位于n/2位置时,此元素就是我们所要找到值。
- 当分割元素位于n/2左边时,我们将舍弃分割元素及其左边元素,缩小分割
- 有了上面的思路于是我们可以进行以下编码。
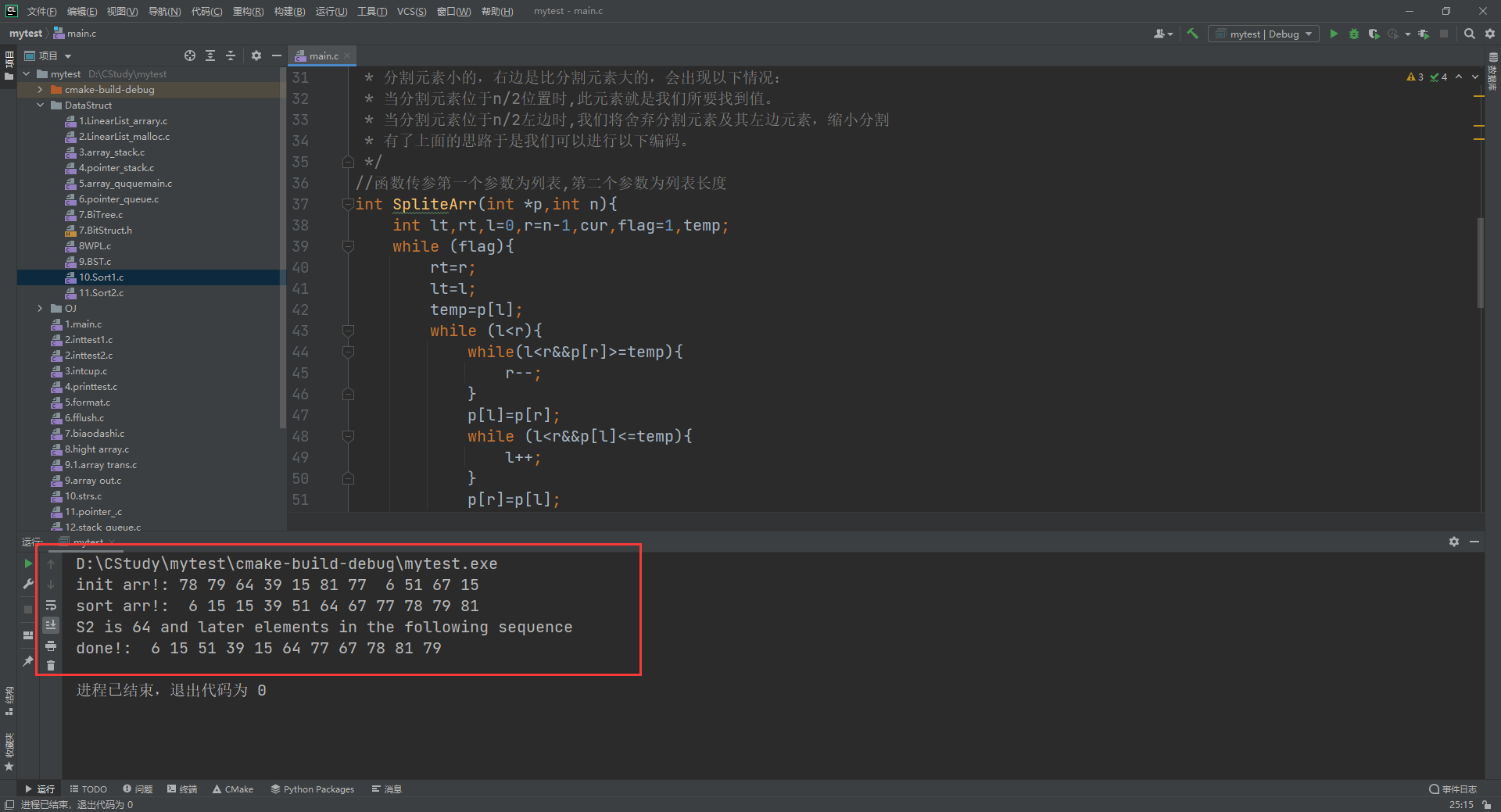
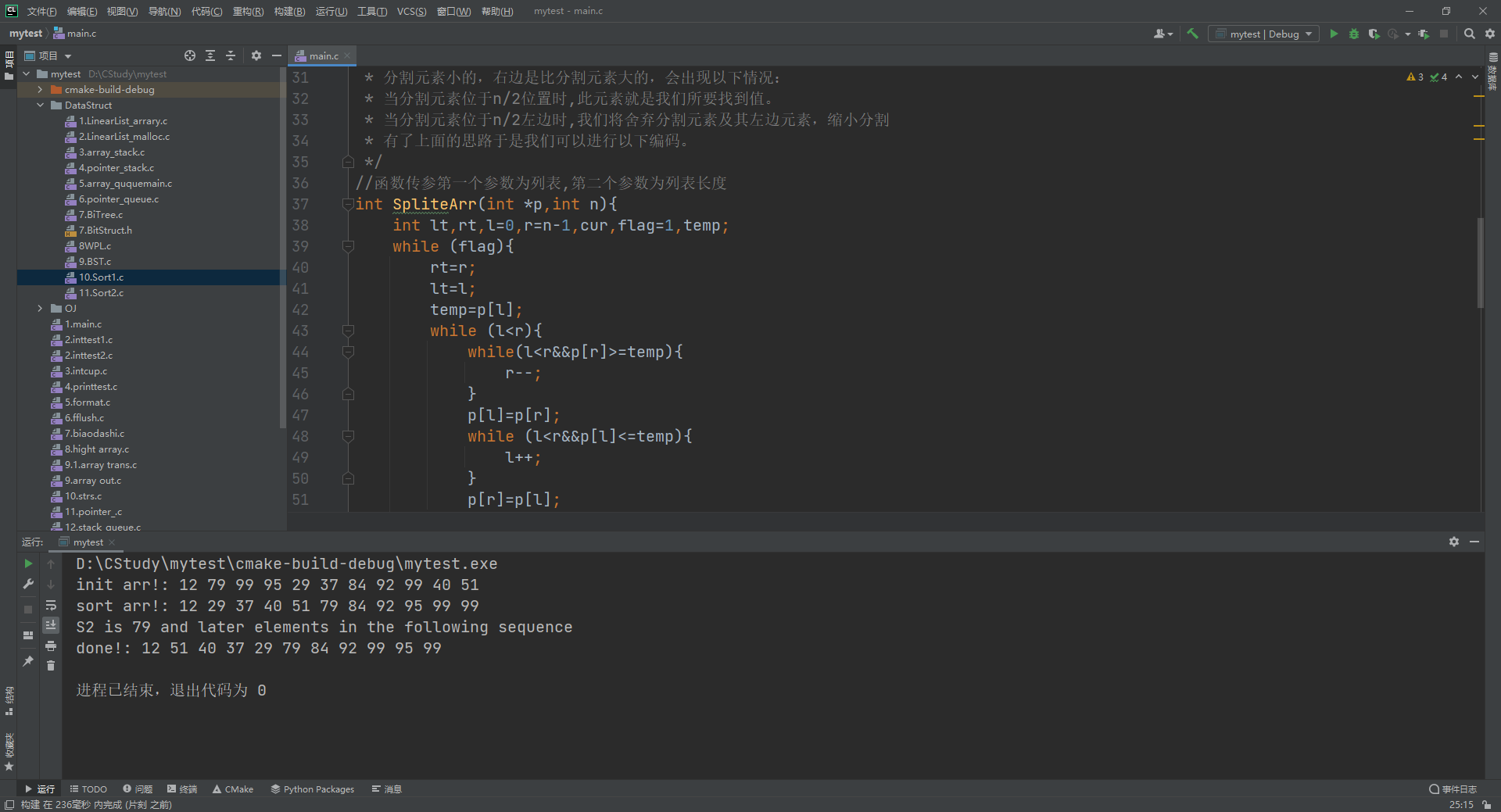
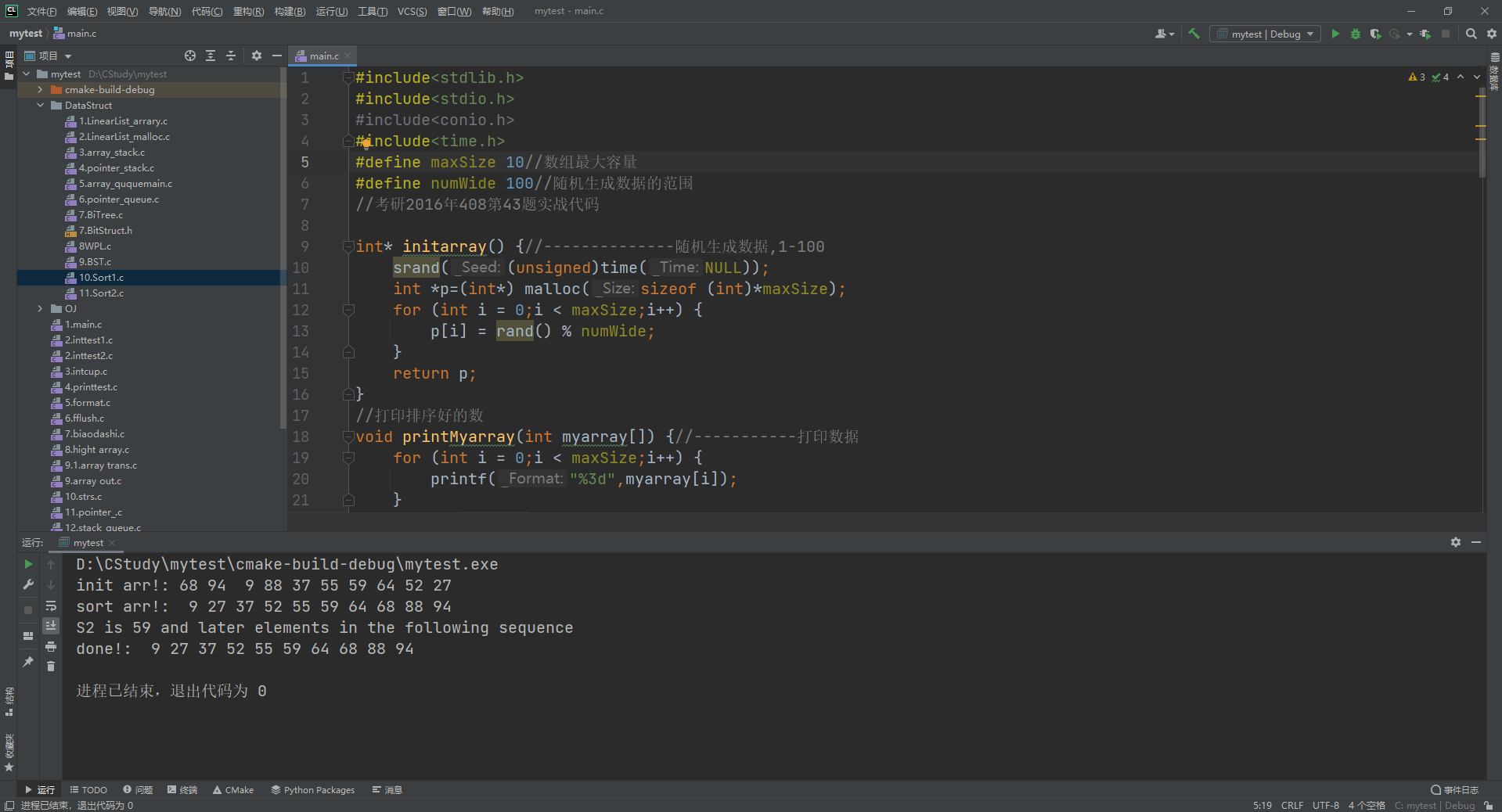
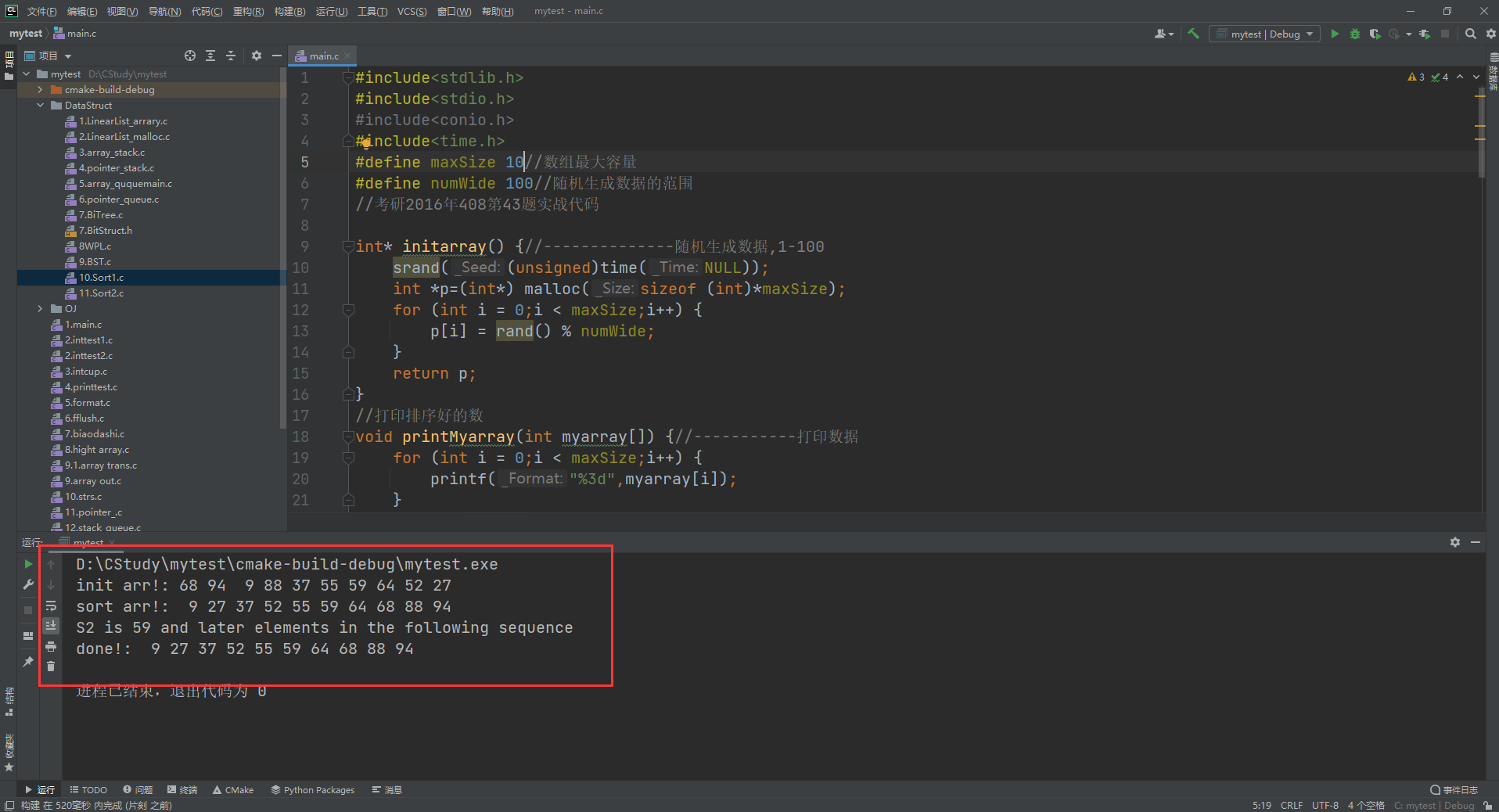
可以从下面图片中可以看出,无论在序列元素个数是奇数还是偶数的情况下结果都是准确的!
注意是先r--还是先l++,为了避免不必要的麻烦一定要按规范写!
#include<stdlib.h>
#include<stdio.h>
#include<conio.h>
#include<time.h>
#define maxSize 11//数组最大容量
#define numWide 100//随机生成数据的范围
//考研2016年408第43题实战代码int* initarray() {//--------------随机生成数据,1-100srand((unsigned)time(NULL));int *p=(int*) malloc(sizeof (int)*maxSize);for (int i = 0;i < maxSize;i++) {p[i] = rand() % numWide;}return p;
}
//打印排序好的数
void printMyarray(int myarray[]) {//-----------打印数据for (int i = 0;i < maxSize;i++) {printf("%3d",myarray[i]);}printf("\n");
}
//函数传参第一个参数为列表,第二个参数为列表长度
int SpliteArr(int *p,int n){int lt,rt,l=0,r=n-1,cur,flag=1,temp;while (flag){rt=r;lt=l;temp=p[l];while (l<r){while(l<r&&p[r]>=temp){r--;}p[l]=p[r];while (l<r&&p[l]<=temp){l++;}p[r]=p[l];}p[l]=temp;cur=l;if(cur>(n-1)/2){r=cur-1;l=lt;}else if(cur<(n-1)/2){l=cur+1;r=rt;}if(cur==(n-1)/2){flag=0;}}return n%2==0?p[cur+1]:p[cur];
}
void SelectSort(int *p){for(int i=0;i<maxSize-1;i++){for(int j=i+1;j<maxSize;j++){if(p[i]>p[j]){int temp=p[i];p[i]=p[j];p[j]=temp;}}}
}int main(){int *p=initarray();printf("init arr!:");printMyarray(p);int *p1=initarray();SelectSort(p1);printf("sort arr!:");printMyarray(p1);printf("S2 is %d and later elements in the following sequence\n",SpliteArr(p,maxSize));printf("done!:");printMyarray(p);return 0;
}
题目二

分析
方法一:最小值(选择排序思想)⑴算法思想(高教社官方答案)
定义含10个元素的数组A,初始时元素值均为该数组类型能表示的最大数MAX。for M中的每个元素s
if (s <A[9])丢弃A[9]并将s按升序插人到A中;(插入排序的算法)当数据全部扫描完毕,数组A[0]~A[9]保存的即是最小的10个数。
2时间复杂度:O(n),每次要插人时都是需要对小数组A进行遍历的空间复杂度:O(1),中间过程额外需要常数个变量。
如果这里将10修改为k,则:
时间复杂度:O(nk),需要遍历k次数组。
空间复杂度:O(1),中间过程额外需要常数个变量。
方法二:堆(堆排序思想)
定义含10个元素的大根堆H,元素值均为该堆元素类型能表示的最大数MAX。for M中的每个元素s
if (s<H的堆顶元素)删除堆顶元素并将s插入到H中;当数据全部扫描完毕,堆H中保存的即是最小的10个数。
2〉算法平均情况下的时间复杂度是O(n),空间复杂度是O(1)。进一步解析:
先用A[0:9]原地建立大顶堆((注意:这里不能用小顶堆),遍历A[10:n],每个元素A[i]逐一和堆顶元素A[0]进行比较,其中11<i<n ,如果A[i]大于等于堆顶元素A[0],不进行任何操作,如果该元素小于堆顶元素A[0],那么就删除堆顶元素,将该元素放入堆顶,即
令A[0]=A[i],然后将A[0:9]重新调整为大顶堆。
最后堆A[0:9]中留存的元素即为最小的10个数。
方法三:(这个高教社没给) 通过快速排序
方法三:(这个高教社没给)
通过快速排序,分割思想,第一次知道n/2位置,再次 partition得到n/4,最终缩小为10个,就拿到了最小的10个元素,遍历的平均次数是n+n/2+n/4+…1,次数为2n,因此时
间复杂度为O(n)。由于我们不进行快排,只是记录剩余部分的起始和结束,因此空间复杂度是O(1)。
代码实战
代码实战。。。。这个题目没有要求代码实战,只要我们的思想是可行的,那么一定可以实现,如果感兴趣的话自己写一份代码吧,我就不瞎搞了。
补充(快排与归并)
偶然间发现快排与归并的实现思想有点类似,于是网上找了一下异同点,总结如下:
归并排序和快排的相同点:
- 1,利用分治思想
- 2,具体实现都用递归
归并排序和快排的不同点:
- 1,先分解再合并:归并排序先递归分解到最小粒度,然后从小粒度开始合并排序,自下而上的合并排序;
- 2,边分解边排序:快速排序每次分解都实现整体上有序,即参照值左侧的数都小于参照值,右侧的大于参照值;是自上而下的排序;
- 3,归并排序不是原地排序,因为两个有序数组的合并一定需要额外的空间协助才能合并;
- 4,快速排序是原地排序,原地排序指的是空间复杂度为O(1);
- 5,归并排序每次将数组一分为二,快排每次将数组一分为三
数据结构大题注意点!!!(评分标准)
以下是本文第一题的评分标准!当在一定紧急情况下,可以断臂求生,没必要得到最优解(除非自己脑子非常清楚能写出来),先把该拿的分数拿到,然后将可能拿到的分拿到!