【追求卓越09】算法--散列表（哈希表）-编程知识

引导

通过前面几个章节的学习（二分查找，跳表），我们发现想要快速查找某一个元素，首先需要将所有元素进行排序，再利用二分法思想进行查找，复杂度是O(logn)。有没有更快的查找方式呢？

本章介绍一下我们工作中经常接触到的散列表（哈希表）。它能够使查找的效率达到O(1)。主要是理论方面，让大家开始了解哈希思想。

散列表

提到查找复杂度是O(1)，我们在前面接触到的就是数组了。散列思想就是基于数组支持下标随机访问数据特想实现的。那么问题就是如何将元素和数组下标进行映射？

例：学校开运动会，有100个运动员，编号是0~99。我要查找86号运动员的信息，该怎么做呢？

思路：我们可以建立一个数组，将标号和数组下标一一对应，访问哪一个标号的运动员，直接查找对应数组下标即可。

该散列思想中，编号我们称作为键或者关键字。将关键字转换为数组下标的，我们称作为散列函数。而散列函数计算得到的值就叫做散列值（数组下标）。

散列思想：散列表用的就是数组支持按照下标随机访问。当我们通过散列函数将元素的键值映射为数组下标时，然后将数组保存到数组对应位置中。当我们查找都一个元素时，我们使用同一个散列函数，将键值转化为数组下标，从对应的数组下标获取数据。

散列函数

从散列思想中，我们可以知道散列表中散列函数起到很重要的作用。针对不同的问题，散列函数都可能不同。比如上面的例子，我可以设置这样的哈希函数：

int hash(int key)
{
return key;
}
/*将关键字作为下标*/

由于该例子较为简单，也比较容易想到。但是无论什么想的问题，我觉得散列函数应该尽量做到一下几点：

散列函数计算得到的散列值是一个非负整数。因为散列值会作为数组下标。
如果key1 == key2,那么hash(key1)==hash(key2)。
如果key1 != key2,那么hash(key1)!=hash(key2)。

其中1，2好理解，但是3实际上是很实现的。因为数组的大小是有限的，但是不同元素可能会有很多。这就导致肯定会存在key1 != key2,hash(key1)==hash(key2)的情况。这种情况我们称之为散列冲突。再优秀的散列函数也避免不了散列冲突。

散列冲突的解决方式

散列冲突的解决方式有两种：开放寻址法，链表法。

开放寻址法

开放寻址法的思想是：出现了散列冲突，我们就重新探测到一个空闲位置，将其插入。

如何探测空闲位置？

如果某个数据经过散列函数之后，存储位置已经被占用了，我们就从当前位子开始，依次往后查找，看是否有空闲位子，直到找到为止。

如何查找？

通过散列函数求出要查找出的键值对应的散列值，然后比较数组中下标为散列值的元素和要查找的元素。如果相等，则说明是我们要找的元素；否则继续往后查找。如果遍历到空闲位子，还没有找到，则说明散列表中没有要查找的元素。

删除的注意事项？

我们知道散列表有查找操作肯定也有删除操作。当我们删除一个元素时，如果将其设置为空闲，那么在查找的过程中就会出现问题（原本在散列表中的元素，会认定为不存在）。我们可以将删除的元素置为delete状态。该状态的位子，可以插入数据。查找的时候，不必停下来，继续向后查找。

开放寻址法的缺点?

从开放寻址法的思想中，我们可以考虑到，当散列表中的元素越来越多的时候，散列冲突可能性越来越大，空闲位置越来越少，线性探测的时间就会越来越久。极端情况下，我们可能需要探测整个散列表，最坏的情况下，时间复杂度是O(n)。

装载因子

一般情况下，我们会尽量保证散列表中有一定比例的空闲槽位，我们用装载因子表示空位的多少。

散列表的装载因子=填入表中的元素个数/散列表的长度

链表法

链表法相对于开发寻址法较为简单，也容易理解。使用的是指针数组结构。数组元素对应的是一个链表，所有散列值相同的元素都在一个链表中。如图：

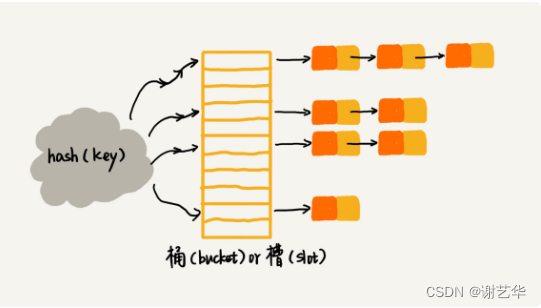
那么链表法的插入操作，我们选择链表的头插，所以时间复杂度是O(1)。

但是查找和删除操作的时间复杂度是O(k),k表示链表的长度。理论上每个链表的长度应该是均匀的，k=n/m。m是散列表的长度。这就要求散列表的优秀。若散列表不够好，那么查找和删除的复杂度可能会退化到O(n)。

如何设计散列函数

我们知道散列函数是散列表中重要的一个部分，它的好坏，决定了散列冲突的概率以及散列表的性能。

散列函数在设计的时候除了尽量遵循，上章节中指明的三点，还要考虑下面几点因素：

散列函数不能设计的太复杂。复杂的散列函数会消耗过多的资源，间接影响性能。
散列值尽量随机并且分布均匀。这样才能降低散列冲突的概率，即使出现散列冲突，每个链表长度也比较均匀（针对链表法）

常见的散列函数的设计方法：数据分析法，直接寻址法，平方取中法，折叠法，随机数法等。

装载因子调整

我们知道当装载因子过大的时候，说明散列表中的元素越多，空闲位置越少，散列冲突的概率就会越大。

对于没有频繁插入和删除的静态散列表，我们可以设计出一个完美的散列表。因为数据都是我们提前已知的。

但是对于动态的散列表，数据集合是动态变化的。我们无法事先申请一个足够大的散列表。但是当装载因子逐渐变大，散列冲突变得无法接受的时候，我们就需要动态扩容。

比如当散列表的装载因子是0.8时，我们将散列表扩容一倍，那么装载因子就变为了0.4。仅仅将散列表扩容就可以吗？

散列表扩容之后，我们需要将原先的散列表拷贝到新的散列表中。这个过程需要重新进行散列函数计算。

问题：我们知道在扩容的时候，涉及到数据的搬移，这会消耗很多时间。这就导致响应不及时。该如何处理？

解：这种动态扩容，直接将数据进行搬移的方式，非常的耗时，用户体验很不好（出现概率较低）。我们可以进行优化，将数据搬移的操作进行分批处理。第一次进行扩容，我们只申请散列表，并将数据插入，不进行数据的搬移。当下次再插入数据时，我们从旧的散列表中拷贝一个到新的散列表（旧的delete）。一直当旧的散列表全部被搬移完。在这个过程中，我们查询时，需要先旧的散列表中查询，查询不到，再到新的散列表中查询。如果都没有，说明不存在。这种均摊的方式，将任何情况下，插入操作的时间复杂度是O(1);