【采用有限元法技术计算固有频率和欧拉屈曲荷载】使用有限元法的柱子的固有频率和屈曲荷载（Matlab代码实现）-编程知识

【采用有限元法技术计算固有频率和欧拉屈曲荷载】使用有限元法的柱子的固有频率和屈曲荷载（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

有限元法是一种常用的数值分析方法，用于求解结构的固有频率和屈曲荷载。下面简要概述使用有限元法分析柱子的固有频率和屈曲荷载的过程。

1. 建立几何模型：首先，根据柱子的实际几何形状，例如长度、截面形状和尺寸等，建立几何模型。通常使用三维空间中的节点和单元来离散化柱子的几何形状。

2. 材料建模：对柱子的材料进行建模，确定材料的弹性模量、泊松比等力学参数。这些参数对柱子的固有频率和屈曲荷载有重要影响。

3. 约束条件和荷载：定义柱子的边界条件，包括支撑点的约束和受力情况。对于求解固有频率，可以施加零荷载，而对于求解屈曲荷载，需要施加合适的压缩或弯曲荷载。

4. 划分单元和建立刚度矩阵：将柱子划分为小的单元，例如线性三角形单元或四边形单元。根据单元的几何形状、材料性质和边界条件，建立单元的刚度矩阵。通过组装所有单元的刚度矩阵，得到整个柱子的刚度矩阵。

5. 求解固有频率：对于固有频率的求解，需要在刚度矩阵中施加边界条件，并将刚度矩阵转化为广义特征值问题。通过求解该特征值问题，可以得到柱子的固有频率和对应的振型。

6. 求解屈曲荷载：对于屈曲荷载的求解，可以使用静力分析或线性稳定性分析。在静力分析中，通过施加逐渐增大的荷载并观察柱子的变形和应力，确定柱子的屈曲荷载。在线性稳定性分析中，通过求解柱子的特征值问题，得到柱子的临界屈曲荷载。

以上是使用有限元法分析柱子固有频率和屈曲荷载的概述。这个过程涉及到离散化、材料建模、边界条件施加、刚度矩阵的建立、求解特征值问题等步骤。通过数值计算，可以获得柱子的固有频率和屈曲荷载，从而评估柱子的结构性能和安全性。需要注意，具体的应用案例和算法细节可能因具体问题而有所不同，建议在具体分析中参考专业的有限元分析软件和相关工具的使用指南和文献。

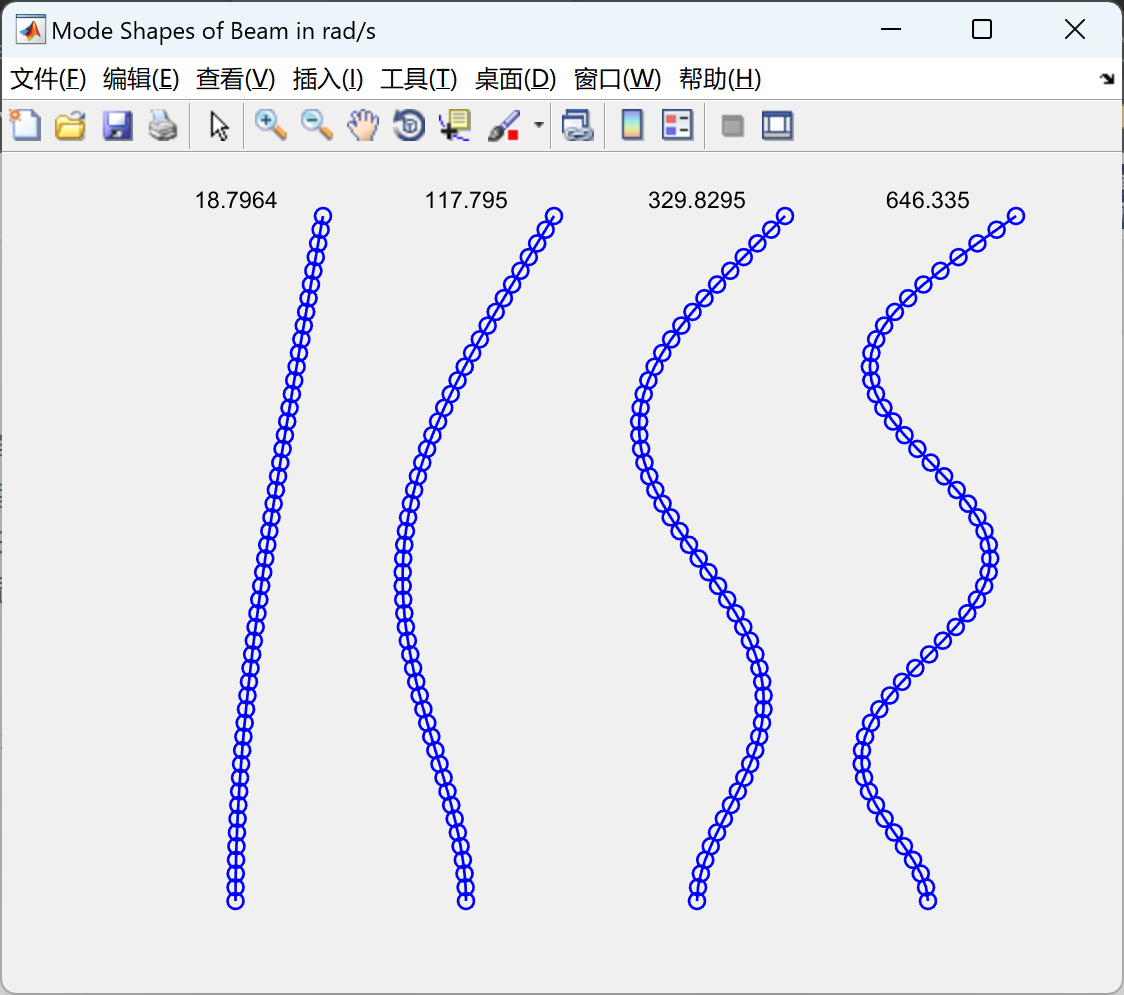
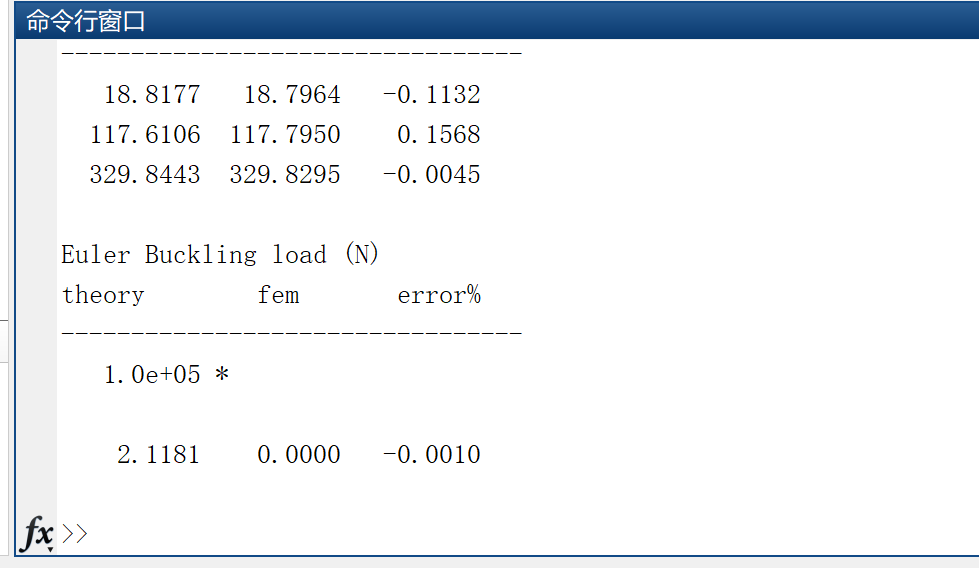
本文使用有限元技术计算固有频率和欧拉屈曲载荷。埃尔米特梁单元用作插值函数。计算并求解特征值的装配质量、几何刚度矩阵和刚度矩阵。绘制前四个振型。考虑了四种不同的边界条件。根据用户对杨氏模量的要求，可以更改单元数、单位长度质量和边界。使用FEM获得的值与理论值进行比较，并显示误差百分比。得到的值与理论值非常吻合。使用更多数量的元素可以提高精度。

📚2 运行结果

部分代码：

% Variable descriptions %
% k = element stiffness matrix %
% kg = element geometric stiffness matrix %
% m = element mass matrix %
% kk = system stiffness matrix %
% kkg = system geometric stiffness matrix %
% mm = system mass matrix %
% index = a vector containing system dofs associated with each element %
% %
%----------------------------------------------------------------------------%

clear
clc

disp('please wait!!!!!!-The job is under run')

% Discretizing the Beam

nel=50; % number of elements
nnel=2; % number of nodes per element
ndof=2; % number of dofs per node
nnode=(nnel-1)*nel+1; % total number of nodes in system
sdof=nnode*ndof; % total system dofs

% Material properties
E=2.1*10^11; % Youngs modulus
I=2003.*10^-8; % moment of inertia of cross-section
mass = 61.3; % mass density of the beam
tleng = 7.; % total length of the beam
leng = tleng/nel; % uniform mesh (equal size of elements)
lengthvector = 0:leng:tleng ;
% Boundary Conditions
bc = 'c-f' ; % clamped-free
%bc = 'c-c' ; % clamped-clamped
%bc = 'c-s' ; % clamped-supported
%bc = 's-s' ; % supported-supported

kk=zeros(sdof,sdof); % initialization of system stiffness matrix
kkg=zeros(sdof,sdof); % initialization of system geomtric stiffness matrix
mm=zeros(sdof,sdof); % initialization of system mass matrix
index=zeros(nel*ndof,1); % initialization of index vector