线性最小二乘问题
m个方程求解n个未知数，有三种情况：
- m=n且A为非奇异，则有唯一解，x=A.inverse()*b
- m>n，约束的个数大于未知数的个数，称为超定问题（overdetermined）
- m<n，负定/欠定问题（underdetermined）
通常我们遇到的都是超定问题，此时Ax=b的解是不存在的，从而转向解最小二乘问题：
J(x)为凸函数，一阶导数为0，得到：
,称之为正规方程
一般解：
奇异值分解与线性最小二乘问题
设
列满秩，A的奇异值分解:（公式1）
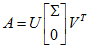
其中U和V为半酉阵，分别满足
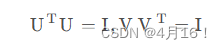
其中，这里的几个符号的大小：U:mm
:nn V:n
n
注意：为什么这里是nn，是因为我上面写的公式1中UGV，G=
，G的尺寸是mn
为 U 的 前 n 列矩阵，即
则：
等号当且仅
时成立，所以：
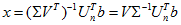
这就是我们千辛万苦要求的线性最小二乘问题的解！！！
用eigen库计算的例子：
//Ax=bMatrixXd A= MatrixXd::Zero(15,8);Eigen::JacobiSVD<MatrixXd> svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);Eigen::Matrix<double, 15, 15> U = svd.matrixU();Eigen::Matrix<double, 8, 8> V = svd.matrixV();Eigen::Matrix<double, 8, 8> Gama = svd.singularValues().asDiagonal();Eigen::Matrix<double, 15, 1> b;Eigen::Matrix<double, 8, 1> x = V * Gama.inverse()*(U.block<15,8>(0,0).transpose())*b;
