摘要:多项式回归(Polynomial Regression)是一种回归分析方法,通过拟合一个多项式方程来模拟自变量与因变量之间的非线性关系。多项式回归的目标是找到一组多项式系数,使得拟合曲线尽可能地接近数据点。这种方法可以用于预测、设计和推理、其他数据分析任务。多项式回归是一种统计学和机器学习领域常用的回归分析方法,属于线性回归的一种形式,将自变量x和因变量y之间的关系建模为n次多项式。

目前求解多项式回归问题,主要是把多项式回归转化成线性回归并用最小二乘法得到损失函数,令偏导等于0来求解。另外也可以直接使用梯度下降等方法来最小化损失函数。这些优化技术的时间复杂度是多项式级别的,随着问题规模的增长,很难在短时间找到满意的解。
鉴于摩尔定律即将走到尽头,就要探索非常规计算范式(如量子计算)解决大规模优化问题的适用性。量子计算机擅长解决困难的优化问题,并为加速求解问题提供了更快、更精准有效的替代方案。
在场景应用上,多项式回归分析可用来估计功率失配问题。如孤岛配电系统减载的策略用例上,精准制定负载优先级以准确估计频率失衡问题,稳定系统频率,高效克服配电系统因分布式发电(DG)集成而带来的系统稳定性不足造成的停电等问题。此外,在炼钢场景下,如将生铁和回收废料的混合物还原为低碳钢,对这一过程的预测及演变能力操作员可以通过过程目标预测系统来增强。而多项式分析方法就可以从过程参数的较小子集来预测过程,对复杂预测模型实现高精确推理。
同样,在预测农作物产量和降雨量的关系、每日用水量预测、光伏发电预测等场景下,多项式回归分析都能高度适配。
5月16日,北京玻色量子科技有限公司(以下简称“玻色量子”)在新品发布会上推出的100量子比特相干光量子计算机真机——“天工量子大脑”🔗,旨在快速、高效地求解NP-hard的Ising问题。而多项式回归系数的拟合就可以转化为一个Ising/QUBO模型,由“天工量子大脑”快速求解。“天工量子大脑”可以极大简化求解步骤并在毫秒级的时间里给出较好的拟合系数取值。同时,多项式回归是机器学习领域的基础问题,量子计算可以在统计学和机器学习领域的其他问题发挥更好的效果。
建模思路
首先给出符号的定义:
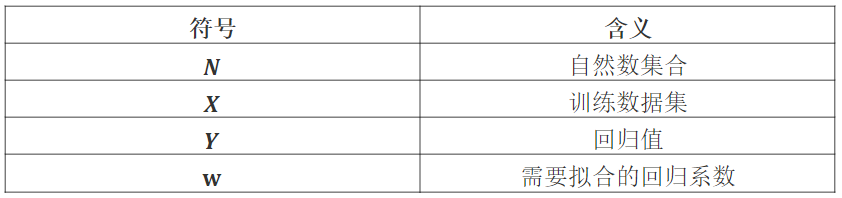
下面是多项式回归的原问题,其中d为多项式的次数
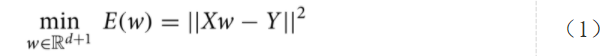
为了将多项式回归问题转换为QUBO形式,我们先将(1)式进行改写
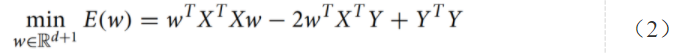
接着,引入一个精度向量P=[p1,p2,...,pk]T,k∈N。p中的每个项可以是2的整数次幂,幂指数可以为正也可以为负。同时,引入k个二元变量
![]()
则每个系数w可以表示为:
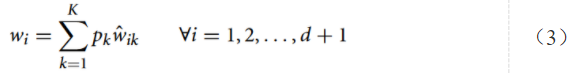
式(3)可以用矩阵表示如下
![]()
式(4)带入式(2)替换后可得
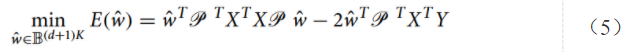
该问题本身没有额外约束,我们已经将问题的变量进行二值化处理,式(5)即为多项式回归的QUBO模型。
案例求解
我们以如下三次曲线为例进行多项式回归分析,

通过在目标值y中加入符合正态分布的随机噪声, 生成的随机样本图像如图1所示。
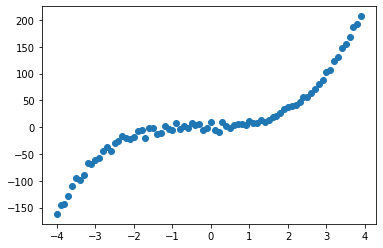
图1 三次曲线随机样本
在本案例中,回归系数w=[w0,w1,w2],即
![]()
我们可以设置P=[21,20,2-1,...,2-4],每个系数设置6个比特,共设置18个比特,求解后可以得到
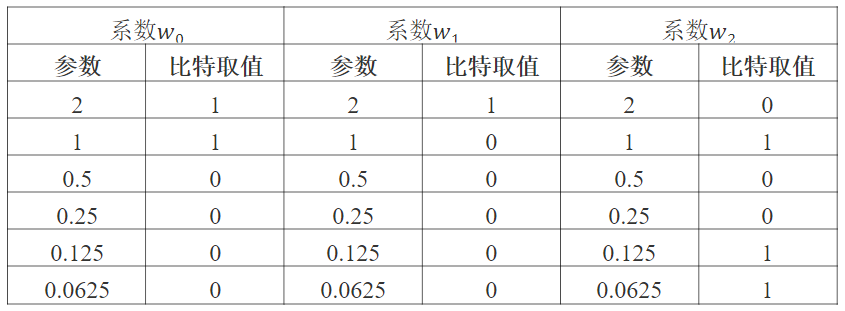
所以,各个系数取值结果如下:
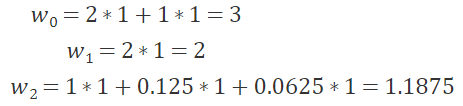
拟合结果如图2所示。
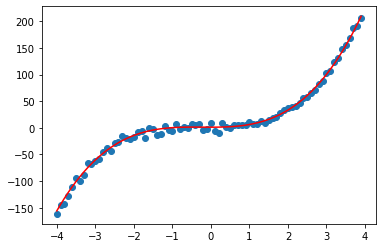
图2 拟合结果
问题拓展
多项式回归是机器学习等领域的基础的问题,量子计算还可以在机器学习的其他问题中发挥优势。
未来,玻色量子将依托100计算量子比特相干光量子计算机真机——“天工量子大脑”,聚焦“实用化量子计算”,不断深入研究包括NP-Complete问题在内的众多问题,拓展更多可实用化量子计算的真实应用场景。
玻色量子还将启动“燎原计划”开发者平台,并持续对外开放“天工量子大脑”的真机测试,热忱欢迎更多不同领域的研究伙伴前来了解相干量子计算的原理和能力,在此基础上展开共同研发,用量子计算去解决更多真实场景中的问题,让量子计算的超强算力能真正服务于各行各业,满足未来时代对于计算的需求。
[参考文献]
[1] Date P, Potok T. Adiabatic quantum linear regression[J]. Scientific reports, 2021, 11(1): 21905.
[2] 百度百科
https://baike.baidu.com/item/%E7%BA%BF%E6%80%A7%E5%9B%9E%E5%BD%92/8190345?fr=aladdin