前言:在学习紧组合之前学会GNSS/INS松组合是很有必要的,i2NAV团队开源的KF_GINS项目可以作为GNSS/INS松组合学习模板,本文章主要对武汉大学i2NAV发布的PPP/INS紧组合学习资源进行算法层面的总结,链接:
武汉大学多源智能导航实验室 (i2nav.cn)
一、GNSS相位观测方程
 这个地方需要注意到在观测方程中减去了整周模糊度*波长,也是我觉得在物理意义上比较好理解的形式,而在大多数GNSS相位观测方程中是这种形式的:
这个地方需要注意到在观测方程中减去了整周模糊度*波长,也是我觉得在物理意义上比较好理解的形式,而在大多数GNSS相位观测方程中是这种形式的:
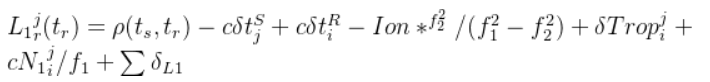
在这套紧组合学习方案中,PPP模型选用了无电离层模型,如下:

在初始位置按泰勒级数展开:


联系误差方程:v=BX-l,参数有测站三维坐标,接收机钟差,对流层湿延迟,组合浮点模糊度,而在伪距观测方程中则包括了码偏(TGD)参数。

但是存在秩亏现象,将伪距偏差归算到接收机钟差中,得到最终误差方程。

观测方程: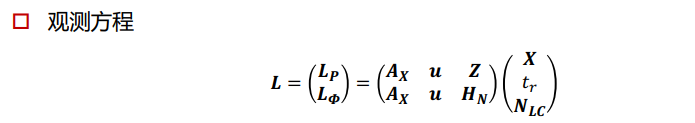
因为将位置误差和接收机钟差建模为白噪声(即与时间无关的误差),将对流层湿延迟建模为随机游走噪声,浮点模糊度为常数,得到如下状态方程。
状态方程:

什么是白噪声和随机游走噪声:
时间序列R语言操作2——白噪声和随机游走模型_r语言随机游走序列生成-CSDN博客
概率统计笔记:白噪声与随机游走_随机游走噪声-CSDN博客
无论是扩展卡尔曼滤波还是图优化的方式,都是从观测方程和状态方程这两个基本方程进行解算。
二、惯导误差方程
在i2NAV实验室网站中有详细的惯导学习资源,至少要做到了解下面参数和不同坐标系转换的水平。
误差方程:

状态方程:
 杆臂效应改正: 将INS解算得到的IMU中心通过旋转平移得到GNSS测量中心
杆臂效应改正: 将INS解算得到的IMU中心通过旋转平移得到GNSS测量中心
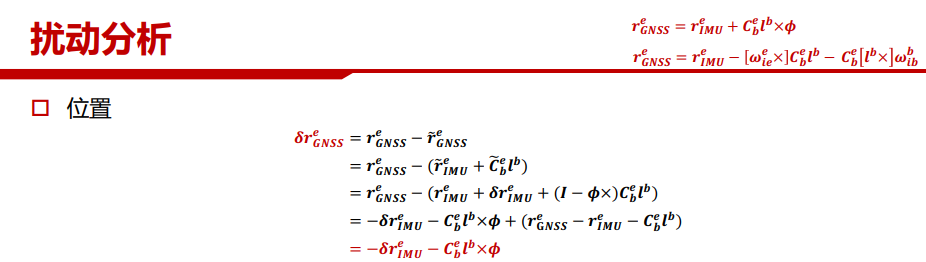
即GNSS微分位置参数=GNSS测量值-INS杆臂改正后的测量值,将右上角的式子代入解算过程得到最终结果。
三、PPP/INS紧组合
观测方程:
状态方程:
GNSS/INS观测方程共有参数:IMU位置,速度,姿态3*3=9个参数
IMU特有参数:陀螺仪零偏,加速度计零偏,陀螺仪比例因子,加速度计比例因子4*3=12
GNSS特有参数:对流层湿延迟,接收机钟差(加入了码偏),组合浮点模糊度2+m
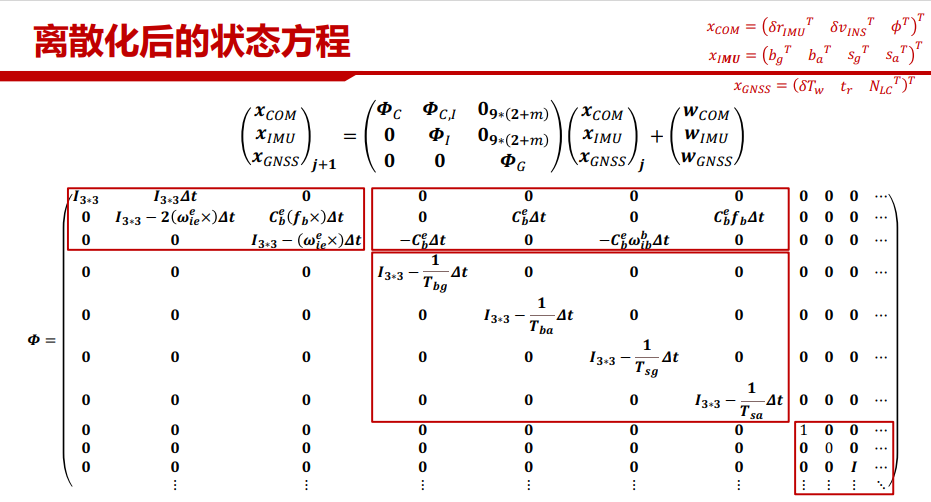 +
+
可以看到GNSS特有参数的系数阵中,接收机钟差对应0,其余对应单位阵。

联合状态方程与观测方程后,其形式更加接近我们所熟知的最小二乘,卡尔曼滤波本质上就是最小二乘。
四、松组合与紧组合流程