基于C#实现线段树-编程知识

一、线段树

线段树又称"区间树”，在每个节点上保存一个区间，当然区间的划分采用折半的思想，叶子节点只保存一个值，也叫单元节点，所以最终的构造就是一个平衡的二叉树，拥有 CURD 的 O(lgN)的时间。

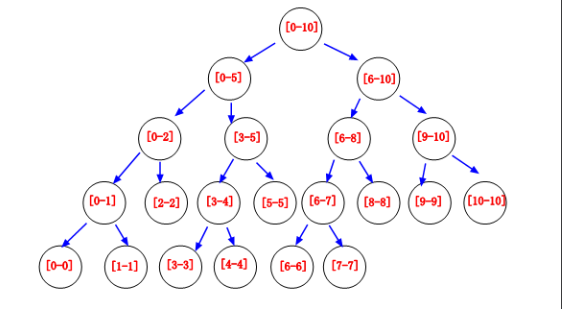
从图中我们可以清楚的看到[0-10]被划分成线段的在树中的分布情况，针对区间[0-N]，最多有 2N 个节点，由于是平衡二叉树的形式也可以像堆那样用数组来玩，不过更加耗费空间，为最多 4N 个节点，在针对 RMQ 的问题上，我们常常在每个节点上增加一些 sum，max，min 等变量来记录求得的累加值，当然你可以理解成动态规划的思想，由于拥有 logN 的时间，所以在 RMQ 问题上比数组更加优美。

二、代码

1、在节点中定义一些附加值，方便我们处理 RMQ 问题。

 #region 线段树的节点/// <summary>/// 线段树的节点/// </summary>public class Node{/// <summary>/// 区间左端点/// </summary>public int left;/// <summary>/// 区间右端点/// </summary>public int right;/// <summary>/// 左孩子/// </summary>public Node leftchild;/// <summary>/// 右孩子/// </summary>public Node rightchild;/// <summary>/// 节点的sum值/// </summary>public int Sum;/// <summary>/// 节点的Min值/// </summary>public int Min;/// <summary>/// 节点的Max值/// </summary>public int Max;}#endregion

2、构建(Build)
前面我也说了，构建有两种方法，数组的形式或者链的形式，各有特点，我就采用后者，时间为 O(N)。

  #region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="length"></param>public Node Build(int[] nums){this.nums = nums;return Build(nodeTree, 0, nums.Length - 1);}#endregion#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="left"></param>/// <param name="right"></param>public Node Build(Node node, int left, int right){//说明已经到根了，当前当前节点的max，sum，min值（回溯时统计上一层节点区间的值）if (left == right){return new Node{left = left,right = right,Max = nums[left],Min = nums[left],Sum = nums[left]};}if (node == null)node = new Node();node.left = left;node.right = right;node.leftchild = Build(node.leftchild, left, (left + right) / 2);node.rightchild = Build(node.rightchild, (left + right) / 2 + 1, right);//统计左右子树的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;return node;}#endregion

3、区间查询
在线段树中，区间查询还是有点小麻烦的，存在三种情况。
① 完全包含：也就是节点的线段范围完全在查询区间的范围内，这说明我们要么到了“单元节点",要么到了一个子区间，这种情况就是我找到了查询区间的某一个子区间，直接累积该区间值就可以了。
② 左交集：这种情况我们需要到左子树去遍历。
③ 右交集：这种情况我们需要到右子树去遍历。
比如说：我要查询 Sum[4-8]的值,最终会成为:Sum 总=Sum[4-4]+Sum[5-5]+Sum[6-8]，时间为 log(N)。

 #region 区间查询/// <summary>/// 区间查询(分解)/// </summary>/// <returns></returns>public int Query(int left, int right){int sum = 0;Query(nodeTree, left, right, ref sum);return sum;}/// <summary>/// 区间查询/// </summary>/// <param name="left">查询左边界</param>/// <param name="right">查询右边界</param>/// <param name="node">查询的节点</param>/// <returns></returns>public void Query(Node node, int left, int right, ref int sum){//说明当前节点完全包含在查询范围内，两点：要么是单元节点，要么是子区间if (left <= node.left && right >= node.right){//获取当前节点的sum值sum += node.Sum;return;}else{//如果当前的left和right 和node的left和right无交集，此时可返回if (node.left > right || node.right < left)return;//找到中间线var middle = (node.left + node.right) / 2;//左孩子有交集if (left <= middle){Query(node.leftchild, left, right, ref sum);}//右孩子有交集if (right >= middle){Query(node.rightchild, left, right, ref sum);}}}#endregion

4、更新操作
这个操作跟树状数组中的更新操作一样，当递归的找到待修改的节点后，改完其值然后在当前节点一路回溯，并且在回溯的过程中一路修改父节点的附加值直到根节点，至此我们的操作就完成了，复杂度同样为 logN。

 #region 更新操作/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(int index, int key){Update(nodeTree, index, key);}/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(Node node, int index, int key){if (node == null)return;//取中间值var middle = (node.left + node.right) / 2;//遍历左子树if (index >= node.left && index <= middle)Update(node.leftchild, index, key);//遍历右子树if (index <= node.right && index >= middle + 1)Update(node.rightchild, index, key);//在回溯的路上一路更改，复杂度为lgNif (index >= node.left && index <= node.right){//说明找到了节点if (node.left == node.right){nums[index] = key;node.Sum = node.Max = node.Min = key;}else{//回溯时统计左右子树的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;}}}#endregion

最后我们做个例子，在 2000000 的数组空间中，寻找 200-3000 区间段的 sum 值，看看他的表现如何。

 using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Diagnostics;using System.Threading;using System.IO;namespace ConsoleApplication2{public class Program{public static void Main(){int[] nums = new int[200 * 10000];for (int i = 0; i < 10000 * 200; i++){nums[i] = i;}Tree tree = new Tree();//将当前数组构建成 “线段树”tree.Build(nums);var watch = Stopwatch.StartNew();var sum = tree.Query(200, 3000);watch.Stop();Console.WriteLine("耗费时间:{0}ms,  当前数组有:{1}个数字, 求出Sum=:{2}", watch.ElapsedMilliseconds, nums.Length, sum);Console.Read();}}public class Tree{#region 线段树的节点/// <summary>/// 线段树的节点/// </summary>public class Node{/// <summary>/// 区间左端点/// </summary>public int left;/// <summary>/// 区间右端点/// </summary>public int right;/// <summary>/// 左孩子/// </summary>public Node leftchild;/// <summary>/// 右孩子/// </summary>public Node rightchild;/// <summary>/// 节点的sum值/// </summary>public int Sum;/// <summary>/// 节点的Min值/// </summary>public int Min;/// <summary>/// 节点的Max值/// </summary>public int Max;}#endregionNode nodeTree = new Node();int[] nums;#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="length"></param>public Node Build(int[] nums){this.nums = nums;return Build(nodeTree, 0, nums.Length - 1);}#endregion#region 根据数组构建“线段树"/// <summary>/// 根据数组构建“线段树"/// </summary>/// <param name="left"></param>/// <param name="right"></param>public Node Build(Node node, int left, int right){//说明已经到根了，当前当前节点的max，sum，min值（回溯时统计上一层节点区间的值）if (left == right){return new Node{left = left,right = right,Max = nums[left],Min = nums[left],Sum = nums[left]};}if (node == null)node = new Node();node.left = left;node.right = right;node.leftchild = Build(node.leftchild, left, (left + right) / 2);node.rightchild = Build(node.rightchild, (left + right) / 2 + 1, right);//统计左右子树的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;return node;}#endregion#region 区间查询/// <summary>/// 区间查询(分解)/// </summary>/// <returns></returns>public int Query(int left, int right){int sum = 0;Query(nodeTree, left, right, ref sum);return sum;}/// <summary>/// 区间查询/// </summary>/// <param name="left">查询左边界</param>/// <param name="right">查询右边界</param>/// <param name="node">查询的节点</param>/// <returns></returns>public void Query(Node node, int left, int right, ref int sum){//说明当前节点完全包含在查询范围内，两点：要么是单元节点，要么是子区间if (left <= node.left && right >= node.right){//获取当前节点的sum值sum += node.Sum;return;}else{//如果当前的left和right 和node的left和right无交集，此时可返回if (node.left > right || node.right < left)return;//找到中间线var middle = (node.left + node.right) / 2;//左孩子有交集if (left <= middle){Query(node.leftchild, left, right, ref sum);}//右孩子有交集if (right >= middle){Query(node.rightchild, left, right, ref sum);}}}#endregion#region 更新操作/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(int index, int key){Update(nodeTree, index, key);}/// <summary>/// 更新操作/// </summary>/// <param name="index"></param>/// <param name="key"></param>public void Update(Node node, int index, int key){if (node == null)return;//取中间值var middle = (node.left + node.right) / 2;//遍历左子树if (index >= node.left && index <= middle)Update(node.leftchild, index, key);//遍历右子树if (index <= node.right && index >= middle + 1)Update(node.rightchild, index, key);//在回溯的路上一路更改，复杂度为lgNif (index >= node.left && index <= node.right){//说明找到了节点if (node.left == node.right){nums[index] = key;node.Sum = node.Max = node.Min = key;}else{//回溯时统计左右子树的值(min，max，sum)node.Min = Math.Min(node.leftchild.Min, node.rightchild.Min);node.Max = Math.Max(node.leftchild.Max, node.rightchild.Max);node.Sum = node.leftchild.Sum + node.rightchild.Sum;}}}#endregion}}