摘要:旅行商问题(Traveling Salesman Problem,TSP)是一个经典的组合优化问题。经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总行程最短。
从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的Hamilton回路。TSP问题是一例典型的NP-Hard问题,该问题的可行解是所有顶点的全排列,随着顶点数的增加,会产生组合爆炸,因此精确求解此问题是相当困难的。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛应用,国内外学者对其进行了大量研究。

早期研究者使用精确算法求解TSP问题,常用的方法包括:分支定界、线性规划、动态规划等。但是,随着问题规模的增大,精确算法将变得无能为力。因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法,主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。
最早的TSP问题的数学规划是由Dantzig(1959)等人提出,并且在最优化领域中进行了深入研究。许多优化方法都用它作为一个测试基准。尽管问题在计算上很困难,但已经有了大量的启发式算法和精确方法来求解问题节点规模上万的实例,并且能将误差控制在1%内。TSP的研究历史很久,最早的描述是1759年欧拉研究的骑士环游问题,即对于国际象棋棋盘中的64个方格,走访64个方格一次且仅一次,并且最终返回到起始点。
该问题的研究有着广泛的应用场景,包括:如何规划最合理高效的道路交通,以减少拥堵;如何更好地规划物流,以减少运营成本;在互联网环境中如何更好地设置节点,以更好地让信息流动等。因此,该问题可以扩展并应用于物流、制造、遗传学和通信等领域,为开发建模技术和工具提供良好的计算基础。
在现实世界更为复杂的问题中,旅行商问题常常用于分销策略,自20世纪50年代以来,该问题的受欢迎程度急剧上升。例如,沃尔玛通过独特案例的分销策略,使其销售量约占市场总销量的88%,仓库方面的运输成本大幅降低5%等。持续致力于寻求最小化成本的扩张方法,让沃尔玛迅速崛起。
北京玻色量子科技有限公司在5月16日新品发布会上推出的100量子比特相干光量子计算机真机——“天工量子大脑”🔗,旨在快速、高效地求解NP-Hard的Ising模型。旅行商问题就可以转化为一个Ising/QUBO模型,“天工量子大脑”可以极大简化求解步骤并在毫秒级的时间里稳定地求得局部最优解,在某些场景下可以求得全局最优解。
问题描述
旅行商问题是一个NP-Hard问题。给定一张有权重的连接图G(V,E),其中V是点的集合,E是边的集合,要求遍历图上所有点再回到初始点,求路程最短的走法。
建模思路
我们使用邻接矩阵表示网络的连接情况,当两点间不存在边时,其权重值为0,令N=|V|。
引入0/1决策变量xu,j,令xu,j=1表示点u在第j个顺序被访问,否则xu,j=0,其中u∈{0,...,N-1},j∈{0,...,N-1}。
首先,对于每一个点u,有且仅有一个访问次序j,因此可得如下约束:
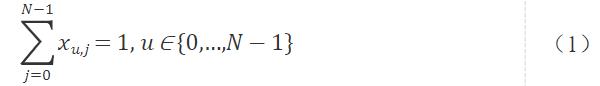
同样,对于每一个访问次序j,有且仅有一个点u,则有:
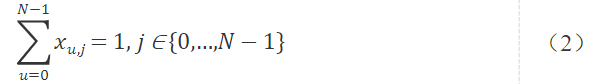
引入惩罚参数P,将式(1)、式(2)写成QUBO的惩罚项则有:
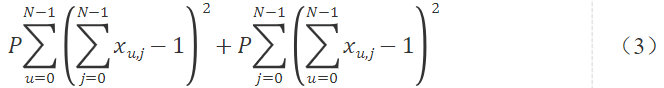
同时,对于(u,v)∉E,我们希望u,v不连续出现在次序j,j+1上,则有:
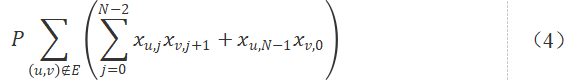
通过以上约束构建的QUBO模型惩罚项式(3)和式(4),我们可以构建一个遍历所有的点的路径的模型(又称哈密尔顿环):
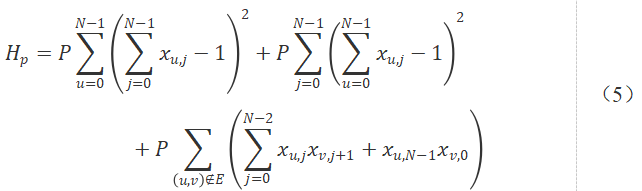
然而对于旅行商问题,在此基础上,我们想要获得上述路径中最短的一个,需要引入原模型目标函数。令wu,v为边的权重,则有:
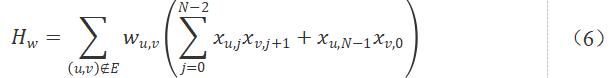
式(6)和式(5)相加即得到QUBO模型表达式:
![]()
我们用下面的例子来进一步分析。
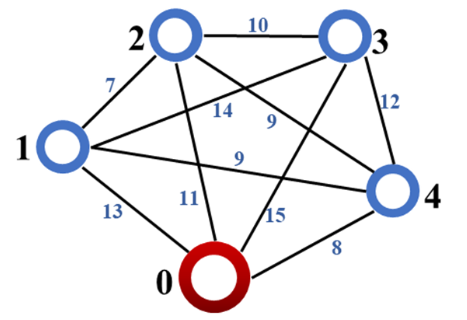
图1 旅行商问题案例示意图
图1给出了案例的示意图和参数,该案例包含5个节点,任意两点之间的距离用蓝色数字标出,可以得到该问题的wu,v边的权重如下。
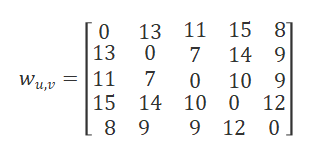
W将wu,v带入式(7)后即可得到QUBO模型,求解该模型,我们可以得到最优解x0,1=x4,2=x1,3=x2,4=x3,5=1,
其他决策变量为0,y=49,该最优解示意图如下图所示。
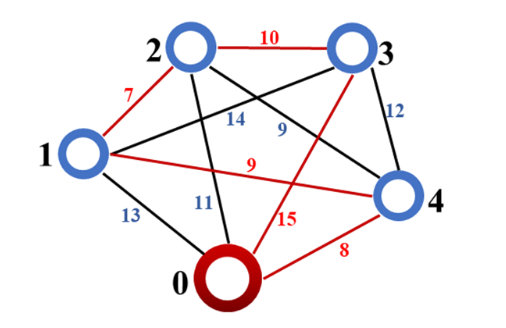
图2 最优解示意图(cost:49)
问题拓展
旅行商问题具有重要的实际意义和工程背景,一开始是为交通运输行业而被提出的,比如飞机航线安排、送邮件、快递服务、设计校车行进路线等等。之后在各个领域也发挥重要作用,如印制电路板转孔、天体成像卫星控制、电缆和光缆布线、晶体结构分析、数据串聚类等领域。但此类NP-Complete问题还没有找到一种多项式确定性算法解决。
未来,玻色量子将依托100量子比特相干光量子计算机真机——“天工量子大脑”,聚焦“实用化量子计算”,不断深入研究更多NP-Complete问题,拓展更多可实用化量子计算的真实应用场景。
玻色量子还将启动“燎原计划”开发者平台,并持续对外开放“天工量子大脑”的真机测试,热忱欢迎更多不同领域的研究伙伴前来了解相干量子计算的原理和能力,在此基础上展开共同研发,用量子计算去解决更多真实场景中的问题,让量子计算的超强算力能真正服务于各行各业,满足未来时代对于计算的需求。
参考资料
[1] Glover, Fred, Kochenberger, Gary, Du, Yu. Quantum Bridge Analytics I: a tutorial on formulating and using QUBO models[J]. 4OR: Quarterly Journal of the Belgian, French and Italian Operations Research Societies,2019,17(4):335-371. DOI:10.1007/s10288-019-00424-y.
[2]https://zh.wikipedia.org/wiki/%E6%97%85%E8%A1%8C%E6%8E%A8%E9%94%80%E5%91%98%E9%97%AE%E9%A2%98