python+gurobi求解线性规划、整数规划、0-1规划

文章目录

        • 简单回顾
        • 线性规划LP
        • 整数规划IP
        • 0-1规划

简单回顾

线性规划是数学规划中的一类最简单规划问题，常见的线性规划是一个有约束的，变量范围为有理数的线性规划。如：

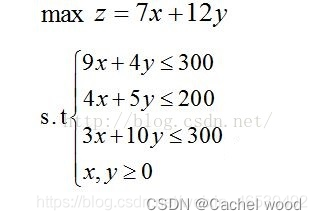
在这里插入图片描述
使用matlab的linprog函数即可求解简单的线性规划问题，可以参考这篇博客：
MATLAB求解线性规划（含整数规划和0-1规划）问题

matlab求解线性规划LP问题需要化为最小化问题，所有约束条件必须为≤类型，限制较多。本文介绍使用python+gurobi进行求解。
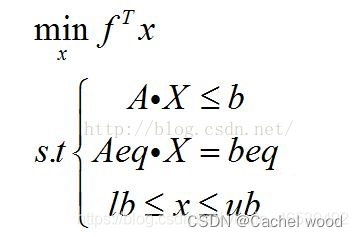
在这里插入图片描述
python+gurobi介绍参考这篇博客：
gurobi最新下载安装教程 2023.11

线性规划LP

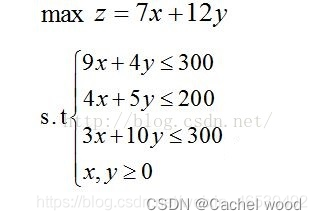
在这里插入图片描述

import gurobipy
from gurobipy import GRB# 创建模型
c = [7, 12]
a = [[9, 4],[4, 5],[3, 10]]
b = [300, 200, 300]
MODEL = gurobipy.Model("Example")# 创建变量
x = MODEL.addVars(2, lb=0, ub=gurobipy.GRB.INFINITY, name='x')# 更新变量环境
MODEL.update()# 创建目标函数
MODEL.setObjective(x.prod(c), gurobipy.GRB.MAXIMIZE)# 创建约束条件
MODEL.addConstrs(x.prod(a[i]) <= b[i] for i in range(3))# 执行线性规划模型
MODEL.optimize()
print("Obj:", MODEL.objVal)
for v in MODEL.getVars():print(f"{v.VarName}：{round(v.X,3)}")
Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 3 rows, 2 columns and 6 nonzeros
Model fingerprint: 0x6b25b35d
Coefficient statistics:Matrix range     [3e+00, 1e+01]Objective range  [7e+00, 1e+01]Bounds range     [0e+00, 0e+00]RHS range        [2e+02, 3e+02]
Presolve time: 0.01s
Presolved: 3 rows, 2 columns, 6 nonzerosIteration    Objective       Primal Inf.    Dual Inf.      Time0    3.2500000e+30   2.812500e+30   3.250000e+00      0s2    4.2800000e+02   0.000000e+00   0.000000e+00      0sSolved in 2 iterations and 0.01 seconds (0.00 work units)
Optimal objective  4.280000000e+02
Obj: 428.0
x[0]：20.0
x[1]：24.0

最终可得最优解为x = 20, y = 24, 最优值为428。
gurobi对最大化问题、最小化问题，大于等于和小于等于约束都支持。

整数规划IP

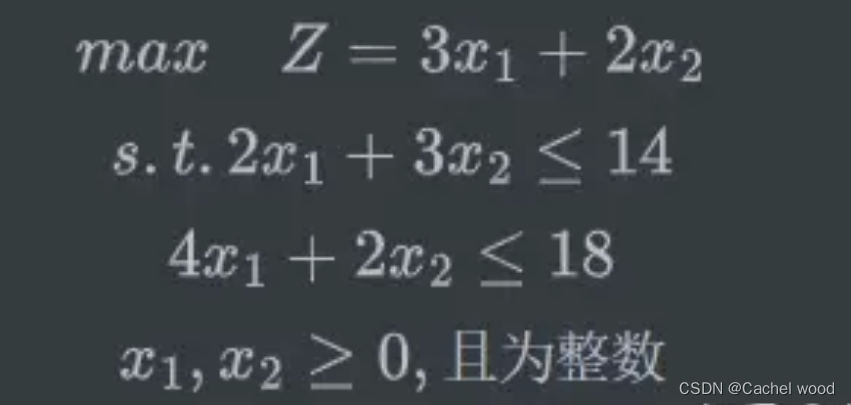
在这里插入图片描述

import gurobipy
from gurobipy import GRB
import numpy as np# 创建模型
c = [3, 2]
a = [[2, 3],[4, 2]]
b = [14, 18]
MODEL = gurobipy.Model("Example")# 创建变量
#x = MODEL.addVars(2, lb=0, ub=gurobipy.GRB.INFINITY, name='x')x1 = MODEL.addVar(vtype=GRB.INTEGER,lb=0,ub=GRB.INFINITY, name='x1')
x2 = MODEL.addVar(vtype=GRB.INTEGER,lb=0,ub=GRB.INFINITY, name='x2')
# 更新变量环境MODEL.update()# 创建目标函数
MODEL.setObjective(c[0]*x1+c[1]*x2, gurobipy.GRB.MAXIMIZE)# 创建约束条件
for i in range(2):MODEL.addConstr(a[i][0]*x1 + a[i][1]*x2 <= b[i])# 执行线性规划模型
MODEL.optimize()
print("Obj:", MODEL.objVal)
for v in MODEL.getVars():print(f"{v.VarName}：{round(v.X,3)}")

Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 2 rows, 2 columns and 4 nonzeros
Model fingerprint: 0x15a6e8bd
Variable types: 0 continuous, 2 integer (0 binary)
Coefficient statistics:Matrix range     [2e+00, 4e+00]Objective range  [2e+00, 3e+00]Bounds range     [0e+00, 0e+00]RHS range        [1e+01, 2e+01]
Found heuristic solution: objective 14.0000000
Presolve time: 0.00s
Presolved: 2 rows, 2 columns, 4 nonzeros
Variable types: 0 continuous, 2 integer (0 binary)Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)Solution count 1: 14 Optimal solution found (tolerance 1.00e-04)
Best objective 1.400000000000e+01, best bound 1.400000000000e+01, gap 0.0000%
Obj: 14.0
x1：4.0
x2：1.0

可得该整数规划问题的最优解为x1 = 4, x2 = 1,最优值为14。

如果解其对应的松弛问题：

import gurobipy
from gurobipy import GRB
import numpy as np# 创建模型
c = [3, 2]
a = [[2, 3],[4, 2]]
b = [14, 18]
MODEL = gurobipy.Model("Example")# 创建变量
x = MODEL.addVars(2, lb=0, ub=gurobipy.GRB.INFINITY, name='x')# 更新变量环境MODEL.update()# 创建目标函数
MODEL.setObjective(x.prod(c), gurobipy.GRB.MAXIMIZE)# 创建约束条件
MODEL.addConstrs(x.prod(a[i]) <= b[i] for i in range(2))# 执行线性规划模型
MODEL.optimize()
print("Obj:", MODEL.objVal)
for v in MODEL.getVars():print(f"{v.VarName}：{round(v.X,3)}")

Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 2 rows, 2 columns and 4 nonzeros
Model fingerprint: 0x15a42e7d
Coefficient statistics:Matrix range     [2e+00, 4e+00]Objective range  [2e+00, 3e+00]Bounds range     [0e+00, 0e+00]RHS range        [1e+01, 2e+01]
Presolve time: 0.01s
Presolved: 2 rows, 2 columns, 4 nonzerosIteration    Objective       Primal Inf.    Dual Inf.      Time0    5.0000000e+30   2.750000e+30   5.000000e+00      0s2    1.4750000e+01   0.000000e+00   0.000000e+00      0sSolved in 2 iterations and 0.01 seconds (0.00 work units)
Optimal objective  1.475000000e+01
Obj: 14.75
x[0]：3.25
x[1]：2.5

可以发现对应的解是x1 = 3.25, x2 = 2.5, 最优值为14.75。松弛问题的最优解总是优于整数规划问题的。

0-1规划

无论是matlab的linprog函数还是gurobi，0-1规划实际上只需要在整数规划的基础上，让决策变量的定义域在0-1之间即可。

仍然是上面的同一个问题：

##  0-1规划import gurobipy
from gurobipy import GRB# 创建模型
c = [3, 2]
a = [[2, 3],[4, 2]]
b = [14, 18]
MODEL = gurobipy.Model("Example")# 创建变量
#x = MODEL.addVars(2, lb=0, ub=gurobipy.GRB.INFINITY, name='x')x1 = MODEL.addVar(vtype=GRB.INTEGER,lb=0,ub=1, name='x1')
x2 = MODEL.addVar(vtype=GRB.INTEGER,lb=0,ub=1, name='x2')
# 更新变量环境MODEL.update()# 创建目标函数
MODEL.setObjective(c[0]*x1+c[1]*x2, gurobipy.GRB.MAXIMIZE)# 创建约束条件
for i in range(2):MODEL.addConstr(a[i][0]*x1 + a[i][1]*x2 <= b[i])# 执行线性规划模型
MODEL.optimize()
print("Obj:", MODEL.objVal)
for v in MODEL.getVars():print(f"{v.VarName}：{round(v.X,3)}")

Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 3 rows, 2 columns and 6 nonzeros
Model fingerprint: 0x6b25b35d
Coefficient statistics:Matrix range     [3e+00, 1e+01]Objective range  [7e+00, 1e+01]Bounds range     [0e+00, 0e+00]RHS range        [2e+02, 3e+02]
Presolve time: 0.01s
Presolved: 3 rows, 2 columns, 6 nonzerosIteration    Objective       Primal Inf.    Dual Inf.      Time0    3.2500000e+30   2.812500e+30   3.250000e+00      0s2    4.2800000e+02   0.000000e+00   0.000000e+00      0sSolved in 2 iterations and 0.01 seconds (0.00 work units)
Optimal objective  4.280000000e+02
Obj: 428.0
x[0]：20.0
x[1]：24.0
Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 3 rows, 6 columns and 18 nonzeros
Model fingerprint: 0x157f6a4a
Coefficient statistics:Matrix range     [9e+00, 6e+01]Objective range  [6e+00, 1e+01]Bounds range     [0e+00, 0e+00]RHS range        [6e+01, 2e+02]
Presolve time: 0.01s
Presolved: 3 rows, 6 columns, 18 nonzerosIteration    Objective       Primal Inf.    Dual Inf.      Time0    0.0000000e+00   4.187500e+01   0.000000e+00      0s3    2.9842520e+01   0.000000e+00   0.000000e+00      0sSolved in 3 iterations and 0.01 seconds (0.00 work units)
Optimal objective  2.984251969e+01
Obj: 29.84251968503937
x[0]：0.0
x[1]：0.433
x[2]：0.0
x[3]：4.252
x[4]：0.0
x[5]：0.0
Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 2 rows, 2 columns and 4 nonzeros
Model fingerprint: 0x15a6e8bd
Variable types: 0 continuous, 2 integer (0 binary)
Coefficient statistics:Matrix range     [2e+00, 4e+00]Objective range  [2e+00, 3e+00]Bounds range     [0e+00, 0e+00]RHS range        [1e+01, 2e+01]
Found heuristic solution: objective 14.0000000
Presolve time: 0.00s
Presolved: 2 rows, 2 columns, 4 nonzeros
Variable types: 0 continuous, 2 integer (0 binary)Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)Solution count 1: 14 Optimal solution found (tolerance 1.00e-04)
Best objective 1.400000000000e+01, best bound 1.400000000000e+01, gap 0.0000%
Obj: 14.0
x1：4.0
x2：1.0
Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 2 rows, 2 columns and 4 nonzeros
Model fingerprint: 0x15a42e7d
Coefficient statistics:Matrix range     [2e+00, 4e+00]Objective range  [2e+00, 3e+00]Bounds range     [0e+00, 0e+00]RHS range        [1e+01, 2e+01]
Presolve time: 0.01s
Presolved: 2 rows, 2 columns, 4 nonzerosIteration    Objective       Primal Inf.    Dual Inf.      Time0    5.0000000e+30   2.750000e+30   5.000000e+00      0s2    1.4750000e+01   0.000000e+00   0.000000e+00      0sSolved in 2 iterations and 0.01 seconds (0.00 work units)
Optimal objective  1.475000000e+01
Obj: 14.75
x[0]：3.25
x[1]：2.5
Gurobi Optimizer version 10.0.3 build v10.0.3rc0 (win64)CPU model: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz, instruction set [SSE2|AVX|AVX2]
Thread count: 4 physical cores, 8 logical processors, using up to 8 threadsOptimize a model with 2 rows, 2 columns and 4 nonzeros
Model fingerprint: 0xdff3d373
Variable types: 0 continuous, 2 integer (0 binary)
Coefficient statistics:Matrix range     [2e+00, 4e+00]Objective range  [2e+00, 3e+00]Bounds range     [1e+00, 1e+00]RHS range        [1e+01, 2e+01]
Found heuristic solution: objective 5.0000000Explored 0 nodes (0 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 1 (of 8 available processors)Solution count 1: 5 Optimal solution found (tolerance 1.00e-04)
Best objective 5.000000000000e+00, best bound 5.000000000000e+00, gap 0.0000%
Obj: 5.0
x1：1.0
x2：1.0

可得0-1规划的最优解是x1 = x2 = 1, 最优值 = 5。
当然0-1规划的典型应用场景是指派问题、运输问题、排班问题等。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/214339.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

全网最全图解Kafka适用场景

全网最全图解Kafka适用场景

消息系统 消息系统被用于各种场景&#xff0c;如解耦数据生产者&#xff0c;缓存未处理的消息。Kafka 可作为传统的消息系统的替代者&#xff0c;与传统消息系统相比&#xff0c;kafka有更好的吞吐量、更好的可用性&#xff0c;这有利于处理大规模的消息。 根据经验&#xff…
阅读更多...
『Postman入门万字长文』| 从工具简介、环境部署、脚本应用、Collections使用到接口自动化测试详细过程

『Postman入门万字长文』| 从工具简介、环境部署、脚本应用、Collections使用到接口自动化测试详细过程

『Postman入门万字长文』| 从工具简介、环境部署、脚本应用、Collections使用到接口自动化测试详细过程 1 Postman工具简介2 Postman安装3 Postman界面说明4 一个简单请求4.1 请求示例4.2 请求过程 5 Postman其他操作5.1 import5.2 History5.3 Environment5.4 Global5.5 其他变…
阅读更多...
java spring-boot 修改打包的jar包名称

java spring-boot 修改打包的jar包名称

修改pom文件 <finalName>lzwd</finalName><build><finalName>lzwd</finalName><plugins><plugin><groupId>org.springframework.boot</groupId><artifactId>spring-boot-maven-plugin</artifactId></plu…
阅读更多...
NX二次开发UF_CSYS_create_matrix 函数介绍

NX二次开发UF_CSYS_create_matrix 函数介绍

文章作者&#xff1a;里海 来源网站&#xff1a;https://blog.csdn.net/WangPaiFeiXingYuan UF_CSYS_create_matrix Defined in: uf_csys.h int UF_CSYS_create_matrix(const double matrix_values [ 9 ] , tag_t * matrix_id ) overview 概述 Creates a 3 x 3 matrix. 创建…
阅读更多...
【23真题】最简单的211！均分141分！

【23真题】最简单的211！均分141分！

今天分享的是23年河海大学863的信号与系统试题及解析。 我猜测是由于23年太简单&#xff0c;均分都141分&#xff0c;导致24考研临时新增一门数字信号处理&#xff01;今年考研的同学赶不上这么简单的专业课啦&#xff01; 本套试卷难度分析&#xff1a;平均分为102和141分&a…
阅读更多...
一个悄然崛起的国产软件！！AI 又进化了！！

一个悄然崛起的国产软件！！AI 又进化了！！

大家好&#xff0c;我是 Jack。 AI 写代码想必很多人都体验过了&#xff0c;使用 AI 编程工具是一个大趋势&#xff0c;越早学会使用 AI 辅助你写代码&#xff0c;你的效率也会越高。 甚至有些公司已经要求员工具备 AI 编程能力。 对于学生党&#xff0c;AI 编程可以帮助我们…
阅读更多...
Android开发从0开始（广播）

Android开发从0开始（广播）

应用广播 发送标准广播的三步骤 发送标准广播&#xff1a; //发送标准广播 Intent intent new Intent("com.dongnaoedu.chapter09.standard"); sendBroadcast(intent); 定义广播接受者: public class StanderdReceiver extends BroadcastReceiver { public s…
阅读更多...
【腾讯云云上实验室-向量数据库】Tencent Cloud VectorDB为非结构化数据查询插上飞翔的翅膀——以企业知识库为例

【腾讯云云上实验室-向量数据库】Tencent Cloud VectorDB为非结构化数据查询插上飞翔的翅膀——以企业知识库为例

前言 以前我曾疑惑&#xff0c;对于非结构化的内容&#xff0c;如一张图片或一段视频&#xff0c;如何实现搜索呢&#xff1f;图片或视频作为二进制文件&#xff0c;我们如何将其转化为可搜索的数据并存储起来&#xff0c;然后在搜索时将其还原呢&#xff1f; 后来我发现&…
阅读更多...
关于进制的转化

关于进制的转化

二进制转十进制&#xff1a; &#x1f530; 方法一&#xff1a;二进制转十进制&#xff0c;用各数的码位与位权的乘积之和&#xff0c;说白了就是用从右到左的每个数去乘以2的幂次方&#xff08;最右边是0&#xff09;&#xff0c;然后就所有的数相加。 补充&#xff1a;位权是…
阅读更多...
【Mybatis】Mybatis操作数据库详解

【Mybatis】Mybatis操作数据库详解

Mybatis操作数据库 什么是MybatisMybatis入门准备工作创建Springboot工程 建表 创建实体类 配置数据库连接字符串编写持久层代码单元测试 Mybatis的基础操作打印日志参数传递增(insert)返回主键 删(delete)改(update)查(select) Mybatis XML配置文件配置连接字符串和Mybatis写持…
阅读更多...
虚拟化原理

虚拟化原理

目录 什么是虚拟化广义虚拟化狭义虚拟化 虚拟化指令集敏感指令集虚拟化指令集的工作模式监视器对敏感指令的处理过程&#xff1a; 虚拟化类型全虚拟化类虚拟化硬件辅助虚拟化 虚拟化架构裸金属架构宿主机模式架构 什么是虚拟化 虚拟化就是通过模仿下层原有的功能模块创造接口来…
阅读更多...
接口测试学习路线

接口测试学习路线

接口测试分为两种&#xff1a; 测试外部接口&#xff1a;系统和外部系统之间的接口 如&#xff1a;电商网站&#xff1a;支付宝支付 测试内部接口&#xff1a;系统内部的模块之间的联调&#xff0c;或者子系统之间的数据交互 测试重点&#xff1a;测试接口参数传递的正确性&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023