​

大纲

• 矩阵微积分：多元微积分的一种特殊表达，尤其是在矩阵空间上进行讨论的时候
• 逆矩阵(inverse matrix)
• 矩阵分解：特征分解（Eigendecomposition），又称谱分解（Spectral decomposition）；LU分解；奇异值分解（singular value decomposition）；QR分解；科列斯基分解
• 矩阵行列式（Determinant）：在欧几里得空间中，行列式描述的是一个线性变换对“体积”所造成的影响
• 特征向量（eigenvector）：$Av=\lambda v$，其中$\lambda$为特征值，$v$为$A$的特征向量，$A$的所有特征值的全体叫$A$的谱，记为$\lambda (A)$
• 迹（trance）：$\mathrm{tr}(\mathbf{A})={\mathbf{A}}_{1,1}+\cdots +{\mathbf{A}}_{n,n}$，一个矩阵的迹是其特征值的总和
• 正交矩阵（orthogonal matrix）：是一个方阵，其行向量與列向量皆為正交的单位向量，使得該矩陣的转置矩阵為其逆矩阵。$Q{Q}^T=I$
• 正定矩阵和半正定矩阵（positive semi-definite matrix）：一个 $n\times n$ 的实对称矩阵 $M$ 是正定的，当且仅当对于所有的非零实系数向量 $\mathbf{z}$，都有 ${\mathbf{z}}^{T}M\mathbf{z}>0$。其中 ${\mathbf{z}}^T$表示 $\mathbf{z}$ 的转置
• 伴随矩阵（adjugate matrix）：如果矩阵可逆，那么它的逆矩阵和它的伴随矩阵之间只差一个系数
• 共轭矩阵（又叫Hermite矩阵）：矩阵本身先转置再把矩阵中每个元素取共轭(虚部变号的运算)得到的矩阵
• 共轭转置（conjugate transpose or Hermitian transpose）：$A^{\ast }=(\overline{A}{)}^{\mathrm{T}}=\overline{A^{\mathrm{T}}}$, $\overline{A}$表示对矩阵A元素取复共轭
• 酉矩阵（又叫幺正矩阵，unitary matrix）：指其共轭转置恰为其逆矩阵的复数方阵，$U^{\ast }U=U{U}^{\ast }=I_n$
• 实对称矩阵：元素都为实数的对称矩阵
• 对角矩阵(diagonal matrix)：一个主对角线之外的元素皆为0的矩阵，常写为diag（a1，a2,…,an)
• 雅可比矩阵（Jacobian matrix）：$\mathbf{J}=\left[\begin{array}{ccc}\frac{\partial \mathbf{f}}{\partial x_1}& \cdots & \frac{\partial \mathbf{f}}{\partial x_n}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial f_1}{\partial x_1}& \cdots & \frac{\partial f_1}{\partial x_n}\\ ⋮& \ddots & ⋮\\ \frac{\partial f_m}{\partial x_1}& \cdots & \frac{\partial f_m}{\partial x_n}\end{array}\right]$
• 黑塞矩阵（又叫海森矩阵，Hessian matrix)：由多变量实值函数的所有二阶偏导数组成的方阵，${\mathbf{H}}_{ij}=\frac{{\partial }^{2}f}{\partial x_i\partial x_j}$
• 矩阵范数（matrix norm）

---

一、矩阵微积分

向量对向量的偏导称 Jacobian Matrix:
$$J=\frac{\partial y_{(n)}}{\partial x_{(m)}}={\left(\begin{array}{ccc}\frac{\partial y_1}{\partial x_1}& \cdots & \frac{\partial y_1}{\partial x_m}\\ ⋮& \ddots & ⋮\\ \frac{\partial y_n}{\partial x_1}& \cdots & \frac{\partial y_n}{\partial x_m}\end{array}\right)}_{n\times m}$$
标量对向量的偏导、向量对标量的偏导都是相应向量为一维的情况。
这里采用了称为分子布局的表示方法，另外还有将矩阵（向量）微积分表示为这里这种形式的转置的，称为分母布局。但用分母布局表示时，下面的运算法则没有这么好记的形式。

与标量微积分对比：

• 加法法则不变 $$\frac{\partial y+z}{\partial x}=\frac{\partial y}{\partial x}+\frac{\partial z}{\partial x}$$

• 链式法则不变 $$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\cdot \frac{\partial y}{\partial x}$$

• 乘法法则形式不变 $$\frac{\partial y\otimes z}{\partial x}=y\otimes \frac{\partial z}{\partial x}+z\otimes \frac{\partial y}{\partial x}$$

  • 向量内积 $$\frac{\partial y^{T}z}{\partial x}=y^T\cdot \frac{\partial z}{\partial x}+z^T\cdot \frac{\partial y}{\partial x}$$
  • 矩阵乘积（A 与 x 无关） $$\frac{\partial Ay}{\partial x}=A\cdot \frac{\partial y}{\partial x}$$
  • 向量数乘（y 或 z 为标量） $$\frac{\partial yz}{\partial x}=y\cdot \frac{\partial z}{\partial x}+z\cdot \frac{\partial y}{\partial x}$$

${\sum }_{i=1}^n{i}^2=\frac{n(n+1)(2n+1)}{6}$

1. 表示法

• $\mathbf{A},\mathbf{X},\mathbf{Y}$ 等：粗体的大写字母，表示一个矩阵
• $\mathbf{a},\mathbf{x},\mathbf{y}$ 等：粗体的小写字母，表示一个向量；
• $a,x,y$ 等：斜体的小写字母，表示一个标量；
• ${\mathbf{X}}^T$：表示矩阵 $\mathbf{X}$ 的转置；
• ${\mathbf{X}}^H$：表示矩阵 $\mathbf{X}$ 的共轭转置；
• $|\mathbf{X}|$：表示方阵 $\mathbf{X}$ 的行列式；
• $||\mathbf{x}||$：表示向量 $\mathbf{x}$ 的范数；
• $\mathbf{I}$：表示单位矩阵。

2. 向量微分

2.1 向量-标量

列向量函数 $\mathbf{y}={\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_m\end{array}\right]}^T$ 对标量 $x$ 的导数称为 $\mathbf{y}$ 的切向量，可以以 分子记法 表示为 $\frac{\partial \mathbf{y}}{\partial x}={\left[\begin{array}{c}\frac{\partial y_1}{\partial x}\\ \frac{\partial y_2}{\partial x}\\ ⋮\\ \frac{\partial y_m}{\partial x}\end{array}\right]}_{m\times 1}$

若以 分母记法 则可以表示为 $\frac{\partial \mathbf{y}}{\partial x}={\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x}& \frac{\partial y_2}{\partial x}& \cdots & \frac{\partial y_m}{\partial x}\end{array}\right]}_{1\times m}$

2.2 标量-向量

标量函数 $y$ 对列向量 $\mathbf{x}={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]}^T$ 的导数可以以 分子记法 表示为 $\frac{\partial y}{\partial \mathbf{x}}={\left[\begin{array}{cccc}\frac{\partial y}{\partial x_1}& \frac{\partial y}{\partial x_2}& \cdots & \frac{\partial y}{\partial x_n}\end{array}\right]}_{1\times n}$

若以 分母记法 则可以表示为 $\frac{\partial y}{\partial \mathbf{x}}={\left[\begin{array}{c}\frac{\partial y}{\partial x_1}\\ \frac{\partial y}{\partial x_2}\\ ⋮\\ \frac{\partial y}{\partial x_n}\end{array}\right]}_{n\times 1}$

2.3 向量-向量

列向量函数 $\mathbf{y}={\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_m\end{array}\right]}^T$ 对列向量 $\mathbf{x}={\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]}^T$ 的导数可以以 分子记法 表示为
$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}={\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \cdots & \frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}& \cdots & \frac{\partial y_2}{\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_m}{\partial x_1}& \frac{\partial y_m}{\partial x_2}& \cdots & \frac{\partial y_m}{\partial x_n}\end{array}\right]}_{m\times n}$

若以 分母记法 则可以表示为
$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}={\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_1}\\ \frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_1}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \cdots & \frac{\partial y_m}{\partial x_1}\end{array}\right]}_{n\times m}$

3. 矩阵微分

1. 矩阵-标量

形状为 $m\times n$ 的矩阵函数 $\mathbf{Y}$ 对标量 $x$ 的导数称为 $\mathbf{Y}$ 的切矩阵，可以以 分子记法 表示为
$\frac{\partial \mathbf{Y}}{\partial x}={\left[\begin{array}{cccc}\frac{\partial y_{11}}{\partial x}& \frac{\partial y_{12}}{\partial x}& \cdots & \frac{\partial y_{1n}}{\partial x}\\ \frac{\partial y_{21}}{\partial x}& \frac{\partial y_{22}}{\partial x}& \cdots & \frac{\partial y_{2n}}{\partial x}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_{m1}}{\partial x}& \frac{\partial y_{m2}}{\partial x}& \cdots & \frac{\partial y_{mn}}{\partial x}\end{array}\right]}_{m\times n}$

2. 标量-矩阵

标量函数 $y$ 对形状为 $p\times q$ 的矩阵 $\mathbf{X}$ 的导数可以 分子记法 表示为

$\frac{\partial y}{\partial \mathbf{X}}={\left[\begin{array}{cccc}\frac{\partial y}{\partial x_{11}}& \frac{\partial y}{\partial x_{21}}& \cdots & \frac{\partial y}{\partial x_{p1}}\\ \frac{\partial y}{\partial x_{12}}& \frac{\partial y}{\partial x_{22}}& \cdots & \frac{\partial y}{\partial x_{p2}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y}{\partial x_{1q}}& \frac{\partial y}{\partial x_{2q}}& \cdots & \frac{\partial y}{\partial x_{pq}}\end{array}\right]}_{q\times p}$
若以 分母记法 则可以表示为
$\frac{\partial y}{\partial \mathbf{X}}={\left[\begin{array}{cccc}\frac{\partial y}{\partial x_{11}}& \frac{\partial y}{\partial x_{12}}& \cdots & \frac{\partial y}{\partial x_{1q}}\\ \frac{\partial y}{\partial x_{21}}& \frac{\partial y}{\partial x_{22}}& \cdots & \frac{\partial y}{\partial x_{2q}}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y}{\partial x_{p1}}& \frac{\partial y}{\partial x_{p2}}& \cdots & \frac{\partial y}{\partial x_{pq}}\end{array}\right]}_{p\times q}$

4. 恒等式

以下各式中，无特别备注，默认被求导的复合函数的各因式皆不是求导变量的函数。

4.1. 向量-向量

表达式	分子记法	分母记法	备注
$\frac{\partial \mathbf{a}}{\partial \mathbf{x}}=$	$0$	$0$
$\frac{\partial \mathbf{x}}{\partial \mathbf{x}}=$	$\mathbf{I}$	$\mathbf{I}$
$\frac{\partial \mathbf{Ax}}{\partial \mathbf{x}}=$	$\mathbf{A}$	${\mathbf{A}}^T$
$\frac{\partial {\mathbf{x}}^T\mathbf{A}}{\partial \mathbf{x}}=$	${\mathbf{A}}^T$	$\mathbf{A}$
$\frac{\partial a\mathbf{u}}{\partial \mathbf{x}}=$	$a\frac{\partial \mathbf{u}}{\partial x}$	$a\frac{\partial \mathbf{u}}{\partial x}$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial v\mathbf{u}}{\partial \mathbf{x}}=$	$v\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\mathbf{u}\frac{\partial v}{\partial \mathbf{x}}$	$v\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{\partial v}{\partial \mathbf{x}}{\mathbf{u}}^T$	$v=v(\mathbf{x}),\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial \mathbf{Au}}{\partial \mathbf{x}}=$	$\mathbf{A}\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{u}}{\partial \mathbf{x}}{\mathbf{A}}^T$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial (\mathbf{u}+\mathbf{v})}{\partial \mathbf{x}}=$	$\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{\partial \mathbf{v}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{\partial \mathbf{v}}{\partial \mathbf{x}}$	$\mathbf{u}=\mathbf{u}(\mathbf{x}),\mathbf{v}=\mathbf{v}(\mathbf{x})$
$\frac{\partial \mathbf{f}(\mathbf{g}(\mathbf{u}))}{\partial \mathbf{x}}=$	$\frac{\partial \mathbf{f}(\mathbf{g})}{\partial \mathbf{g}}\frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{u}}\frac{\partial \mathbf{f}(\mathbf{g})}{\partial \mathbf{g}}$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$

4.2. 标量-向量

表达式	分子记法	分母记法	备注
$\frac{\partial a}{\partial \mathbf{x}}=$	$0^T$	$0$
$\frac{\partial au}{\partial \mathbf{x}}=$	$a\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$a\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$u=u(\mathbf{x})$
$\frac{\partial (u+v)}{\partial \mathbf{x}}=$	$\frac{\partial u}{\partial \mathbf{x}}+\frac{\partial v}{\partial \mathbf{x}}$	$\frac{\partial u}{\partial \mathbf{x}}+\frac{\partial v}{\partial \mathbf{x}}$	$u=u(\mathbf{x}),v=v(\mathbf{x})$
$\frac{\partial uv}{\partial \mathbf{x}}=$	$u\frac{\partial v}{\partial \mathbf{x}}+v\frac{\partial u}{\partial \mathbf{x}}$	$u\frac{\partial v}{\partial \mathbf{x}}+v\frac{\partial u}{\partial \mathbf{x}}$	$u=u(\mathbf{x}),v=v(\mathbf{x})$
$\frac{\partial f(g(u))}{\partial \mathbf{x}}=$	$\frac{\partial f(g)}{\partial g}\frac{\partial g(u)}{\partial u}\frac{\partial u}{\partial \mathbf{x}}$	$\frac{\partial f(g)}{\partial g}\frac{\partial g(u)}{\partial u}\frac{\partial u}{\partial \mathbf{x}}$	$u=u(\mathbf{x})$
$\frac{\partial (\mathbf{u}\cdot \mathbf{v})}{\partial \mathbf{x}}=\frac{\partial {\mathbf{u}}^T\mathbf{v}}{\partial \mathbf{x}}=$	${\mathbf{u}}^T\frac{\partial \mathbf{v}}{\partial \mathbf{x}}+{\mathbf{v}}^T\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{v}}{\partial \mathbf{x}}\mathbf{u}+\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\mathbf{v}$	$\mathbf{u}=\mathbf{u}(\mathbf{x}),\mathbf{v}=\mathbf{v}(\mathbf{x})$
$\frac{\partial (\mathbf{u}\cdot \mathbf{Av})}{\partial \mathbf{x}}=\frac{\partial {\mathbf{u}}^T\mathbf{Av}}{\partial \mathbf{x}}=$	${\mathbf{u}}^T\mathbf{A}\frac{\partial \mathbf{v}}{\partial \mathbf{x}}+{\mathbf{v}}^T{\mathbf{A}}^T\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{v}}{\partial \mathbf{x}}{\mathbf{A}}^T\mathbf{u}+\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\mathbf{Av}$	$\mathbf{u}=\mathbf{u}(\mathbf{x}),\mathbf{v}=\mathbf{v}(\mathbf{x})$
$\frac{\partial (\mathbf{a}\cdot \mathbf{u})}{\partial \mathbf{x}}=\frac{\partial {\mathbf{a}}^T\mathbf{u}}{\partial \mathbf{x}}=$	${\mathbf{a}}^T\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\mathbf{a}$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial {\mathbf{b}}^T\mathbf{Ax}}{\partial \mathbf{x}}=$	${\mathbf{b}}^T\mathbf{A}$	${\mathbf{A}}^T\mathbf{b}$
$\frac{\partial {\mathbf{x}}^T\mathbf{Ax}}{\partial \mathbf{x}}=$	${\mathbf{x}}^T(\mathbf{A}+{\mathbf{A}}^T)$	$(\mathbf{A}+{\mathbf{A}}^T)\mathbf{x}$
$\frac{{\partial }^2{\mathbf{x}}^T\mathbf{Ax}}{\partial \mathbf{x}\partial {\mathbf{x}}^T}=$	$\mathbf{A}+{\mathbf{A}}^T$	$\mathbf{A}+{\mathbf{A}}^T$
$\frac{\partial {\mathbf{a}}^T\mathbf{x}{\mathbf{x}}^T\mathbf{b}}{\partial \mathbf{x}}=$	${\mathbf{x}}^T(\mathbf{a}{\mathbf{b}}^T+\mathbf{b}{\mathbf{a}}^T)$	$(\mathbf{a}{\mathbf{b}}^T+\mathbf{b}{\mathbf{a}}^T)\mathbf{x}$
$\frac{\partial (\mathbf{Ax}+\mathbf{b}{)}^T\mathbf{C}(\mathbf{Dx}+\mathbf{e})}{\partial \mathbf{x}}=$	$(\mathbf{Ax}+\mathbf{b}{)}^T\mathbf{CD}+(\mathbf{Dx}+\mathbf{e}{)}^T{\mathbf{C}}^T\mathbf{A}$	${\mathbf{D}}^T{\mathbf{C}}^T(\mathbf{Ax}+\mathbf{b})+{\mathbf{A}}^T\mathbf{C}(\mathbf{Dx}+\mathbf{e}{)}^T$
$\frac{\partial ||\mathbf{x}|{|}^2}{\partial \mathbf{x}}=\frac{\partial (\mathbf{x}\cdot \mathbf{x})}{\partial \mathbf{x}}=$	$2{\mathbf{x}}^T$	$2\mathbf{x}$
$\frac{\partial ||\mathbf{x}-\mathbf{a}||}{\partial \mathbf{x}}=$	$\frac{(\mathbf{x}-\mathbf{a}{)}^T}{||\mathbf{x}-\mathbf{a}||}$	$\frac{(\mathbf{x}-\mathbf{a})}{||\mathbf{x}-\mathbf{a}||}$

4.3. 向量-标量

表达式	分子记法	分母记法	备注
$\frac{\partial \mathbf{a}}{\partial x}=$	$0$	$0$
$\frac{\partial a\mathbf{u}}{\partial x}=$	$a\frac{\partial \mathbf{u}}{\partial x}$	$a\frac{\partial \mathbf{u}}{\partial x}$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial \mathbf{Au}}{\partial x}=$	$\mathbf{A}\frac{\partial \mathbf{u}}{\partial x}$	$\frac{\partial \mathbf{u}}{\partial x}{\mathbf{A}}^T$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial {\mathbf{u}}^T}{\partial x}=$	${\left(\frac{\partial \mathbf{u}}{\partial x}\right)}^T$	${\left(\frac{\partial \mathbf{u}}{\partial x}\right)}^T$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial (\mathbf{u}+\mathbf{v})}{\partial x}=$	$\frac{\partial \mathbf{u}}{\partial x}+\frac{\partial \mathbf{v}}{\partial x}$	$\frac{\partial \mathbf{u}}{\partial x}+\frac{\partial \mathbf{v}}{\partial x}$	$\mathbf{u}=\mathbf{u}(\mathbf{x}),\mathbf{v}=\mathbf{v}(\mathbf{x})$
$\frac{\partial ({\mathbf{u}}^T\times \mathbf{v})}{\partial x}=$	${\left(\frac{\partial \mathbf{u}}{\partial x}\right)}^T\times \mathbf{v}+{\mathbf{u}}^T\times \frac{\partial \mathbf{v}}{\partial x}$	$\frac{\partial \mathbf{u}}{\partial x}\times \mathbf{v}+{\mathbf{u}}^T\times {\left(\frac{\partial \mathbf{v}}{\partial x}\right)}^T$	$\mathbf{u}=\mathbf{u}(\mathbf{x}),\mathbf{v}=\mathbf{v}(\mathbf{x})$
$\frac{\partial \mathbf{f}(\mathbf{g}(\mathbf{u}))}{\partial x}=$	$\frac{\partial \mathbf{f}(\mathbf{g})}{\partial \mathbf{g}}\frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial x}$	$\frac{\partial \mathbf{u}}{\partial x}\frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{u}}\frac{\partial \mathbf{f}(\mathbf{g})}{\partial \mathbf{g}}$	$\mathbf{u}=\mathbf{u}(\mathbf{x})$
$\frac{\partial (\mathbf{U}\times \mathbf{v})}{\partial x}=$	$\frac{\partial \mathbf{U}}{\partial x}\times \mathbf{v}+\mathbf{U}\times \frac{\partial \mathbf{v}}{\partial x}$	${\mathbf{v}}^T\times \frac{\partial \mathbf{U}}{\partial x}+\frac{\partial \mathbf{v}}{\partial x}\times {\mathbf{U}}^T$	$\mathbf{U}=\mathbf{U}(\mathbf{x}),\mathbf{v}=\mathbf{v}(\mathbf{x})$

4.4. 标量-矩阵

表达式	分子记法	分母记法	备注
$\frac{\partial a}{\partial \mathbf{X}}=$	$0^T$	$0$
$\frac{\partial au}{\partial \mathbf{X}}=$	$a\frac{\partial u}{\partial \mathbf{X}}$	$a\frac{\partial u}{\partial \mathbf{X}}$	$u=u(\mathbf{X})$
$\frac{\partial (u+v)}{\partial \mathbf{X}}=$	$\frac{\partial u}{\partial \mathbf{X}}+\frac{\partial v}{\partial \mathbf{X}}$	$\frac{\partial u}{\partial \mathbf{X}}+\frac{\partial v}{\partial \mathbf{X}}$	$u=u(\mathbf{X}),v=v(\mathbf{X})$
$\frac{\partial uv}{\partial \mathbf{X}}=$	$u\frac{\partial v}{\partial \mathbf{X}}+v\frac{\partial u}{\partial \mathbf{X}}$	$u\frac{\partial v}{\partial \mathbf{X}}+v\frac{\partial u}{\partial \mathbf{X}}$	$u=u(\mathbf{X}),v=v(\mathbf{X})$
$\frac{\partial f(g(u))}{\partial \mathbf{X}}=$	$\frac{\partial f(g)}{\partial g}\frac{\partial g(u)}{\partial u}\frac{\partial u}{\partial \mathbf{X}}$	$\frac{\partial f(g)}{\partial g}\frac{\partial g(u)}{\partial u}\frac{\partial u}{\partial \mathbf{X}}$	$u=u(\mathbf{X})$
$\frac{\partial {\mathbf{a}}^T\mathbf{Xb}}{\partial \mathbf{X}}=$	$\mathbf{b}{\mathbf{a}}^T$	$\mathbf{a}{\mathbf{b}}^T$
$\frac{\partial {\mathbf{a}}^T{\mathbf{X}}^T\mathbf{b}}{\partial \mathbf{X}}=$	$\mathbf{a}{\mathbf{b}}^T$	$\mathbf{b}{\mathbf{a}}^T$
$\frac{\partial (\mathbf{Xa}+\mathbf{b}{)}^T\mathbf{C}(\mathbf{Xa}+\mathbf{b})}{\partial \mathbf{X}}=$	$[(\mathbf{C}+{\mathbf{C}}^T)(\mathbf{Xa}+\mathbf{b}){\mathbf{a}}^T{]}^T$	$(\mathbf{C}+{\mathbf{C}}^T)(\mathbf{Xa}+\mathbf{b}){\mathbf{a}}^T$
$\frac{\partial (\mathbf{Xa}{)}^T\mathbf{C}(\mathbf{Xb})}{\partial \mathbf{X}}=$	$(\mathbf{CXb}{\mathbf{a}}^T+{\mathbf{C}}^T\mathbf{Xa}{\mathbf{b}}^T{)}^T$	$\mathbf{CXb}{\mathbf{a}}^T+{\mathbf{C}}^T\mathbf{Xa}{\mathbf{b}}^T$
$\frac{\partial |\mathbf{X}|}{\partial \mathbf{X}}=$	$|\mathbf{X}|{\mathbf{X}}^{-1}$	$|\mathbf{X}|({\mathbf{X}}^{-1}{)}^T$
$\frac{\partial \ln |a\mathbf{X}|}{\partial \mathbf{X}}=$	${\mathbf{X}}^{-1}$	$({\mathbf{X}}^{-1}{)}^T$
$\frac{\partial |\mathbf{AXB}|}{\partial \mathbf{X}}=$	$|\mathbf{AXB}|{\mathbf{X}}^{-1}$	$|\mathbf{AXB}|({\mathbf{X}}^{-1}{)}^T$
$\frac{\partial |{\mathbf{X}}^n|}{\partial \mathbf{X}}=$	$n|{\mathbf{X}}^n|{\mathbf{X}}^{-1}$	$n|{\mathbf{X}}^n|({\mathbf{X}}^{-1}{)}^T$
$\frac{\partial \ln |{\mathbf{X}}^T\mathbf{X}|}{\partial \mathbf{X}}=$	$2{\mathbf{X}}^{+}$	$2({\mathbf{X}}^{+}{)}^T$	${\mathbf{X}}^{+}$ 为 $\mathbf{X}$ 的广义逆
$\frac{\partial \ln |{\mathbf{X}}^T\mathbf{X}|}{\partial {\mathbf{X}}^{+}}=$	$-2\mathbf{X}$	$-2{\mathbf{X}}^T$	${\mathbf{X}}^{+}$ 为 $\mathbf{X}$ 的广义逆
$\frac{\partial |{\mathbf{X}}^T\mathbf{AX}|}{\partial \mathbf{X}}=$	$2|{\mathbf{X}}^T\mathbf{AX}|{\mathbf{X}}^{-1}=2|{\mathbf{X}}^T||\mathbf{A}||\mathbf{X}|{\mathbf{X}}^{-1}$	$2|{\mathbf{X}}^T\mathbf{AX}|({\mathbf{X}}^{-1}{)}^T$	$\mathbf{X}$ 为方阵且可逆
$\frac{\partial |{\mathbf{X}}^T\mathbf{AX}|}{\partial \mathbf{X}}=$	$2|{\mathbf{X}}^T\mathbf{AX}|({\mathbf{X}}^T{\mathbf{A}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T{\mathbf{A}}^T$	$2|{\mathbf{X}}^T\mathbf{AX}|\mathbf{AX}({\mathbf{X}}^T\mathbf{AX}{)}^{-1}$	$\mathbf{A}$ 对称
$\frac{\partial |{\mathbf{X}}^T\mathbf{AX}|}{\partial \mathbf{X}}=$	$|{\mathbf{X}}^T\mathbf{AX}|[({\mathbf{X}}^T\mathbf{AX}{)}^{-1}{\mathbf{X}}^T\mathbf{A}+({\mathbf{X}}^T{\mathbf{A}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T{\mathbf{A}}^T]$	$|{\mathbf{X}}^T\mathbf{AX}|[\mathbf{AX}({\mathbf{X}}^T\mathbf{AX}{)}^{-1}+{\mathbf{A}}^T\mathbf{X}({\mathbf{X}}^T{\mathbf{A}}^T\mathbf{X}{)}^{-1}]$

4.5. 矩阵-标量

表达式	分子记法	备注
$\frac{\partial a\mathbf{U}}{\partial x}=$	$a\frac{\partial \mathbf{U}}{\partial x}$	$\mathbf{U}=\mathbf{U}(x)$
$\frac{\partial \mathbf{AUB}}{\partial x}=$	$\mathbf{A}\frac{\partial \mathbf{U}}{\partial x}\mathbf{B}$	$\mathbf{U}=\mathbf{U}(x)$
$\frac{\partial (\mathbf{U}+\mathbf{V})}{\partial x}=$	$\frac{\partial \mathbf{U}}{\partial x}+\frac{\partial \mathbf{V}}{\partial x}$	$\mathbf{U}=\mathbf{U}(x),\mathbf{V}=\mathbf{V}(x)$
$\frac{\partial (\mathbf{UV})}{\partial x}=$	$\mathbf{U}\frac{\partial \mathbf{V}}{\partial x}+\frac{\partial \mathbf{U}}{\partial x}\mathbf{V}$	$\mathbf{U}=\mathbf{U}(x),\mathbf{V}=\mathbf{V}(x)$
$\frac{\partial (\mathbf{U}\otimes \mathbf{V})}{\partial x}=$	$\mathbf{U}\otimes \frac{\partial \mathbf{V}}{\partial x}+\frac{\partial \mathbf{U}}{\partial x}\otimes \mathbf{V}$	$\mathbf{U}=\mathbf{U}(x),\mathbf{V}=\mathbf{V}(x)$；$\otimes$ 表示 Kronecker 乘积
$\frac{\partial (\mathbf{U}\circ \mathbf{V})}{\partial x}=$	$\mathbf{U}\circ \frac{\partial \mathbf{V}}{\partial x}+\frac{\partial U}{\partial x}\circ \mathbf{V}$	$\mathbf{U}=\mathbf{U}(x),\mathbf{V}=\mathbf{V}(x)$；$\circ$ 表示 Hadamard 乘积
$\frac{\partial {\mathbf{U}}^{-1}}{\partial x}=$	$-{\mathbf{U}}^{-1}\frac{\partial \mathbf{U}}{\partial x}{\mathbf{U}}^{-1}$	$\mathbf{U}=\mathbf{U}(x)$
$\frac{{\partial }^2{\mathbf{U}}^{-1}}{\partial x\partial y}=$	${\mathbf{U}}^{-1}\left(\frac{\partial \mathbf{U}}{\partial x}{\mathbf{U}}^{-1}\frac{\partial \mathbf{U}}{\partial y}-\frac{{\partial }^2\mathbf{U}}{\partial x\partial y}+\frac{\partial \mathbf{U}}{\partial y}{\mathbf{U}}^{-1}\frac{\partial \mathbf{U}}{\partial x}\right){\mathbf{U}}^{-1}$	$\mathbf{U}=\mathbf{U}(x,y)$
$\frac{\partial g(x\mathbf{A})}{\partial x}=$	$\mathbf{A}{g}^{\prime }(x\mathbf{A})=g^{\prime }(x\mathbf{A})\mathbf{A}$	应为 Hadamard 乘积；$g(\cdot )$ 为逐元函数，如下例
$\frac{\partial e^{x\mathbf{A}}}{\partial x}=$	$\mathbf{A}{e}^{x\mathbf{A}}=e^{x\mathbf{A}}\mathbf{A}$

二、矩阵分解

• QR分解：$M=QR$, Q正交，R上三角。
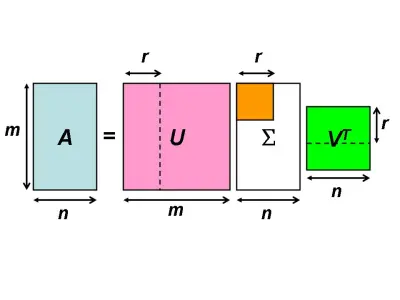
• 奇异值分解（Singular Value Decomposition，SVD）：$M=U\Sigma V^T$, U和V正交，Σ非负对角。
• 特征分解（Eigendecomposition）,又叫谱分解(Spectral decomposition)：$S=Q\Lambda Q^T$, S对称，Q正交，Λ对角。
• 极分解：$M=QS$, Q正交，S对称半正定。
• 科列斯基分解（Cholesky decomposition）：$\mathbf{A}={\mathbf{LL}}^{\ast }$，$\mathbf{L}$ 下三角矩阵且所有对角元素均为正实数，${\mathbf{L}}^{\ast }$表示 $\mathbf{L}$ 的共轭转置。每一个正定埃尔米特矩阵都有一个唯一的科列斯基分解
• LU分解：$A=LU$，L下三角, U上三角

1. 科列斯基分解

科列斯基分解主要被用于线性方程组 $\mathbf{Ax}=\mathbf{b}$ 的求解。如果 $A$ 是对称正定的，我们可以先求出$\mathbf{A}={\mathbf{LL}}^{\mathbf{T}}$，随后借向后替换法对 $y$ 求解$\mathbf{Ly}=\mathbf{b}$，再以向前替换法对 $x$ 求解${\mathbf{L}}^{\mathbf{T}}\mathbf{x}=\mathbf{y}$即得最终解。
另一种可避免在计算${\mathbf{LL}}^{\mathbf{T}}$时需要解平方根的方法就是计算 $\mathbf{A}={\mathbf{LDL}}^{\mathrm{T}}$，然后对 $y$ 求解 $\mathbf{Ly}=\mathbf{b}$，最后求解${\mathbf{DL}}^{\mathrm{T}}\mathbf{x}=\mathbf{y}$
对于可以被改写成对称矩阵的线性方程组，科列斯基分解及其LDL变形是一个较高效率及较高数值稳定性的求解方法。相比之下，其效率几近为LU分解的两倍

2. SGD分解

三、矩阵种类

1.「正定矩阵」和「半正定矩阵」

案例：多元正态分布的协方差矩阵要求是半正定的

【定义1】 给定一个大小为 $n\times n$ 的实对称矩阵 $A$，若对于任意长度为 $n$ 的非零向量$\mathbf{x}$，有 ${\mathbf{x}}^{T}A\mathbf{x}>0$ 恒成立，则矩阵 $A$是一个正定矩阵。

【定义2】 给定一个大小为 $n\times n$ 的实对称矩阵 $A$ ，若对于任意长度为 $n$ 的向量 $\mathbf{x}$ ，有 ${\mathbf{x}}^{T}A\mathbf{x}\ge 0$ 恒成立，则矩阵 $A$ 是一个半正定矩阵。

直观解释：
若给定任意一个正定矩阵 $A\in {\mathbb{R}}^{n\times n}$ 和一个非零向量 $\mathbf{x}\in {\mathbb{R}}^n$ ，则两者相乘得到的向量 $\mathbf{y}=A\mathbf{x}\in {\mathbb{R}}^n$ 与向量 $\mathbf{x}$ 的夹角恒小于 $\frac{\pi }{2}$ . (等价于： ${\mathbf{x}}^{T}A\mathbf{x}>0$ .)
若给定任意一个半正定矩阵 $A\in {\mathbb{R}}^{n\times n}$ 和一个向量 $\mathbf{x}\in {\mathbb{R}}^n$ ，则两者相乘得到的向量 $\mathbf{y}=A\mathbf{x}\in {\mathbb{R}}^n$ 与向量 $\mathbf{x}$ 的夹角恒小于或等于 $\frac{\pi }{2}$ . (等价于： ${\mathbf{x}}^{T}A\mathbf{x}\ge 0$ .)

1.1 为什么协方差矩阵是半正定的

对于任意多元随机变量 $\mathbf{t}$ ，协方差矩阵为
$C=\mathbb{E}\left[(\mathbf{t}-\bar{\mathbf{t}})(\mathbf{t}-\bar{\mathbf{t}}{)}^T\right]$

现给定任意一个向量 $\mathbf{x}$ ，则 $${\mathbf{x}}^{T}C\mathbf{x}={\mathbf{x}}^T\mathbb{E}\left[(\mathbf{t}-\bar{\mathbf{t}})(\mathbf{t}-\bar{\mathbf{t}}{)}^T\right]\mathbf{x}=\mathbb{E}\left[{\mathbf{x}}^T(\mathbf{t}-\bar{\mathbf{t}})(\mathbf{t}-\bar{\mathbf{t}}{)}^T\mathbf{x}\right]=\mathbb{E}(s^2)={\sigma }_s^2$$
其中，${\sigma }_s={\mathbf{x}}^T(\mathbf{t}-\bar{\mathbf{t}})=(\mathbf{t}-\bar{\mathbf{t}}{)}^T\mathbf{x}$。由于 ${\sigma }_s^2\ge 0$ ，因此，${\mathbf{x}}^{T}C\mathbf{x}\ge 0$ ，协方差矩阵 $C$ 是半正定的。

2. 逆矩阵

分块矩阵（Block matrix） 的逆矩阵恒等式：
${\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)}^{-1}=\left(\begin{array}{cc}M& -MB{D}^{-1}\\ -D^{-1}CM& D^{-1}+D^{-1}CMB{D}^{-1}\end{array}\right)$
其中$M=(A-B{D}^{-1}C{)}^{-1}$

若A,C为可逆方阵，则有 $(A+BCD{)}^{-1}=A^{-1}-A^{-1}B(D{A}^{-1}B+C^{-1}{)}^{-1}D{A}^{-1}$

---

工具网站

• Matrix Calculus：在线计算矩阵导数

References

矩阵微积分 | Here4U