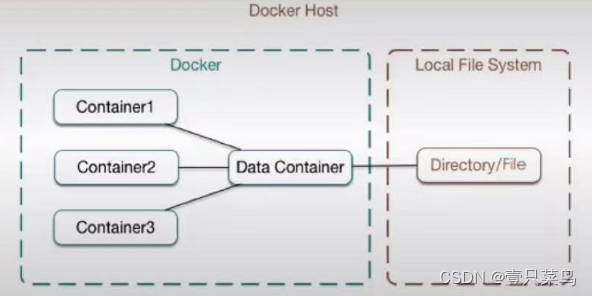
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
题目:给定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,求它们能排成的所有序列中,能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个?
输出的答案对 1 0 9 + 7 10^9+7 109+7取模。
原题目等价于,
在平面直角坐标系xoy下,起点为(0,0),终点为(n,n),每次只能向上走一格或向右走一格,问从起点走到终点,且路径上横坐标大于等于纵坐标恒成立,求有多少种走法?
用下图表示即为,
在不触碰到红线(即 y = x + 1 y=x+1 y=x+1)的情况下,从起点(0,0)走到终点(n,n),有多少种走法。

考虑一种触碰到红线,走到终点(n,n)的路径,如下图粗蓝色所显示路径。我们将从首次触碰到红线的点,记作红点。那么,将接下来的路径按照红线( y = x + 1 y=x+1 y=x+1)对称,可以得到粗绿色所显示路径,最终走到点(n-1,n+1)。

也就是说,任何一条触碰红线,走到终点(n,n)的路径,都可以等效成,一条走到(n-1,n+1)的路径。而从起点走到点(n-1,n+1)的路径数为 C 2 n n − 1 C_{2n}^{n-1} C2nn−1,故触碰红线走到终点的路径数目为 C 2 n n − 1 C_{2n}^{n-1} C2nn−1。
题目要计算的是,不触碰红线走到终点(n,n)的路径数目,它等于总路径数目减去触碰红线走到终点(n,n)的路径数目,即答案可计算如下,
C 2 n n − C 2 n n − 1 = ( 2 n ) ! n ! ⋅ n ! − ( 2 n ) ! ( n − 1 ) ! ⋅ ( n + 1 ) ! C_{2n}^n-C_{2n}^{n-1}=\frac{(2n)!}{n!\cdot n!} - \frac{(2n)!}{(n-1)!\cdot (n+1)!} C2nn−C2nn−1=n!⋅n!(2n)!−(n−1)!⋅(n+1)!(2n)!
= ( 2 n ) ! ( n − 1 ) ! ⋅ n ! ⋅ ( 1 n − 1 n + 1 ) = ( 2 n ) ! ( n − 1 ) ! ⋅ n ! ⋅ 1 n ( n + 1 ) =\frac{(2n)!}{(n-1)!\cdot n!}\cdot (\frac{1}{n} - \frac{1}{n+1})=\frac{(2n)!}{(n-1)!\cdot n!}\cdot \frac{1}{n(n+1)} =(n−1)!⋅n!(2n)!⋅(n1−n+11)=(n−1)!⋅n!(2n)!⋅n(n+1)1
= ( 2 n ) ! n ! ⋅ n ! ⋅ 1 n + 1 = C 2 n n n + 1 =\frac{(2n)!}{n!\cdot n!} \cdot \frac{1}{n+1}=\frac{C_{2n}^n}{n+1} =n!⋅n!(2n)!⋅n+11=n+1C2nn
其中 C 2 n n n + 1 \frac{C_{2n}^{n}}{n+1} n+1C2nn即为卡特兰数。
转换为代码,如下,
#include <iostream>using namespace std;const int mod = 1e9 + 7;int qmi(int a, int k, int p) {int res = 1;while (k) {if (k & 1) res = (long long)res * a % p;k >>= 1;a = (long long)a * a % p;}return res;
}int main() {int n;cin >> n;//计算C[2 * n][n] / (n + 1) % modint res = 1;for (int i = 1, j = 2 * n; i <= n; ++i, --j) {res = (long long)res * j % mod;res = (long long)res * qmi(i, mod - 2, mod) % mod;} res = (long long)res * qmi(n + 1, mod - 2, mod) % mod;cout << res << endl;return 0;
}
2 模板
暂无。。。
3 工程化
暂无。。。


![C++初阶 | [六] 模板初阶](https://img-blog.csdnimg.cn/464b9ae5866c4345b3c43c86f3d649f5.png)