目录链接:
力扣编程题-解法汇总_分享+记录-CSDN博客
GitHub同步刷题项目:
https://github.com/September26/java-algorithms
原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
描述:
给你一个下标从 0 开始的整数矩阵 grid ,矩阵大小为 m x n ,由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中,从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ,且满足 x < m - 1 ,你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意: 在最后一行中的单元格不能触发移动。
每次可能的移动都需要付出对应的代价,代价用一个下标从 0 开始的二维数组 moveCost 表示,该数组大小为 (m * n) x n ,其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发,返回到达 最后一行 任意单元格的最小路径代价。
示例 1:
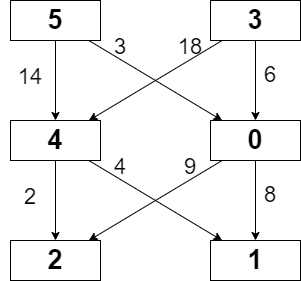
输入:grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]] 输出:17 解释:最小代价的路径是 5 -> 0 -> 1 。 - 路径途经单元格值之和 5 + 0 + 1 = 6 。 - 从 5 移动到 0 的代价为 3 。 - 从 0 移动到 1 的代价为 8 。 路径总代价为 6 + 3 + 8 = 17 。
示例 2:
输入:grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]] 输出:6 解释: 最小代价的路径是 2 -> 3 。 - 路径途经单元格值之和 2 + 3 = 5 。 - 从 2 移动到 3 的代价为 1 。 路径总代价为 5 + 1 = 6 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 50grid由从0到m * n - 1的不同整数组成moveCost.length == m * nmoveCost[i].length == n1 <= moveCost[i][j] <= 100
解题思路:
这是一道很经典的动态规划的题目。首先我们构建一个dp数组,dp[i]代表到达第i个结点时最小路径代价。然后我们可以逐行的求值,第一行直接使用其值即可。求第二行每个位置最小路径代价时,则遍历第一行所有可能性,求到grid[1][0]所对应位置的最小值即可。
以实例1举例,grid[1][0]=4,到4这个位置最小路径有两种可能性,5+14+4=23和3+18+4=25,则最小路径为23。同理,grid[2][0]=2时,也分别尝试使用grid[1][0]和grid[1][1]两个位置求到grid[2][0]的最小路经。
最后输出最后一行的路径最小值即可。
代码:
class Solution {
public:int minPathCost(vector<vector<int>> &grid, vector<vector<int>> &moveCost){vector<int> dp(grid.size() * grid[0].size());int minPath = 10000;for (int y = 0; y < grid.size(); y++){for (int x = 0; x < grid[y].size(); x++){int value = grid[y][x];if (y == 0){dp[value] = value;continue;}int minValue = 10000;for (int k = 0; k < grid[y - 1].size(); k++){int lastValue = grid[y - 1][k];minValue = min(minValue, dp[lastValue] + moveCost[lastValue][x]);}dp[value] = minValue + value;if (y == grid.size() - 1){minPath = min(minPath, dp[value]);}}}return minPath;}
};