springboot 返回problem+json-编程知识

springboot 返回problem+json

news/2024/9/26 2:03:55/文章来源:https://blog.csdn.net/qq_41170818/article/details/134609138

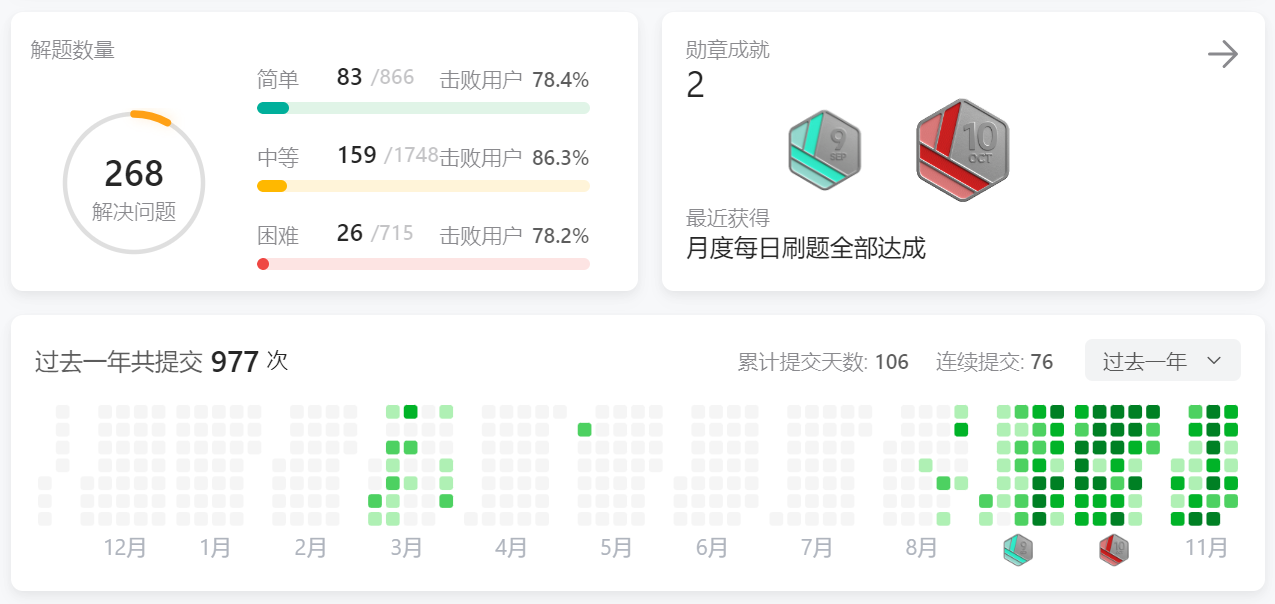
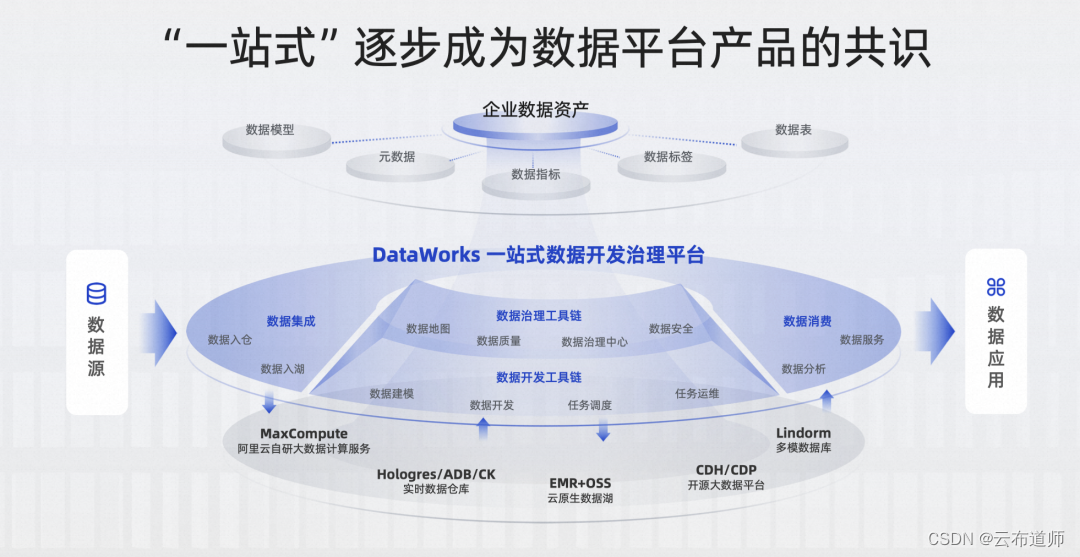
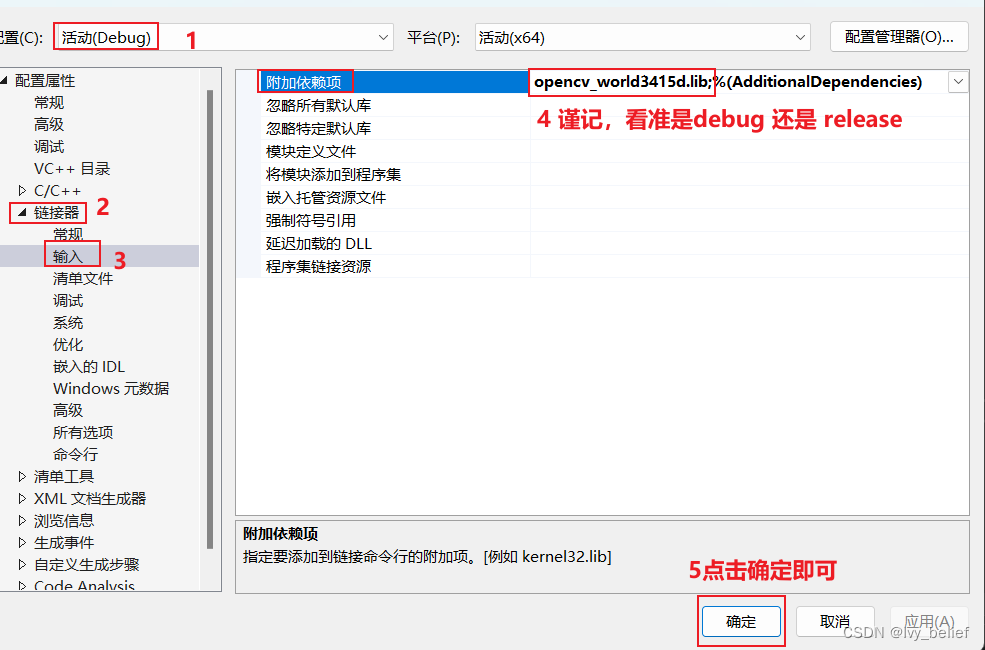
spring所有配置都在WebMvcAutoConfiguration中

其中有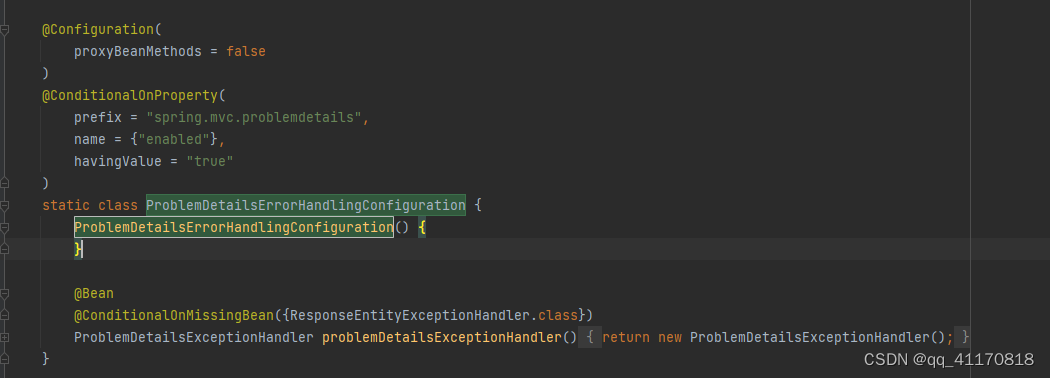在这里插入图片描述
ProblemDetailsExceptionHandler 容器中的一个组件

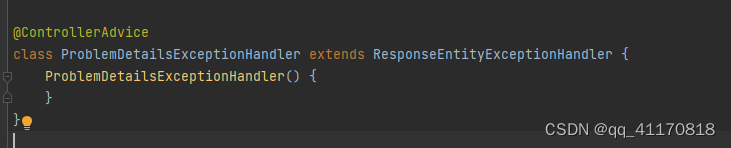
-@ControllerAdvice用来集中处理异常的

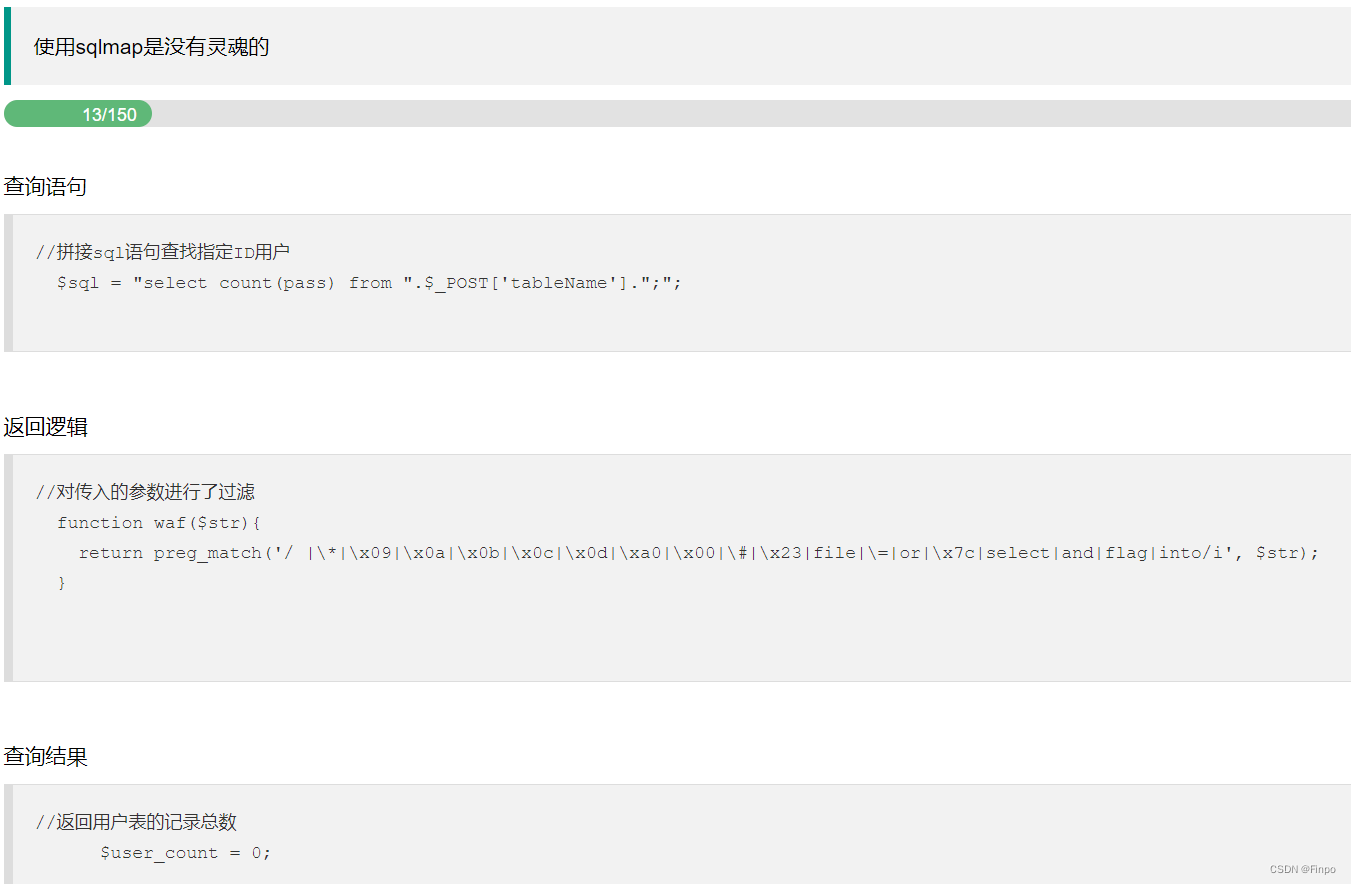
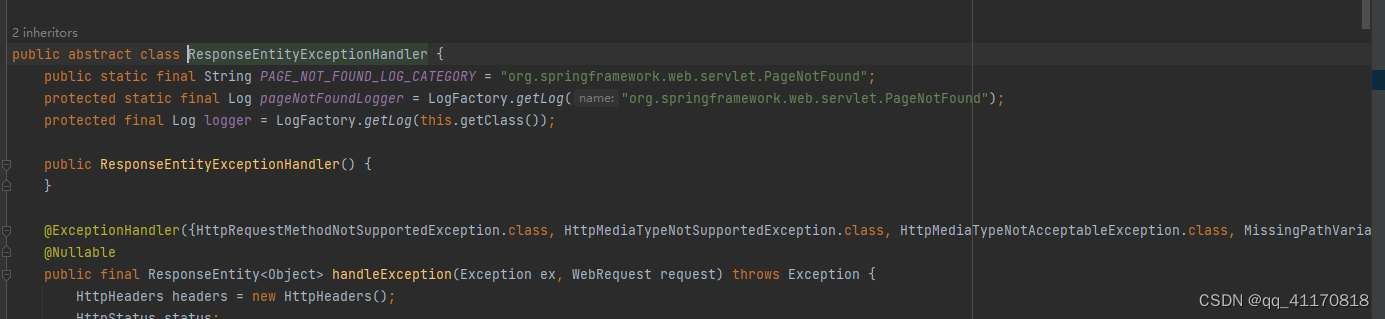
-点进ResponseEntityExceptionHandler 包含这些异常，如果出现以下异常，会被springboot支持以RFC 7807规范返回错误数据默认未开启
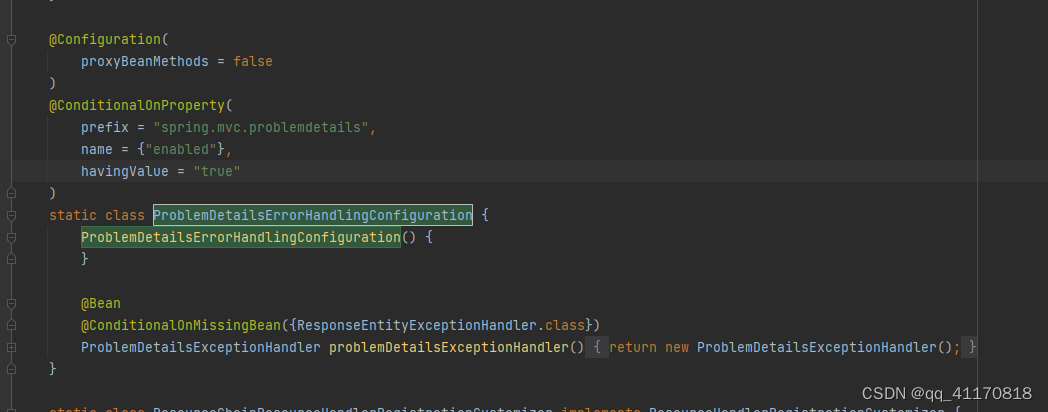
在这里插入图片描述

可以看到配置过这个spring.mvc.problemdetails
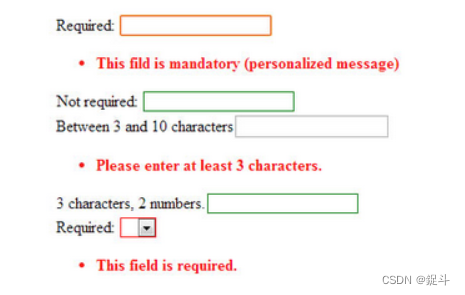
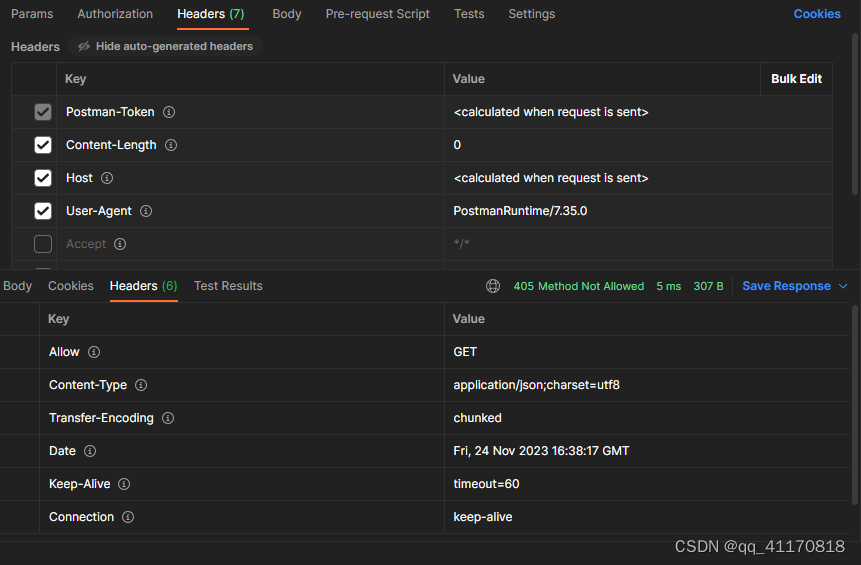
在这里插入图片描述
没开启的返回内容：

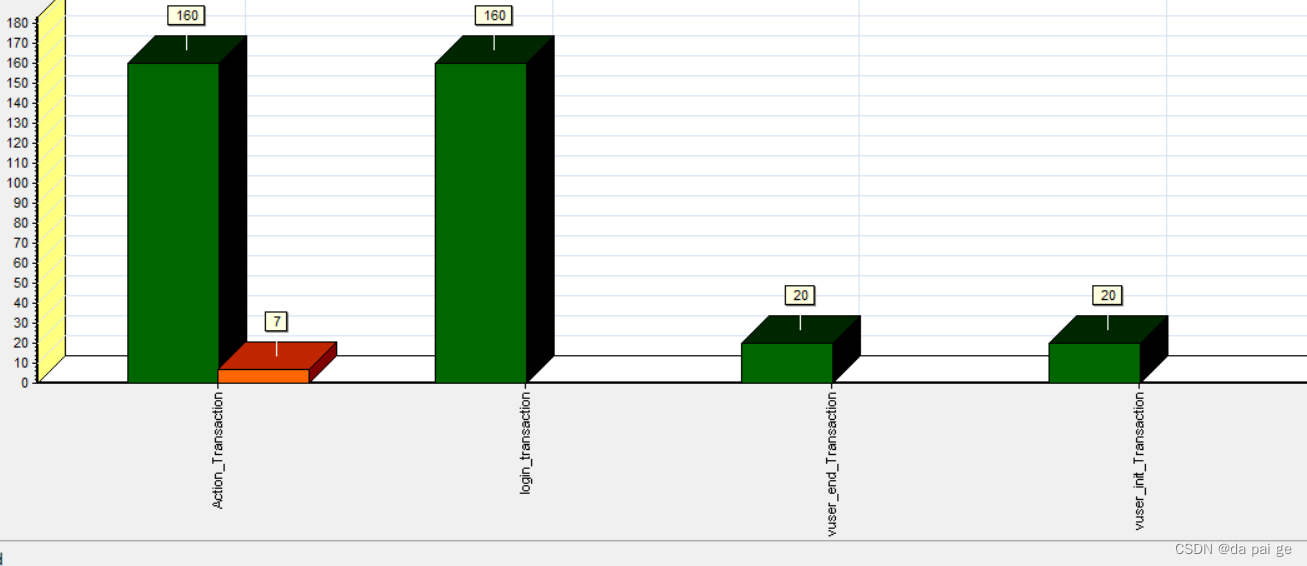
开启后：
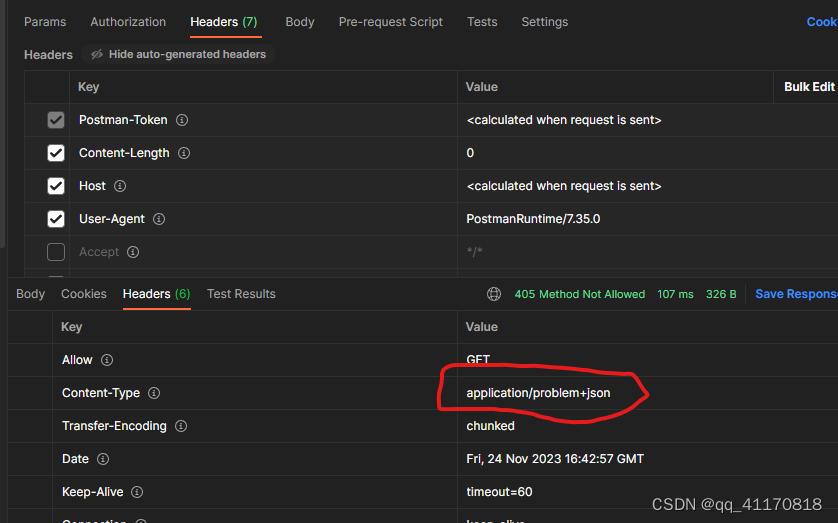
在这里插入图片描述
配置开启：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/216122.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

jQuery 第十一章（表单验证插件推荐）

文章目录前言jValidateZebra FormjQuery.validValValidityValidForm BuilderForm ValidatorProgressionformvalidationjQuery Validation PluginjQuery Validation EnginejQuery ValidateValidarium后言前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏&…

大众博客系统测试报告【改】

一、项目背景大众博客系统采用前后端分离的方法来实现，同时使用了数据库来存储相关的数据，同时将其部署到云服务器上。前端主要有四个页面构成：登录页、列表页、详情页以及编辑页，以上模拟实现了最简单的大众博客系统。其结合后端…

CPU+GPU多样化算力，ZStack Cloud助力游戏精酿核心业务上云

游戏精酿通过ZStack Cloud云平台提供高性能、高可用的云主机、云存储和云网络；前期通过超融合架构快速构建云基础设施，来支持Jira、Redis等关键业务；并实现对原有私有云平台业务的替代，按需将原有私有云业务滚动迁移到ZStack Clou…

nginx知识梳理及配置详解

软件开发全文档获取：点我获取 nginx安装 #nginx安装 yum -y install gcc pcre-devel openssl-devel #依赖包 useradd -s /sbin/nologin nginx ./configure --prefix/usr/local/nginx #指定安装目录 --usernginx #指定用户 --with-http_ss…

CTFSHOW sqll注入

号过滤绕过号和不加通配符的 like 是一样的。还可以使用 < >号来绕过，<> 在mysql中等于! 如果在加一个! 双重否定代表肯定就是了空格过滤绕过 /**/ ，()，，tab，两个空格 or and xor not 过滤绕过 a…

130. 面试官：vue生命周期是咋样的？父子组件直接触发的生命周期钩子顺序是咋样的...

130期 1. vue生命周期是咋样的？父子组件直接触发的生命周期钩子顺序是咋样的 2. 将图片进行base64编码后，为什么是会让图片变大？ 3. 说说webpack proxy工作原理，为什么能解决跨域问题？ 上面问题的答案会在第二天的公众…

Alibaba Cloud Linux 3安装Docker

进行docker安装（以社区版为例） 添加docker-ce的dnf源 dnf config-manager --add-repohttps://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo2.安装Alibaba Cloud Linux 3专用的dnf源兼容插件 dnf -y install dnf-plugin-releasever-adap…

qRT-PCR相对定量计算详解qPCR相对定量计算方式——2^-(∆∆Ct) deta t

做完转录组分析之后，一般都要求做qRT-PCR来验证二代测序得到的转录本表达是否可靠。荧光定量PCR是一种相对表达定量的方法，他的计算方法有很多，常用的相对定量数据分析方法有双标曲线法，ΔCt法，2^-ΔΔCt法(Livak法)&a…

Day40力扣打卡

打卡记录包子凑数（裴蜀定理 DP） 根据裴蜀定理，存在 c gcd(a, b) 使不定方程ax by c满足条件，如果gcd(a, b) 1即a与b互素的情况下，就会 ax by 1，由于为1可以构造后面的无穷数字，故得到结…

【2023 云栖】阿里云田奇铣：大模型驱动 DataWorks 数据开发治理平台智能化升级

云布道师本文根据 2023 云栖大会演讲实录整理而成，演讲信息如下： 演讲人：田奇铣 | 阿里云 DataWorks 产品负责人演讲主题：大模型驱动 DataWorks 数据开发治理平台智能化升级随着大模型掀起 AI 技术革新浪潮，大数…

性能测试【一】：Jmeter的常用操作

性能测试【一】：Jmeter的常用操作一、使用命令行方式运行Jmeter1、为什么2、怎么用3、示例4、结果文件二、生成动态报告1、准备2、命令3、报告示例4、报告释义三、使用问题汇总推荐使用命令行运行，GUI方式会经常卡死，尤其跑稳定性一、使…

01-概述 - OpenCV介绍与环境搭建

目录 1、OpenCV概念 （1）OpenCV 的介绍 （2）图像处理（Image Processing） （3）OpenCV的架构和核心模块 2、开发环境搭建 3、代码与演示 1、OpenCV概念 （1）…

springboot 返回problem+json

相关文章