进入贪心了，我觉得本专题是最烧脑的专题

Leetcode 455. 分发饼干

题目链接 455 分发饼干

让大的饼干去满足需求量大的孩子即是本题的思路：

class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int sum = 0;sort(g.begin(),g.end());sort(s.begin(),s.end());int result = 0;int index = s.size()-1;for(int i=g.size()-1;i>=0;i--){//胃口if(index>=0&&s[index]>=g[i]){//饼干量result++;index--;}}return result;}
};

ok,下面烧脑开始：

Leetcode 376. 摆动序列

题目链接 76 摆动序列

首先我们觉得本题目体现的贪心思想比较难想，我觉得这里应该用dp来写，但是竟然有贪心思想，就是贪心题目，那就烧脑一下吧：

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

整体思路：

出现摆动就记录一下。

对应代码就是：

如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。

除此之外我们还要考虑三点：

第一点：上下坡中有平坡：

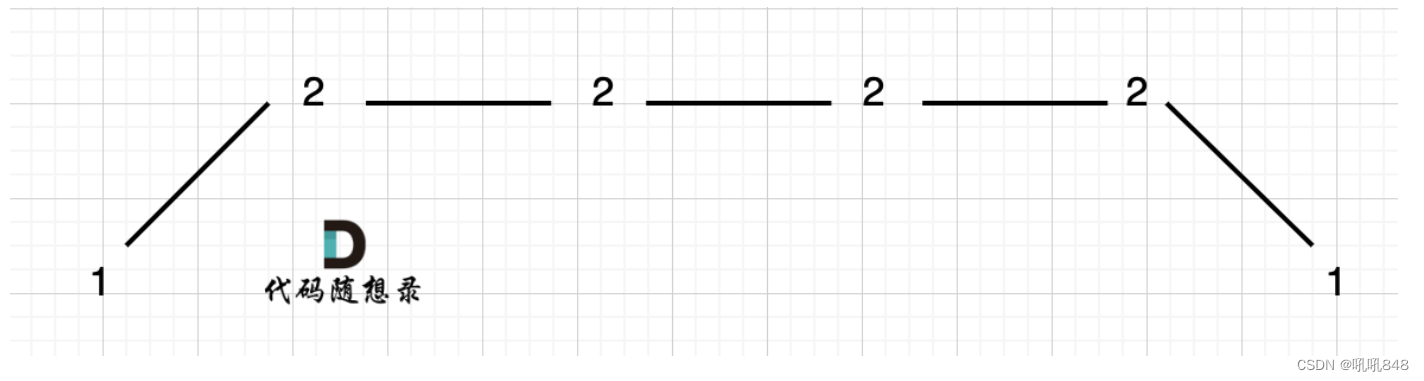
实际上我们取得摆动就三个，只需把中间四个2删除三个就行，这里我们只需记录即可，变成1——2——1即可，针对于代码来说就是：

(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，我们有波动就需要统计。

第二点：数组首尾两端

题目中说了，如果只有两个不同的元素，那摆动序列也是 2。

这里我们就需要建立一个虚拟节点（虚拟节点和数组开头组成preDiff == 0，即使平坡）使其满足preDiff和curDiff两边需要三个节点最基础的情况，这样我们就可将第二种情况算到第一种情况的代码中了：

(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，我们有波动就需要统计。

第三点：单调坡度有平坡（比较难想）

这时我们就不能实时更新preDiff了，我们只需在遇到(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)即摆动时我们preDiff。

下面上代码：

class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int result = 0;int preDiff = 0;int curDiff = 0;result++;for(int i=0;i<nums.size()-1;i++){curDiff = nums[i+1]-nums[i];if(preDiff>=0&&curDiff<0||preDiff<=0&&curDiff>0){result++;preDiff = curDiff;//摆动时更新}}return result;}
};

Leetcode 53. 最大子数组和

题目链接 53 最大子数组和

本题目很难发现需要使用贪心思想。

如果 -2 1 在一起，计算起点的时候，一定是从 1 开始计算，因为负数只会拉低总和，这就是贪心贪的地方！

局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。

全局最优：选取最大“连续和”

此外我们还需要不断记录连续和，找到最大的那个，就解决问题了。

下面上代码：

class Solution {
public:int maxSubArray(vector<int>& nums) {int count = 0;int result = INT_MIN;for(int i=0;i<nums.size();i++){count+=nums[i];if(count>result){result = count;}if(count<=0){//连续和为负数，直接抛弃count = 0;}}return result;}
};

end，学六级！！！