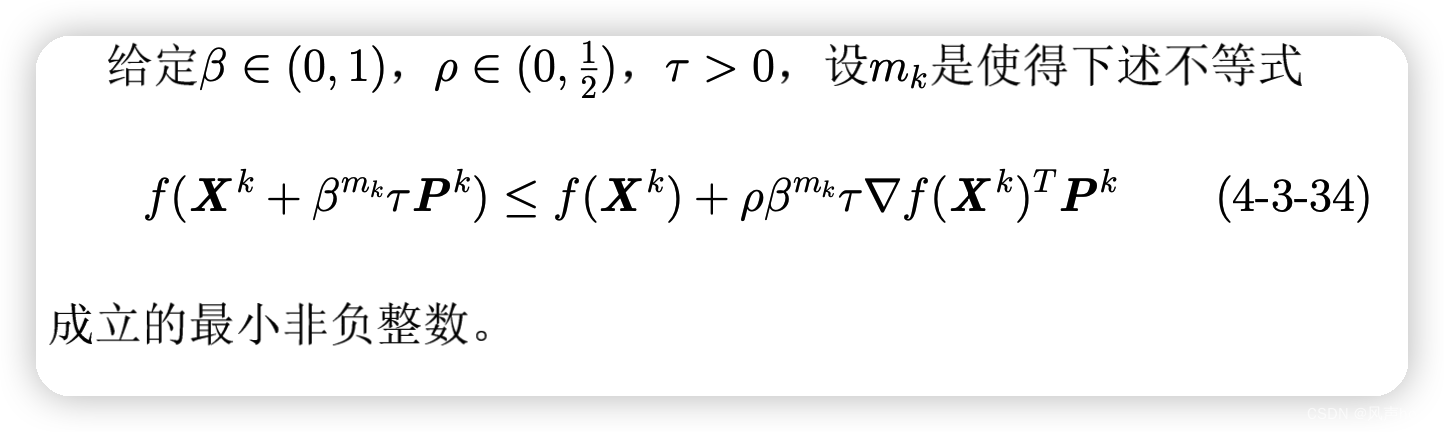最优化基础知识（2）

无约束优化问题，一维搜索

一、一维搜索

一维搜索的意思是在一个方向上找到最小点。

用数学语言描述，X^*=X^k +tP^k，从X^k沿着P^k方向行走t到达最小点X^*。

1、收敛速度：

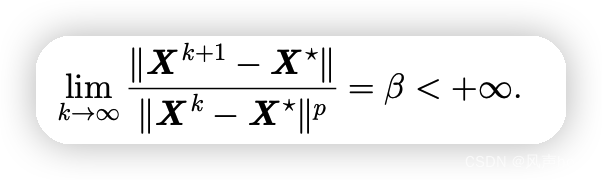
1. 线性收敛：p=1,0<beta<1
2. 超线性收敛: p>1或者beta=0
3. 次线性收敛：p=1，beta=1
4. p阶收敛：p>1

2、二次终止性：

能够在有限步内找到具有正定矩阵的二次函数的极小点。

f (X) = 1/2 X^TAX + b^TX + c

3、终止准则

什么时候停机，什么时候停止搜索。通常有以下五种：

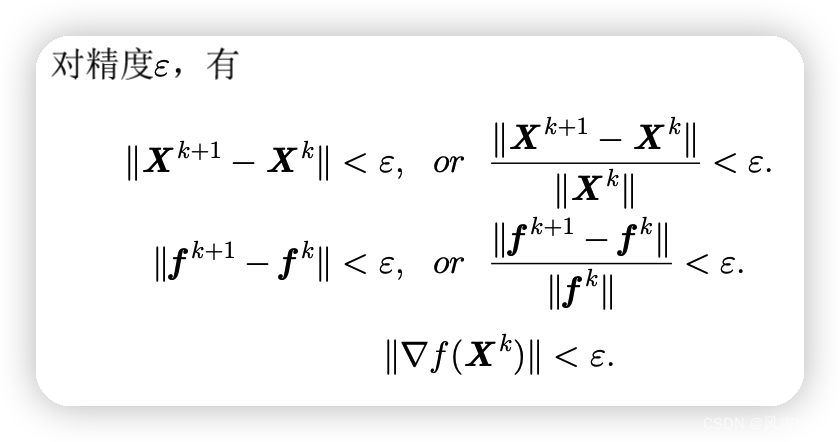
1、黄金分割法

给定每次迭代区间缩小比例，如果做才能搜索次数最少？

黄金分割法的python代码:

import mathdef golden_section_search(f, a, b, tol=1e-6):golden_ratio = (math.sqrt(5) - 1) / 2length = b - ax1 = a + (1 - golden_ratio) * lengthx2 = a + golden_ratio * lengthwhile x2-x1>tol:print(x1,x2)if f(x1) < f(x2):b = x2x2 = x1x1 = a + (1 - golden_ratio) * (b - a)else:a = x1x1 = x2x2 = a + golden_ratio * (b - a)return (a + b) / 2# 示例用法
def f(x):# 定义函数 f(x)return x*math.log(x)# 在区间 [0, 5] 中寻找函数的极小值点
result = golden_section_search(f, 0, 5)
print(f"极小值点的位置为: {result}")
print(f"函数极小值为: {f(result)}")

2、fibonacci搜索

给定迭代次数，如何在迭代次数内达到最好的搜索效果（最后一次迭代完成，搜索区间最小）？

这个问题可以反过来理解，假设最后一次迭代完成，搜索区间长度为1，那么最开始的搜索区间最大为多少？

python代码：

import mathdef fibonacci_search(f, a, b, n):# 计算Fibonacci数列fibonacci = [0, 1]for i in range(n):fibonacci.append(fibonacci[-1] + fibonacci[-2])# 计算初始区间长度length = b - a# 计算初始比例ratio = (fibonacci[-3] / fibonacci[-1]) if len(fibonacci) > 2 else 0# 初始化区间端点x1 = a + ratio * lengthx2 = a + (1 - ratio) * length# 迭代搜索for _ in range(len(fibonacci) - 3):if f(x1) < f(x2):b = x2x2 = x1x1 = a + ratio * (b - a)else:a = x1x1 = x2x2 = a + (1 - ratio) * (b - a)fibonacci.pop()ratio = (fibonacci[-3] / fibonacci[-1])print(fibonacci[-3],fibonacci[-1],ration)# 返回最优解的位置return (a + b) / 2# 示例用法
def f(x):# 定义函数 f(x)return x*math.log(x)# 在区间 [-5, 5] 中寻找函数的极小值点
result = fibonacci_search(f, 0, 5, 30)
print(f"极小值点的位置为: {result}")
print(f"函数极小值为: {f(result)}")

在有的地方，直接给出的不是迭代次数，而是最终的区间长度的上界L，b1-a1是初始区间。
$$b_n-a_n=F_{n-1}/F_n(b_{n-1}-a_{n-1})=\frac{F_{n-1}}{F_n}\frac{F_{n-2}}{F_{n-1}}\cdots \frac{F_1}{F_2}(b_1-a_1)$$
也就是说区间长度最小bn-an=（b1-a1）/F_n<=L，F_n是最大的fibonacci数。

关键：F[n-2]+F[n-1]=F[n]，F[n-2]/F[n]+F[n-1]/F[n]=1，这样能保证每次删掉一侧的区间，比例是一样的。

当F[6]/F[7]=21/34=0.6176470588235294，和黄金分割法近似相同。

黄金分割法是fibonacci法的极限形式。

3、三点二次插值法

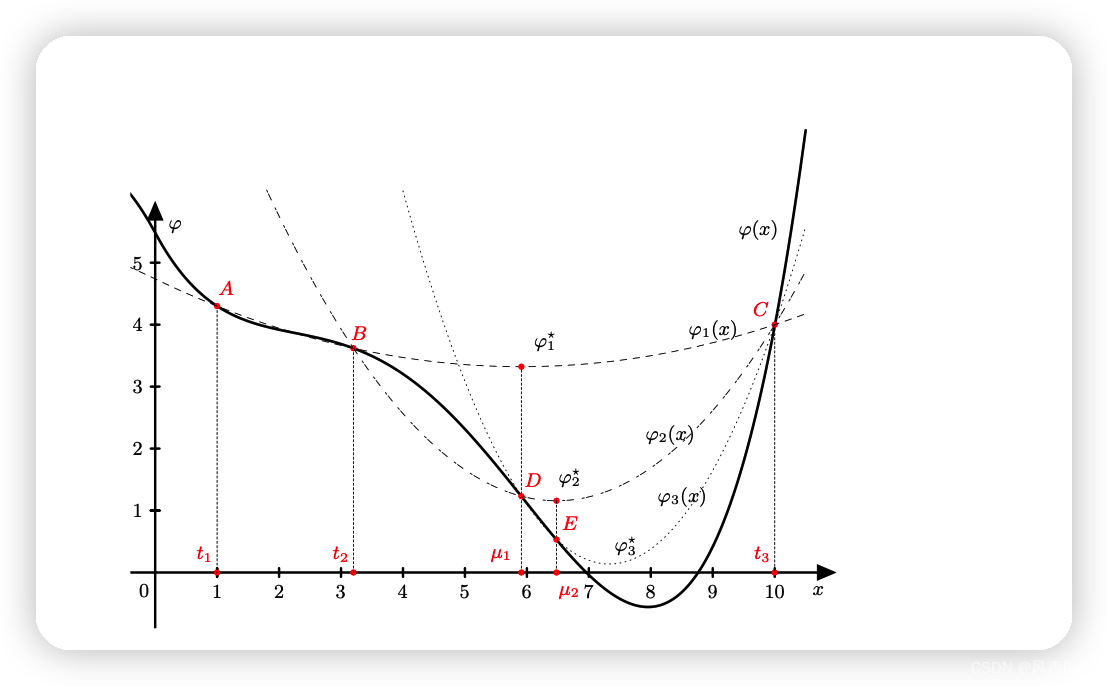
4、两点三次插值法

5、牛顿法

牛顿法就是在极小点附近选择一个初始点x0，在x0处二阶泰勒展开，并求其驻点。牛顿法不具有全局收敛性，因此初始点的选择很重要，它只是向初始点附近的驻点靠近。

牛顿法的python代码：

import sympy as sp
def newton_method(f, x0, tol=1e-6, max_iter=100):f_d1 = f.diff()f_d2 = f_d1.diff()# 迭代搜索for _ in range(max_iter):# 计算导数值fx = f_d1.subs({x:x0})fxx = f_d2.subs({x:x0})# 更新搜索位置x1 = x0 - fx / fxx# 检查是否满足终止条件if abs(x1 - x0) < tol:break# 更新当前点x0 = x1# 返回搜索结果return x1# 示例用法
x = sp.Symbol('x')
f=x**3-4*x+5# 选择初始点
x0 = -10# 使用牛顿法搜索函数的极小值点
result = newton_method(f, x0)
print(f"极小值点的位置为: {result.n()}")
print(f"函数极小值为: {f.subs({x:result}).n()}")

二、非精确一维搜索

1、Goldstein准则

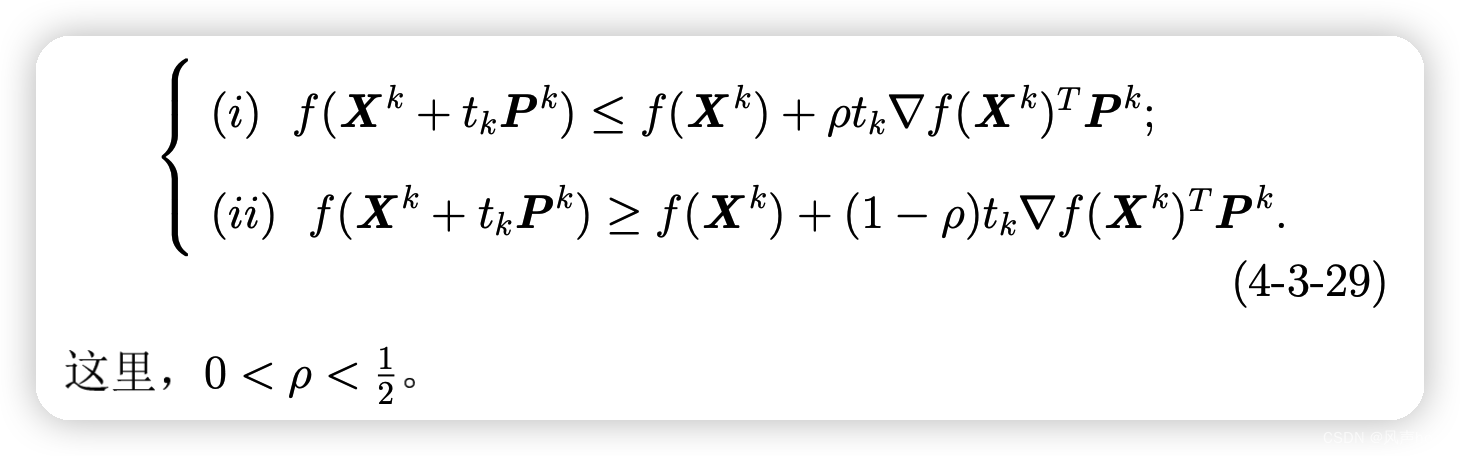
2、Wolfe准则

3、Armijo准则