Leetcode—55.跳跃游戏【中等】-编程知识

Leetcode—55.跳跃游戏【中等】

2023每日刷题（四十）

Leetcode—55.跳跃游戏

在这里插入图片描述

贪心法实现代码

#define MAX(a, b) ((a > b)? (a): (b))bool canJump(int* nums, int numsSize) {int k = 0;for(int i = 0; i < numsSize; i++) {if(i > k) {return false;}k = MAX(k, i + nums[i]);}return true;
}

运行结果

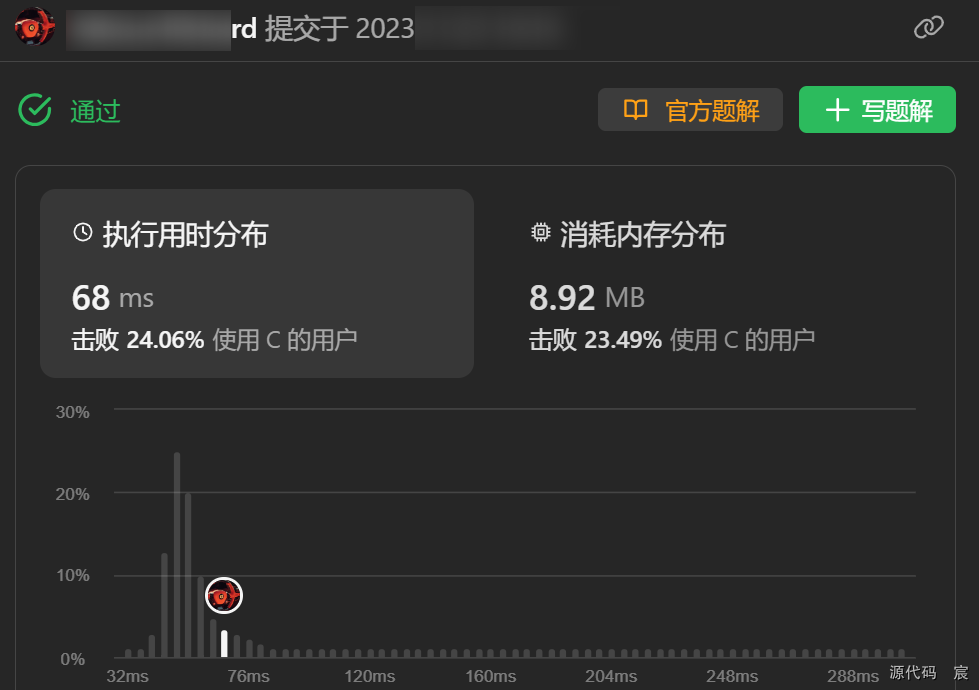
在这里插入图片描述
复杂度分析
●　时间复杂度：O(n)，其中n为数组长度。
●　空间复杂度：O(1)。

动态规划思想

模拟整个过程，可以发现数组中的每个位置能否到达都依赖于前面的位置。只要前面某个位置可达，并且它的最大跳跃长度能够达到目标位置，那么目标位置也是可达的。

每个位置都有可达和不可达两种状态，并且跳跃的过程可以模拟为状态转移的过程，因此这个问题可以尝试使用动态规划去解决。

设计布尔值dp[i]表示状态，True为可达，False为不可达，从左到右依次遍历每个位置，每次通过前面的位置来求解当前位置是否可达。状态转移方程为dp[i]=dp[i]or dp[j](0 <=j < i 且j+nums[j]>=i)，其中i为当前求解位置的下标，j为前面位置的下标，nums[j]为前面位置可以跳跃的最大长度。

bool canJump(int* nums, int numsSize) {bool dp[numsSize];memset(dp, false, numsSize);dp[0] = true;for(int i = 1; i < numsSize; i++) {for(int j = 0; j < i; j++) {if(j + nums[j] >= i) {dp[i] = dp[i] || dp[j];}}}return dp[numsSize - 1];
}

复杂度分析
●　时间复杂度： $O(n^2)$ ，其中n为数组长度。
●　空间复杂度：O(n)，其中n为数组长度。
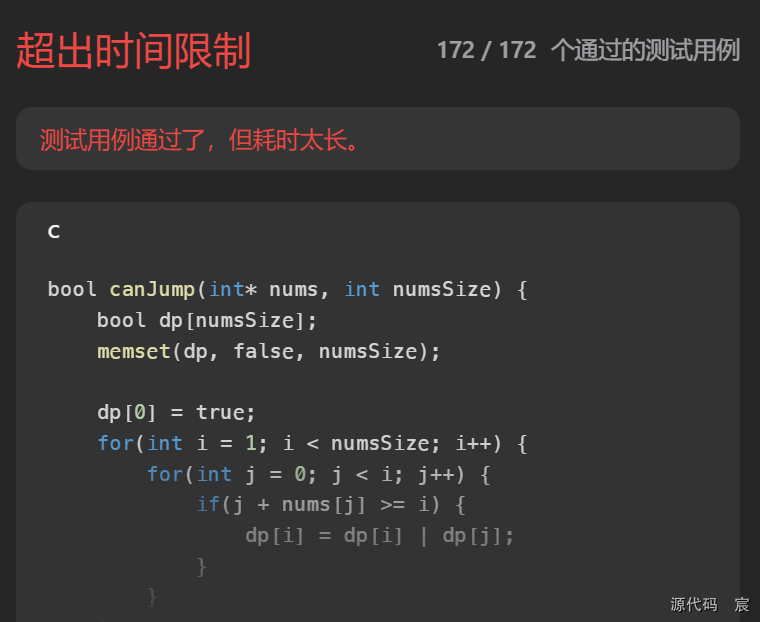
在这里插入图片描述
重新观察一下整个循环的过程，每次为了判断第i个位置是否可达（外循环），我们都需要考虑从0到i-1上的位置信息（内循环），显然前面位置上的信息都会不断重复地被考虑。

优化的方法就是改变dp[i]状态的含义，让dp[i]能够表示所有前面的位置信息，而不仅仅表示自身位置是否可达。上面的内循环实际上在考虑前面位置所能到达的最远位置是否大于当前位置，因此可以让dp[i]表示起点为0到i的位置所能到达的最远位置。考虑前i-1个位置能否到达i，具体如下。

●　如果不能到达i，则不能从i起跳，前i个位置所能到达的最远位置就是dp[i-1]。
●　如果能到达i，则可以从i起跳，前i个位置所能到达的最远位置就是起点为i能够起跳的最远位置和前i-1个位置所能到达的最远位置这两者的较大值。
在这里插入图片描述

#define MAX(a, b) (a > b ? (a): (b))
bool canJump(int* nums, int numsSize) {int dp[numsSize];memset(dp, 0, numsSize);dp[0] = nums[0];for(int i = 1; i < numsSize; i++) {if(dp[i - 1] < i) {dp[i] = dp[i - 1];} else {dp[i] = MAX(dp[i - 1], i + nums[i]);}}if(dp[numsSize - 1] < numsSize - 1) {return false;}return true;
}

实现代码

#define MAX(a, b) (a > b ? (a): (b))
bool canJump(int* nums, int numsSize) {int pre = nums[0];int cur = pre;for(int i = 1; i < numsSize; i++) {if(pre < i) {cur = pre;} else {cur = MAX(pre, i + nums[i]);}pre = cur;}if(pre < numsSize - 1) {return false;}return true;
}