【刷题宝典NO.5】-编程知识

有效的括号

https://leetcode.cn/problems/valid-parentheses/

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：
输入：s = "()"
输出：true
示例 2：
输入：s = "()[]{}"
输出：true
示例 3：
输入：s = "(]"
输出：false
提示：

1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成

class Solution {public boolean isValid(String s) {/*([)]())(())()*/Stack<Character> stack = new Stack<>();for (int i = 0; i < s.length(); i++) {char ch = s.charAt(i);//ch: ( ) { } [ ]//遍历字符串取出每个字符之后进行操作//如果是左括号if (ch == '(' || ch == '[' || ch == '{') {//就入栈stack.push(ch);//stack里面一定是左括号} else {//如果是右括号 if (stack.empty()) {//且栈空，说明右括号多，不匹配return false;} char ch2 = stack.peek();//查看栈顶元素, 判断是否跟遍历的右括号匹配, 匹配就出栈if (ch == ')' && ch2 == '(' || ch == ']' && ch2 == '[' || ch == '}' && ch2 == '{') {stack.pop();} else {//不匹配return false;}}}//遍历完了，且栈不为空，说明此时左括号多，不匹配if (!stack.empty()) {return false;}//遍历完了，且栈为空，匹配return true;//或者直接判断栈空，因为此时字符串肯定遍历完了的// return stack.empty();}
}

括号的最大嵌套深度

https://leetcode.cn/problems/maximum-nesting-depth-of-the-parentheses/

如果字符串满足以下条件之一，则可以称之为 有效括号字符串（valid parentheses string，可以简写为 VPS）：

字符串是一个空字符串 ""，或者是一个不为 "(" 或 ")" 的单字符。
字符串可以写为 AB（A 与 B 字符串连接），其中 A 和 B 都是 有效括号字符串 。
字符串可以写为 (A)，其中 A 是一个 有效括号字符串 。

类似地，可以定义任何有效括号字符串 S 的 嵌套深度 depth(S)：

depth("") = 0
depth(C) = 0，其中 C 是单个字符的字符串，且该字符不是 "(" 或者 ")"
depth(A + B) = max(depth(A), depth(B))，其中 A 和 B 都是 有效括号字符串
depth("(" + A + ")") = 1 + depth(A)，其中 A 是一个 有效括号字符串

例如：""、"()()"、"()(()())" 都是 有效括号字符串（嵌套深度分别为 0、1、2），而 ")(" 、"(()" 都不是 有效括号字符串 。

给你一个 有效括号字符串 s，返回该字符串的 s 嵌套深度 。

示例 1：
输入：s = "(1+(2*3)+((8)/4))+1"
输出：3
解释：数字 8 在嵌套的 3 层括号中。
示例 2：
输入：s = "(1)+((2))+(((3)))"
输出：3
提示：

1 <= s.length <= 100
s 由数字 0-9 和字符 '+'、'-'、'*'、'/'、'('、')' 组成
题目数据保证括号表达式 s 是 有效的括号表达式

逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：
输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9
示例 2：
输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6
示例 3：
输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示：

1 <= tokens.length <= 104
tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

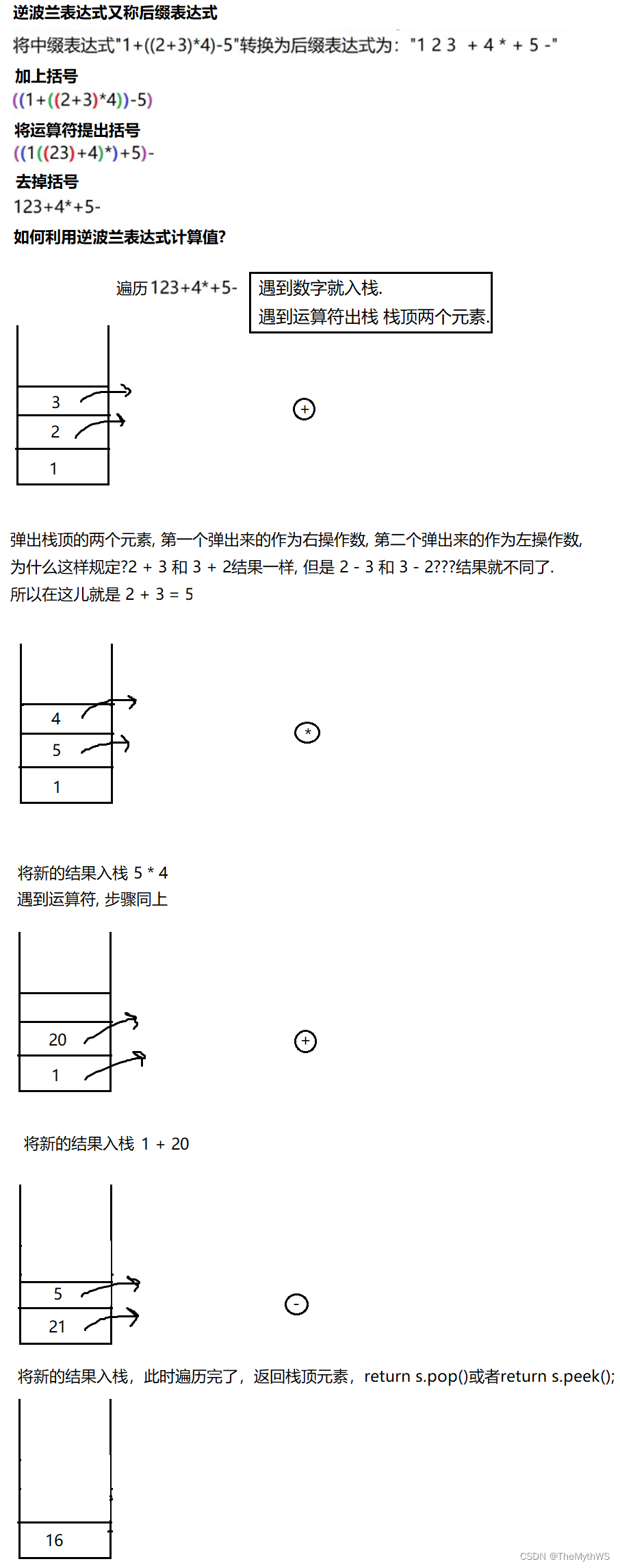
逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for (String x : tokens) {if (!isOperation(x)) {//是数字就入栈stack.push(Integer.parseInt(x));} else {//是操作符就取出两个元素int num2 = stack.pop();//第二个操作数, 栈顶先弹出int num1 = stack.pop();//第一个操作数switch (x) {case "+":stack.push(num1 + num2);break;case "-":stack.push(num1 - num2);break;case "*":stack.push(num1 * num2);break;case "/":stack.push(num1 / num2);break;}}}return stack.pop();//peek()}private boolean isOperation(String x) {return (x.equals("+") || x.equals("-") || x.equals("/") || x.equals("*"));}
}