仅作自己学习使用
一、问题
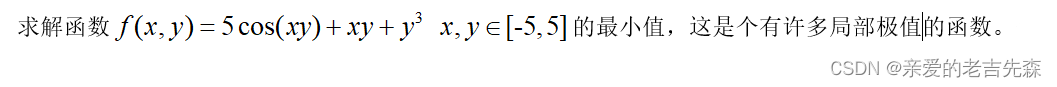
二、代码
clear
clcT1 = cputime;
xmax = 5;
xmin = -5;
ymax = 5;
ymin = -5;
L = 20; % 马尔科夫链长度
dt = 0.998; % 降温系数
S = 0.02; % 步长因子
T = 200; % 初始温度
TZ = 1e-8; % 容差
Tmin = 0.01;% 最低温度
P = 0; % Metropolis接受准则中接受的点的个数
PreX = rand*(xmax - xmin) + xmin; % (设置初始x的位置)上一个搜索的x值
PreY = rand*(ymax - ymin) + ymin; % (设置初始y的位置)上一个搜索的y值
PreBestX = PreX; % 上一个最优秀的x值
PreBestY = PreY; % 上一个最优秀的y值
PreX = rand*(xmax - xmin) + xmin; % 上一个搜索的x值
PreY = rand*(ymax - ymin) + ymin; % 上一个搜索的y值
BestX = PreX; % 最优秀的X值
BestY = PreY; % 最优秀的y值
trace = []; % 用于记录历代最优解的函数值
deta = abs(eval(BestX,BestY) - eval(PreBestX,PreBestY)); % 上一次最小值和这次最小值的差的绝对值
while (deta>TZ) && (T>0.01)% 在当前温度下迭代L次数for i = 1: L% 在当前点附件随机的选取下一点P = 0;while P==0NextX = PreX + S*(rand*(xmax-xmin) + xmin);NextY = PreY + S*(rand*(ymax-ymin) + ymin);if (NextX >= xmin && NextX <= xmax && NextY >= ymin && NextY <= ymax)P = 1;endend% 判断选取的这个(x,y)对应的函数值是否比上一个选出来的最优值更优秀if(eval(NextX,NextY)<eval(BestX,BestY))% 保留上一个最优解PreBestX = BestX;PreBestY = BestY;% 更新最优解BestX = NextX;BestY = NextY;end% Metropolis接受准测 接受过程if(eval(NextX,NextY) < eval(PreX,PreY))% 当前解更优秀,接受新解PreX = NextX;PreY = NextY;P = P +1;else% 当前解更差,概率接受更差的解P1 = exp((eval(PreX,PreY)-eval(NextX,NextY))/T); % 接受的概率if P1 > randPreX = NextX;PreY = NextY;P = P + 1;endendtrace = [trace eval(BestX,BestY)];enddeta = abs(eval(BestX,BestY) - eval(PreBestX,PreBestY));% 本次退火过程结束,温度下降T = T * dt;
end
T2 = cputime;
timeConsume = T2 - T1;
%% 绘图适配值最优化曲线
figure(1)
disp("最小值点在:")
BestX
BestY
disp("最小值为:")
eval(BestX,BestY)
plot(trace,LineWidth=1,Color=[0.68 0.52 0.96])
xlabel("迭代次数")
ylabel("目标函数值")
title("适配值最优化曲线","时间消耗:" + timeConsume )
%% 做出函数图像
figure(2)
x = -5:0.01:5;
y = -5:0.01:5;
N = length(x);
for i = 1 : Nfor j = 1 : Nz(i,j) = 5*cos(x(i)*y(j)) + x(i)*y(j) + y(j)^3;end
end
colormap('jet')
mesh(x,y,z)
grid on
xlabel('x')
ylabel('y')
zlabel('f(x,y)')
hold on
plot3(BestX,BestY,eval(BestX,BestY),'r*')
text(BestX,BestY,eval(BestX,BestY), '最小值点', 'FontSize', 15, 'HorizontalAlignment', 'left');%% 评估函数(目标函数)
function result = eval(x,y)result = 5 * cos(x*y) + x*y + y^3;
end
三、效果
3.1 适配值最优化曲线
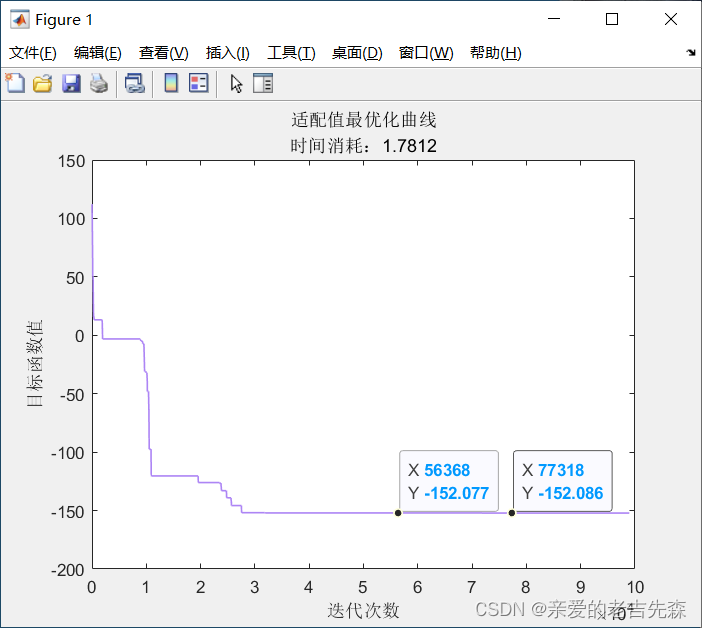
3.2 多次求解结果在函数图像中的表现
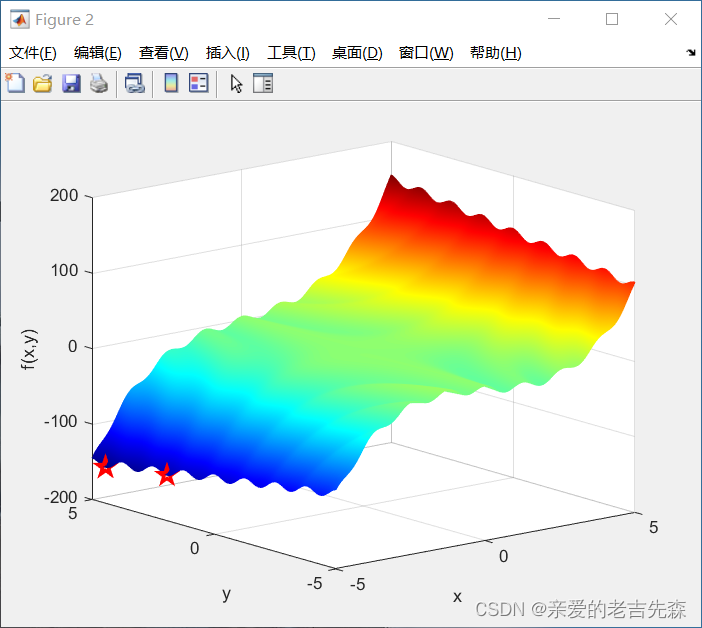
图中五角星就是求解出来的极值点,发现仍然会有部分会落在局部极值点的情况,陷入了局部最优。
四、问题
跑过的朋友可以发现,如果按照上述代码,画出来的极值点应该是这样的:
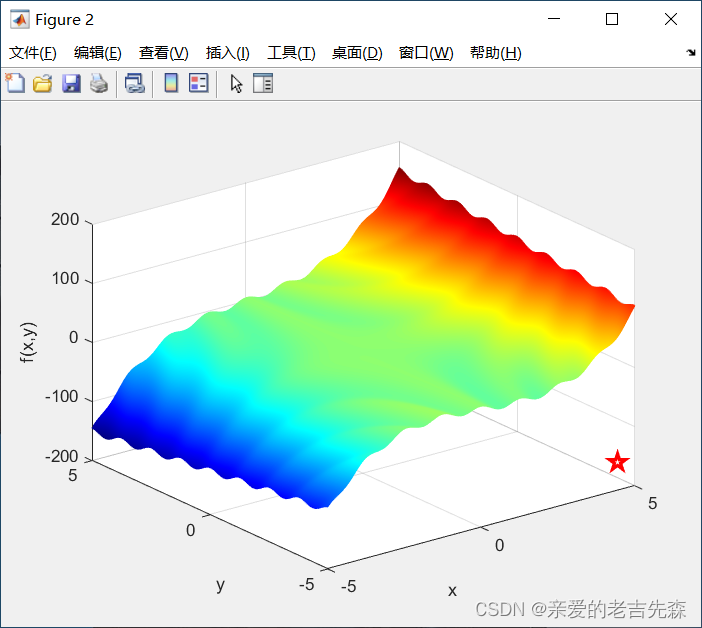
那么我做了什么调整呢:我把绘图点的x,y坐标交换了一下:
plot3(BestX,BestY,eval(BestX,BestY),'rp',MarkerSize=10,LineWidth=2)
为什么会交换呢?因为我发现x,y的值求反了,BestX里边存的是Y的坐标,BestY里边存放的是X坐标;
还有一个问题是,关于x,y的随机跳动:
NextX = PreX + S*(rand*(xmax-xmin) + xmin);
NextY = PreY + S*(rand*(ymax-ymin) + ymin);
它是与温度无关的,在我求解一维函数的极值问题中我也提到了。
请知道bug的朋友在评论区留言,我将及时改正!