1.产生一个幅度为1, 基频为2Hz,占空比为50%的周期方波.要求画出图形。
在MATLAB中,函数square(w0*t, DUTY)产生基本频率为w0 (周期T=2*pi/w0)、占空比DUTY= (τ/T)*100的周期矩形波(方波),默认情况下占空比DUTY=50。占空比指的是一个周期内,矩形波正电压持续的时间占整个周期的比例,即τ为一个周期中信号为正的时间长度,如果τ=T/2,那么DUTY=50,square(w0*t, 50)等同于square(w0*t)。
程序:
t=-4:0.0001:4;
A=2;T=pi;w0=2*pi/T;
ft=(1/2)*A*square(w0*t,50)+(1/2);
plot(t,ft);
axis([-4,4,-2,2]);运行结果:

2.产生一个Sa函数,理论上抽样信号Sa函数的定义为:
(要求画出图形)
MATLAB中有专门的命令sinc()产生抽样信号Sa函数.
程序:
t=-2*pi:0.01:2*pi;
y=sinc(t);
plot(t,y)
grid on运行结果:

3.已知系统的微分方程为:
求该系统的单位冲击响应并画图。注意:impulse调用格式
程序:
sys = tf([1, 3],[1, 3, 2]);
t = 0:0.1:10;
y = impulse(sys, t);
plot(t, y);运行结果:

4. 已知x1(n)= [1,1,1,0,1]-3,x2(n) = [2,2,2,2]-1
求:x(n) = x1(n) + x2(n) ,x(n) = x1(n) x2(n),并画图。
程序:
x1=[1,1,1,0,1];
ns1=-3;
x2=[2,2,2,2];
ns2=-1;
nf1=ns1+length(x1)-1;
nf2=ns2+length(x2)-1;
ny=min(ns1,ns2):max(nf1,nf2);
xa1=zeros(1,length(ny));xa2=xa1;
xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;
xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;
ya=xa1+xa2
yp=xa1.*xa2
subplot(4,1,1),stem(ny,xa1,'.')
subplot(4,1,2),stem(ny,xa2,'.')
line([ny(1),ny(end)],[0,0])
subplot(4,1,3),stem(ny,ya,'.')
line([ny(1),ny(end)],[0,0])
subplot(4,1,4),stem(ny,yp,'.')
line([ny(1),ny(end)],[0,0])运行结果:
ya =
1 1 3 2 3 2
yp =
0 0 2 0 2 0


5.利用函数impz和stepz求离散系统

的单位序列响应h(k)和单位阶跃响应g(k)。
程序:
a=[1 0 1/3 0];
b=[1/6 1/2 1/2 1/6];
N=32;
n=0:N-1;hn=impz(b,a,n);
gn=dstep(b,a,n+1);
subplot(1,2,1),stem(n,hn);
title('系统单位冲激函数')
axis([0 N 1.1*min(hn) 1.1*max(hn)])subplot(1,2,2),stem(n,gn);
title('系统单位阶跃函数')
axis([0 N 1.1*min(gn) 1.1*max(gn)])运行结果:

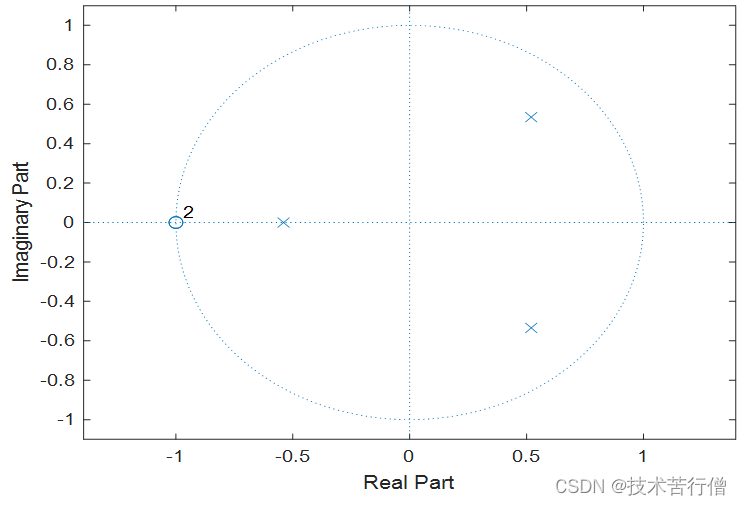
6.已知一离散因果系统的系统函数为:
利用MATLAB求出系统函数的零点和极点,并在Z平面显示它们的分布。
在MATLAB中可以借助函数tf2zp来直接得到系统函数的零点和极点的值,并通过函数zplane来显示其零点和极点的分布。
程序:
b=[1 2 1];
a=[1 -0.5 -0.005 0.3];
[z,p,k]=tf2zp(b,a);
B=[0 1 2 1];
A=[1 -0.5 -0.005 0.3];
figure
zplane(B,A);运行结果: