线性表定义:
由n (n≥0)个数据特性相同的元素构成的有限序列称为线性表,(n=0)的时候被称为空表。
线性表的顺序表示
线性表的顺序存储又被称为顺序表
-
优点
- 无需为表示表中元素之间的逻辑关系而增加额外的存储空间
- 可以随意读取任意位置的元素
-
缺点
-
插入或者删除,需要移动大量数据元素
-
线性表长度变化较大时,难以确定存储空间的容量
-
造成存储空间的碎片
-
java中用数组表示的:
double[] a = new double[N];
声明初始化数组:
int[] a = { 1, 1, 2, 3, 5, 8 };
数组一经创建,它的大小就是固定的。程序能够通过 a.length 获取数组 a[] 的长度,而它的最后一个元素总是 a[a.length – 1]。
典型的数组处理代码:
找出数组中最大的元素
double max = a[0];
for (int i = 1; i < a.length; i++)if (a[i] > max) max = a[i];
计算数组元素的平均值
int N = a.length;
double sum = 0.0;
for (int i = 0; i < N; i++)sum += a[i];
double average = sum / N;
复制数组
int N = a.length;
double[] b = new double[N];
for (int i = 0; i < N; i++)b[i] = a[i];
颠倒数组元素的顺序
int N = a.length;
for (int i = 0; i < N/2; i++)
{double temp = a[i];a[i] = a[N-1-i];a[N-i-1] = temp;
}
矩阵相乘(方阵) a[] [ ] * b[] [] = c[] []
int N = a.length;
double[][] c = new double[N][N];
for (int i = 0; i < N; i++)for (int j = 0; j < N; j++){ // 计算行 i 和列 j 的点乘for (int k = 0; k < N; k++)c[i][j] += a[i][k]*b[k][j];}
二维数组
在 Java 中二维数组就是一维数组的数组。大多数情况下(根据合适的参数 M 和 N)我们都会使用 M×N,即 M 行长度为 N 的数 组的二维数组(也可以称数组含有 N 列)。
二维数组 a[][] 的 第 i 行第 j 列的元素可以写作 a [i] [j]
创建时:double[] [] a = new double [M] [N]
其根本是等价于:
double[][] a;
a = new double[M][N];
for (int i = 0; i < M; i++)for (int j = 0; j < N; j++)a[i][j] = 0.0;Java 会将数值类型的数组元素初始化为 0,将布尔型的数组元素初始化为 false。但是如果想要初始化为其他值,我们就需要嵌套的 for 循环设置自己想要的值。
稀疏数组 (sparsearray)
比如像五子棋棋盘,用二维数组存棋盘上的点。假设0为空,1是黑棋,2是白棋;那么前面会有很多默认值0,这样子记录了很多没价值的数据。这个时候就是稀疏数组的用武之地。
一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组来保存该数组。
稀疏数组的处理方法是:
-
记录数组一共有几行几列,有多少个不同的值
-
把具有不同值的元素的行列及值记录在一个小规模的数组中,从而缩小程序的规模
具体实施:
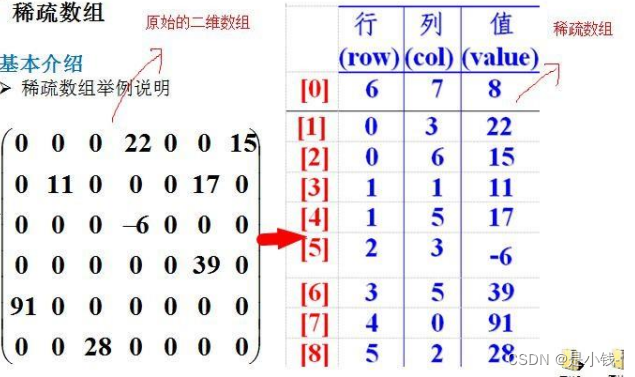
固定是3列。第一行是共有几行几列,有多少个不同的值 ,后面则是将每个特殊的元素所在的行列和值记录下来。
二维数组 转 稀疏数组的思路
1.遍历原始的二维数组,得到有效数据的个数sum
// 前面已经创建了原始二维数组,且用0表示没有棋子,1表示黑棋 2表示白棋int sum = 0;
for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr1[i][j] != 0) {sum++;}}
}
2.根据sum就可以创建稀疏数组sparseArr int [sum+1] [3]
int sparseArr[][] = new int[sum + 1][3];3.将二维数组的有效数据数据存入到稀疏数组
// 给稀疏数组赋值
sparseArr[0][0] = 11;
sparseArr[0][1] = 11;
sparseArr[0][2] = sum;
// 遍历二维数组,将非 0 的值存放到 sparseArr 中
int count = 0; //count 用于记录是第几个非 0 数据
for (int i = 0; i < 11; i++) {for (int j = 0; j < 11; j++) {if (chessArr1[i][j] != 0) {count++;sparseArr[count][0] = i; //row列记录行sparseArr[count][1] = j; //col列记录列sparseArr[count][2] = chessArr1[i][j]; //value列记录值}}
}
稀疏数组转原始的二维数组的思路
1.先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的 chesArr2=int[11] [11]
int chessArr2[][] = new int[sparseArr[0][0]][sparseArr[0][1]];
2.再读取稀疏数组后几行的数据,并赋给 原始的二维数组 即可
for(int i = 1; i < sparseArr.length; i++) {// 二维数组【行=稀疏数组[i][0]行的值】【列=稀疏数组[i][1]列的值】//= 值(稀疏数组第三列的值)chessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}