977. 有序数组的平方

难度：easy

类型：双指针（相向指针）

思路：

暴力法是将每个数都平方后，再排序(快排)，时间复杂度为O(logn)。我们采用双指针（相向指针，区别下一题的快慢指针）的方法，因为最大的平方数一定出现在数组首或尾，所以我们依次比较首位平方元素，从大到小来构建答案数组。

代码：

class Solution {public int[] sortedSquares(int[] nums) {int len = nums.length;int[] result = new int[len];int left = 0;int right = len - 1;for (int i = len - 1; i >= 0; i--) {if (nums[left] * nums[left] > nums[right] * nums[right]) {result[i] = nums[left] * nums[left];left++;} else {result[i] = nums[right] * nums[right];right--;}}return result;}
}

复杂度分析：

时间复杂度：O(n)

209. 长度最小的子数组

难度：easy

类型：双指针（快慢指针）

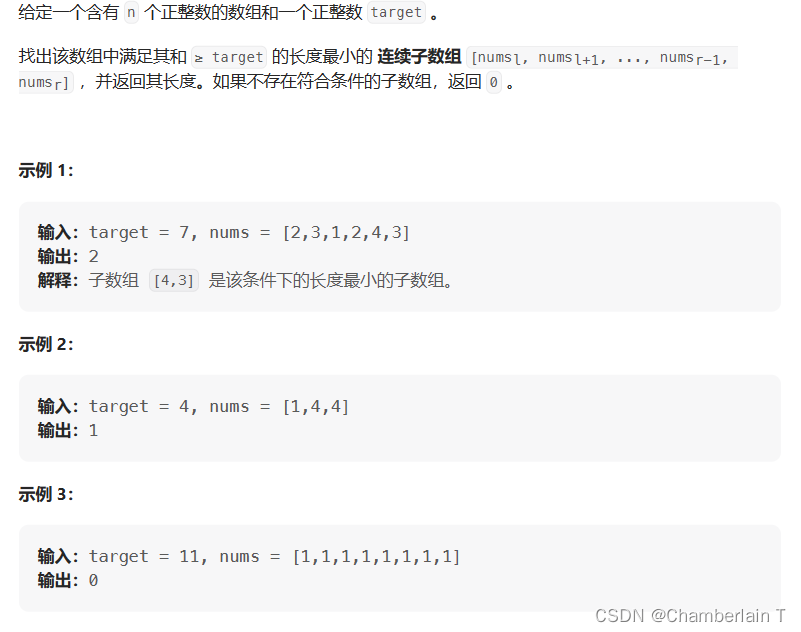思路：

这道题也可以通过暴力法解决，用两个for循环遍历所有情况，时间复杂度为O(n^2)。我们通过双指针来实现滑动窗口来解决这道题。窗口内的和为sum，right指针向右移动，当sum大于等于target时，判断是否为最小长度；然后左指针向左移直到sum小于target。

细节：

ans取Integer.MAX_VALUE，有助于动态更新最小长度；

ans = Integer.MAX_VALUE

代码：

class Solution {public int minSubArrayLen(int target, int[] nums) {int len = nums.length;int left = 0;int right = 0;int sum = 0;int ans = Integer.MAX_VALUE;while (right < len) {sum += nums[right++];while (sum >= target) {ans = Math.min(ans, right - left);sum -= nums[left++];}}return ans == Integer.MAX_VALUE? 0: ans;}
}

复杂度分析：

时间复杂度：
空间复杂度：

59. 螺旋矩阵 II

思路：

设置四个边界，动态更新边界，这样可以避免设置左闭右开区间，没那么麻烦。

代码：

class Solution {public int[][] generateMatrix(int n) {int[][] ans = new int[n][n];int left = 0;int right = n - 1;int up = 0;int down = n - 1;for (int element = 1; element <= n * n;) {for (int i = left; i <= right; i++) {ans[up][i] = element++;}up++;for (int i = up; i <= down; i++) {ans[i][right] = element++;}right--;for (int i = right; i >= left; i--) {ans[down][i] = element++;}down--;for (int i = down; i >= up; i--) {ans[i][left] = element++;}left++;}return ans;}
}

复杂度分析：