[C/C++]数据结构堆的详解-编程知识

一:概念

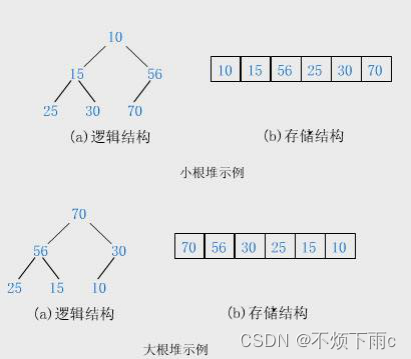
堆通常是一个可以被看做一棵完全二叉树的数组对象,它是一颗完全二叉树,堆存储的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且需要满足每个父亲结点总小于其子节点(或者每个父亲结点总大于其子节点)

堆可以分为两种:

小堆: 任意一个父亲节点都小于其子节点
大堆:任意一个父亲节点都大于其子节点

二:堆的定义

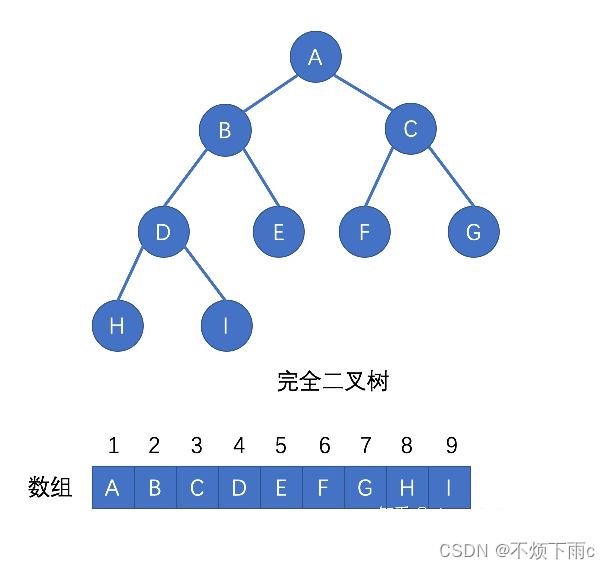
堆是一个完全二叉树,但是其物理逻辑为数组

typedef int HPDataType;
typedef struct heap
{HPDataType* a;int size;      int capacity;  //数组容量
}HP;

接口:

//堆的初始化
void InitHeap(HP* hp);//在堆上入一个数据使其还是堆
void HeapPush(HP* hp, HPDataType x);//在堆上出一个数据使其还是堆
void HeapPop(HP* hp);//取堆头元素
HPDataType HeapTop(HP* hp);//判断堆是否为空
bool HeapEmpty(HP* hp);//求堆的长度
int HeapSize(HP* hp);//堆的销毁
void DestoryHeap(HP* hp);

三:接口实现

堆的实现许多操作和顺序表的实现相同,忘记顺序表的烙铁可以复习一下顺序表-->[C/C++]数据结构----顺序表的实现(增删查改) ,我们以小堆的实现为例:

1.堆的初始化

void InitHeap(HP* hp)
{hp->a = NULL;hp->size = 0;hp->capacity = 0;
}

2.判断堆是否为空

bool HeapEmpty(HP* hp)
{assert(hp);return hp->size == 0;
}

3.堆的销毁

void DestoryHeap(HP* hp)
{assert(hp);free(hp->a);hp->size = 0;hp->capacity = 0;
}

4.返回堆头元素

HPDataType HeapTop(HP* hp)
{assert(hp);assert(hp->size);return hp->a[0];
}

5.堆的大小

int HeapSize(HP* hp)
{assert(hp);return hp->size;
}

到重点啦!!!

ps:下面的向下和向上调整法都是按小堆实现的,若要按大堆实现只需改下大小比较符号即可

6.入堆(在堆里面插入一个数据,使其还是堆)

先将数据插入到堆的末尾,如果堆的性质被破坏的话,就让该节点与其父亲结点交换,向上调整,直到满足堆的性质

例如:在小堆后面插入数据10

由于10小于他的父亲结点,所以应该让10和其父亲结点交换

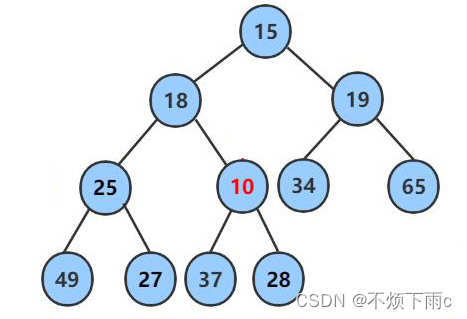
此时10仍然小于其父亲节点,继续交换

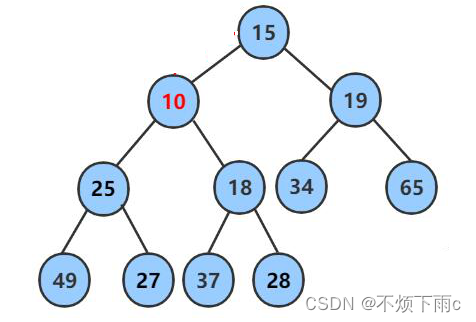
仍然不满足堆的性质,继续交换

向上调整完成

这些数据的存储逻辑上堆为二叉树结构,实际上数据储存在数组中,向上调整法涉及到了如何通过孩子结点找到双亲结点,其实这里有一些结论可以通过一方的下标找到另一方的下标

parent = (child-1)/2
leftchild = parent*2+1
rightchild = parent*2+2

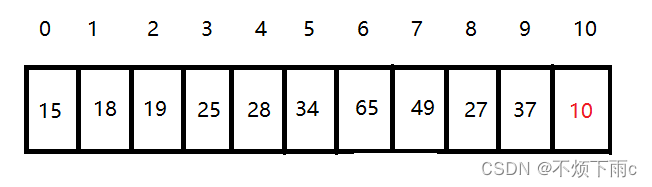
向上调整法代码实现:

void AdjustUP(HP* hp, int child)
{int parent = (child - 1) / 2;while (child > 0) //最坏的情况就是需要调整到下标为0的位置{if (hp->a[parent] > hp->a[child]){swap(&hp->a[parent], &hp->a[child]);child = parent;parent = (parent - 1) / 2;}else{//由于插入数据前本来就是堆,如果不满足上述条件,说明所有数据已经满足堆的性质了break;}}
}

入堆:

void HeapPush(HP* hp, HPDataType x)
{assert(hp);//判断是否需要扩容if (hp->size == hp->capacity){int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* ret = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (ret == NULL){perror("realloc");exit(-1);}hp->a = ret;hp->capacity = newcapacity;}//尾插数据hp->a[hp->size] = x;hp->size++;//向上调整AdjustUP(hp, hp->size - 1);
}

7.堆的删除

堆的删除默认是删除堆顶的元素,如果直接删除堆顶的元素,再将其孩子结点中较小的结点作为堆顶的话,会导致大小关系错乱,因为本来堆顶的左右子树就是堆,按刚刚讲的方法,其堆结构就会被破坏,还需要重新建堆调整,这样的消耗太大了,相反,如果删除一个堆尾的元素消耗却很小,所以可以按如下方法:

把堆顶元素和堆尾元素交换
删除堆尾元素
将堆头元素向下调整到合适位置

向下调整法代码实现:

void AdjustDown(HPDataType* a, int size, int parent)
{//这里假设左孩子是两孩子里面较大的HPDataType child = parent * 2 + 1;while (child<size){    //验证假设是否成立,不成立则更新孩子结点//右边的条件是为了排除数组访问越界的情况,child+1是右孩子下标if (a[child + 1] < a[child] && (child + 1) < size){child = child + 1;}//如果父亲结点比孩子结点大,交换if (a[parent] > a[child]){swap(&a[parent], &a[child]);parent = child;child = child * 2 + 1;}else{break;}}
}

堆得删除:

void HeapPop(HP* hp)
{assert(hp);swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a, hp->size, 0);
}

四:效果展示

heap.h :用于结构的定义和函数的声明


#pragma once	
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;
typedef struct heap
{HPDataType* a;int size;int capacity;
}HP;void InitHeap(HP* hp);
void HeapPush(HP* hp, HPDataType x);
void HeapPop(HP* hp);
HPDataType HeapTop(HP* hp);
bool HeapEmpty(HP* hp);
int HeapSize(HP* hp);
void DestoryHeap(HP* hp);

heap.c: 用于函数的实现

#define  _CRT_SECURE_NO_WARNINGS 1		
#include"heap.h"void InitHeap(HP* hp)
{hp->a = NULL;hp->size = 0;hp->capacity = 0;
}void DestoryHeap(HP* hp)
{assert(hp);free(hp->a);hp->size = 0;hp->capacity = 0;
}void swap(HPDataType* a, HPDataType* b)
{HPDataType tmp = *a;*a = *b;*b = tmp;
}void AdjustUP(HP* hp, int child)
{int parent = (child - 1) / 2;while (child > 0){if (hp->a[parent] > hp->a[child]){swap(&hp->a[parent], &hp->a[child]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HeapPush(HP* hp, HPDataType x)
{assert(hp);if (hp->size == hp->capacity){int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* ret = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (ret == NULL){perror("realloc");exit(-1);}hp->a = ret;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;AdjustUP(hp, hp->size - 1);
}HPDataType HeapTop(HP* hp)
{assert(hp);assert(hp->size);return hp->a[0];
}bool HeapEmpty(HP* hp)
{assert(hp);return hp->size == 0;
}int HeapSize(HP* hp)
{assert(hp);return hp->size;
}void AdjustDown(HPDataType* a, int size, int parent)
{HPDataType child = parent * 2 + 1;while (child<size){if (a[child + 1] < a[child] && (child + 1) < size){child = child + 1;}if (a[parent] > a[child]){swap(&a[parent], &a[child]);parent = child;child = child * 2 + 1;}else{break;}}
}void HeapPop(HP* hp)
{assert(hp);swap(&hp->a[0], &hp->a[hp->size - 1]);hp->size--;AdjustDown(hp->a, hp->size, 0);
}

test.c :测试功能

#define  _CRT_SECURE_NO_WARNINGS 1		
#include"heap.h"
int main()
{int a[] = { 9,8,7,6,5,4,3,2,1 };HP hp;InitHeap(&hp);//这里是将数组的数据依次插入形成堆for (int i = 0; i < sizeof(a) / sizeof(int); i++){HeapPush(&hp, a[i]);}//依次打印堆头元素while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}return 0;
}