今天文章的内容是关于我们如何利用堆的特性对我们的数组进行排序,还有就是我们的TopK的问题,这次我们放在的是文件种,我们放入一亿个数字,然后我们取出一亿个数字中最大的十个数,利用上章堆的问题进行解决。
首先就是我们如果对一个数组要进行排序,这个数组是没有任何规律的,就像下面的这个数组。
int arr[] = { 9,4,3,19,12,13,5,8,9 };
那我们得利用我们堆的特性,因为我们知道堆的特性,首先堆顶的数据一定是最小的,那我们要进行排序之前的话,要做的一个最重要的步骤就是先建立一个堆出来,我们可以用两种方法,一种是向上建堆,另一种就是向下建堆,这两个方法我们都会讲。
向上建堆
首先我们这里给的例子是升序,但是在升序的时候,我们是建立大堆还是小堆呢?答案是
大堆,那我们先来看看减小堆的时候,会产生怎样的问题,再来看看大堆,两者相互比较之后,我们就会发现升序就应该建立大堆。
首先就是复用我们上次堆的内容的向上建堆的那个方法,就是AdjustUp,如果这里大家不明白可以回头看看,我这里直接给出代码。
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
我们可以看到这是向上调整,那我们建堆的过程是不是从二叉树的第二层开始往上建堆,比较的就是孩子和父亲的关系,那我们这里就可以写一个循环来完成这个建立堆的过程。
int arr[] = { 9,4,3,19,12,13,5,8,9 };for (int i = 1; i < sizeof(arr) / sizeof(arr[0]); i++){AdjustUp(arr, i);}
然后我们这个过程建立出来堆的样子就是我们的小堆
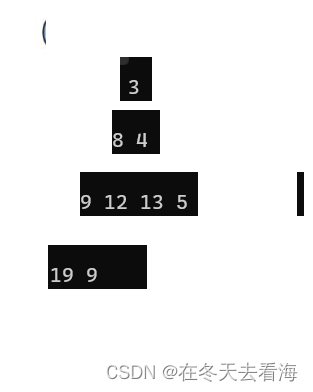
小堆建好之后,我们后面一步就是进行排序,但是排序有个问题,虽然我们保证了一开始堆顶的元素是最下的,但是我们怎么找出第二小,和第三小的数,如果我们这里有人说,我们可以利用堆的向下调整方法,然后重新建立堆,找出次小的,一次这样往下走就没问题,虽然说这样是可以完成排序,但是这样的排序方法甚至比冒泡还慢,看似用了堆的特性,其实时间复杂度比冒泡排序还高,那这样就没能完成我们堆的作用,但是如果我们建立大堆的话,结果·就·有所·不一样,我们可以不找小的,我们先排序后面的。
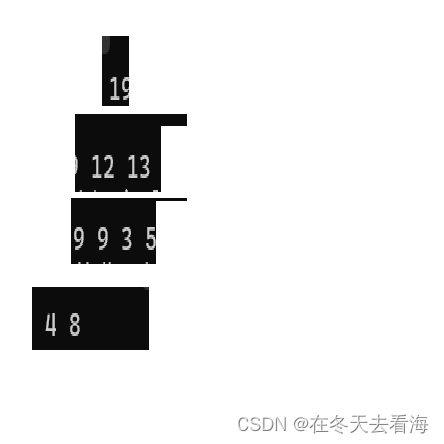
建立大堆后的样子,那我们可以先交换第一个元素和最后一个元素,然后再进行 向下调整,我们后面也会详细计算向下调整和向上调整的时间复杂度的,我们先来看如果交换第一个和最后一个元素的位置,那就变成下面这样。
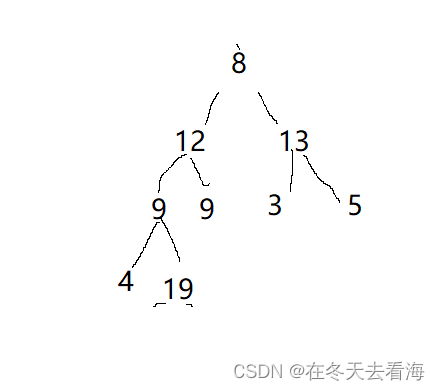
这是进行交换之后的样子,但是还是有问题,我们要保证我们这个还是大堆,那该怎么做呢,首先就是得向下调整,向下调整就是堆顶的元素往下调整,我们利用堆的特性之间写的AdjustDown,调整好之后,是下面的这个图。
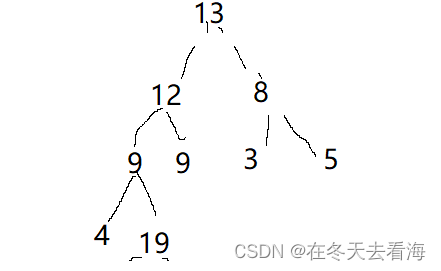
这个时候我们发现最后一个元素是最大的,有序的,而且我们还是大堆,那现在堆顶的元素就是次·大的数,所以现在要做的就是第一个和倒数第二个换位置,然后再进行调整,这样倒数两个的就是有序,有序之后他还是大堆,堆顶的元素就是第三个最大的数,这样一次循环,一直到最后就变成有序了。
那我们的代码就是下面这个,其实代码很简答的主要可能难理解。
AdjustDown
void AdjustDown(int* a, int size, int parent)
{int child = 2 * parent + 1;while (child < size){if (a[child + 1] > a[child] && child+1 < size){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}
这个就是AdjustDown的代码,再堆里讲过,这样就不将了,来看我们如何进行排序的部分代码
int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//这里的end是元素个数,如果是下标的话就是指最后一个元素的后一个end--;}
end = 0的时候就说明已经排序好了,所以这个就是判断条件,然后来看我们的end一开始就是指向最后一个元素,因为是数组,所以这里表示的就是下标,我们这里就是要注意这个,然后先是交换堆顶元素和最后一个元素的问题,就直接开始调整,但是调整的时候我们end并没有进行–,因为
AdjustDown的size位置的参数表示的就是元素个素,然后我们调整的时候因为最后一个元素已经有序了,所以就不用在进行调整了。
我们来看看结果

可以发现我们也是排好序了,这里呢还有要讲一个内容就是建堆,我们那个时候建堆是向上调整,是从第二层开始的,我们也可以用向下建堆的方法,向下建堆要保证两边的子树都是堆,比如我们现在是大堆,所以子数就得是大堆,我们第一次进行调整得应该是第一个父亲节点,我们可以用(size - 1- 1)/ 2找到第一个父亲节点。因为我们堆虽然看起来是个二叉树,但是实际上就是一个数组,我们这里来看代码是如何实现得。
int main()
{int arr[] = { 9,4,3,19,12,13,5,8,9 };int n = sizeof(arr) / sizeof(arr[0]);for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}printf("\n");int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);//这里的end是元素个数,如果是下标的话就是指最后一个元素的后一个end--;}for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){printf("%d ", arr[i]);}return 0;
}
这个就是只用了向下调整进行排序,建堆得方法也是用的向下调整得这个方法,那我们后面得来计算一下向上调整和向下调整得时间复杂度,这里先给出得结论就是向下建堆的方法才是最高效的,我们下面给出一个图来分别计算出他们的时间复杂度。
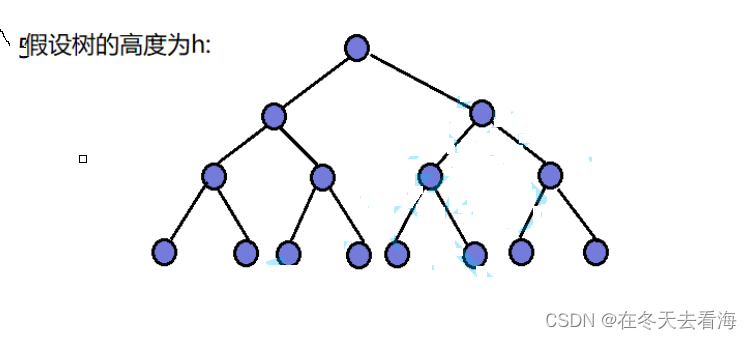
我们给出这样的一个图,首先就是假设这颗数的高度就是H,然后我们在旁边写出他们每一层的节点数。
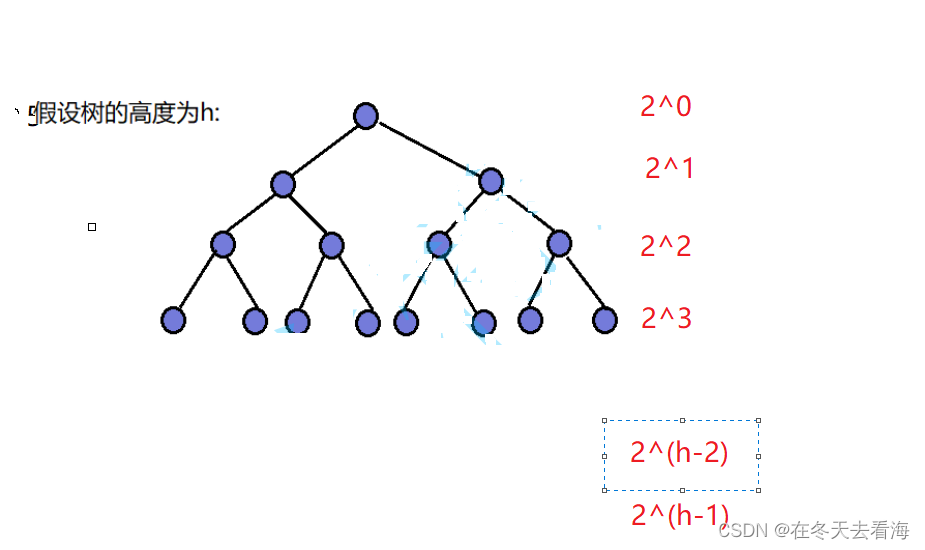
那我们可以再来计算一下他们如果是向上调整的话需要进行的调整次数。
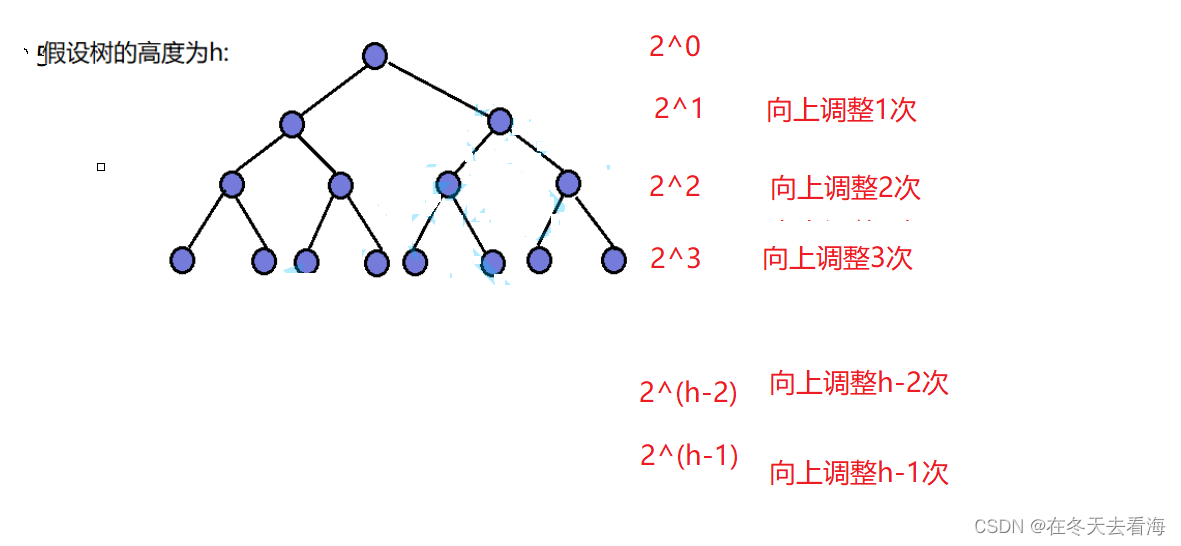
那这个时候我们只要帮他们相乘起来得到一个需要裂项相消的函数。

又因为我们的高度和我们节点个数有个等式,我们就可以把h变成N表示,我们来看看。

这个就是我们向上调整的方式,如果是向下调整的话一样的道理,只是我们是从倒数第二层开始,其实大家自己试试就行了,计算起来是一样的方法,时间复杂度是O(N)我们其实也可以通过分析得出,因为向上调整的方法是和向下的一样的,我这里就讲一个,我们不难看出向上调整的时间复杂度是高于向下的,这是为什么,我们可以看他们最多层,向上调整的时候,我们最多层是最后一层,他的节点数最多,高度也是最高的,所以是多对多,时间复杂度就是要比我们的向下调整,我们向下调整时从最后面的父亲节点开始的,而且只要调整一次就行了,这就是多对少,倒数第二层的节点基本上是整个节点的最后一个,所以我们这里得出的结论就是向下调整是最快的。我们后面就可以直接只用一个向下建堆就可以解决问题了。其实我们这里的排序本质上还是选择排序。
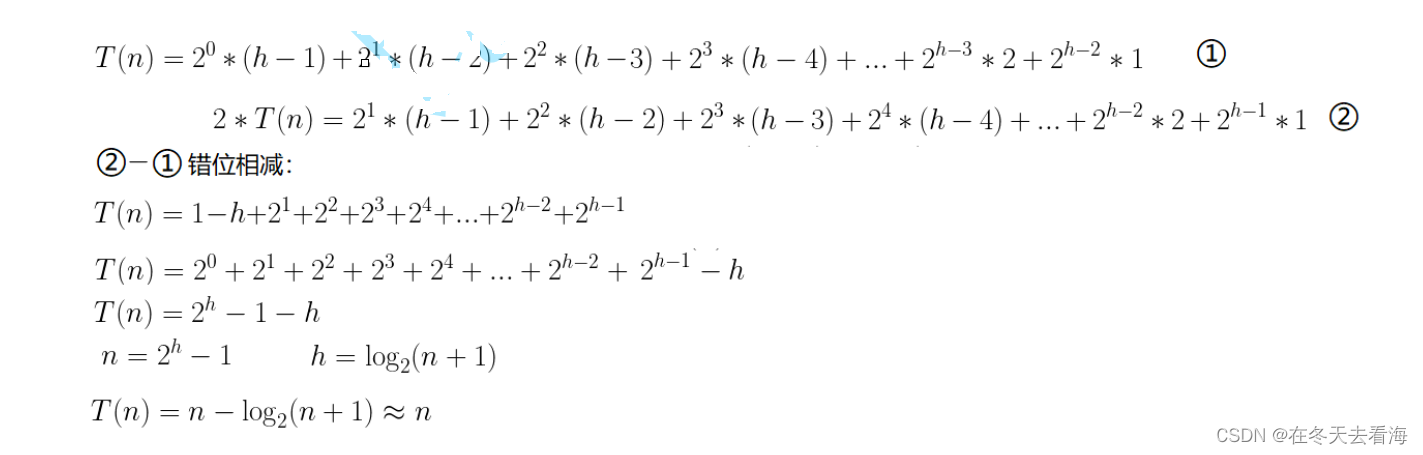
这个是向下建立堆的计算过程,大家可以看看,实在不会就私信小编,谢谢大家。
还有一个TopK问题放在下一篇文章里,因为这样流量多哈哈哈哈哈,下篇文章见。