目录

1、求解问题

2、求解原理

3、python实现

---

1、求解问题

2、求解原理

高斯-勒让德数值积分是一种有效的数值积分方法，它结合了高斯点和勒让德函数来计算一维函数的积分。

高斯-勒让德求积公式在给定的积分区间[a, b]上，通过选择一些特定的点（称为高斯点），并使用与这些点相关的权重系数，来计算积分的近似值。这些高斯点和权重系数是通过将给定的函数展开为勒让德多项式，并使用特定的求积公式来得到的。

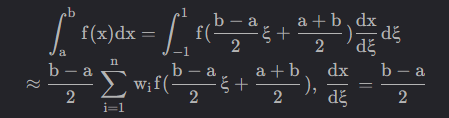
高斯-勒让德求积公式具有很高的精度，特别是对于一些难以使用其他方法积分的函数。它的优点在于，与其他的数值积分方法相比，它通常能够提供更精确的结果，而且对于某些函数，它的计算速度也非常快。

高斯-勒让德数值积分的原理基于高斯积分和勒让德多项式。高斯积分是一种精度很高的插值型数值积分方法，它通过选择一些特定的点（称为高斯点），并使用与这些点相关的权重系数，来计算积分的近似值。勒让德多项式是一类定义在区间[-1, 1]上的多项式，它们可以被展开为无穷级数，也可以被用来近似计算一些函数的积分。

通过将给定的函数展开为勒让德多项式，并使用特定的求积公式，可以将高斯点和权重系数计算出来，从而得到积分的近似值。这种方法适用于各种不同类型的函数，包括多变量函数、三角函数、指数函数等等。

3、python实现

from __future__ import division
import numpy as np
#定义一重积分函数
def gl_quad1d(fun, n, x_lim=None, args=()):if x_lim is None:a, b = -1, 1else:a, b = x_lim[0], x_lim[1]
​if not callable(fun):return (b - a) * fun
​else:loc, w = np.polynomial.legendre.leggauss(n)s = (1 / 2. * (b - a) * fun((b - a) * v / 2. + (a + b) / 2., *args) * w[i]for i, v in enumerate(loc))return sum(s)
​
#定义二重积分函数
def gl_quad2d(fun, n, x_lim=None, y_lim=None, args=()):if x_lim is None:a, b = -1, 1else:a, b = x_lim[0], x_lim[1]if y_lim is None:c, d = -1, 1else:c, d = y_lim[0], y_lim[1]
​if not callable(fun):return (b - a) * (d - c) * funelse:loc, w = np.polynomial.legendre.leggauss(n)s = (1 / 4. * (b - a) * (d - c) * fun(((b - a) * v1 / 2. + (a + b) / 2.,(d - c) * v2 / 2. + (c + d) / 2.), *args) * w[i] * w[j]for i, v1 in enumerate(loc)for j, v2 in enumerate(loc))return sum(s)
​
#定义三重积分函数
def gl_quad3d(fun, n, x_lim=None, y_lim=None, z_lim=None, args=()):if x_lim is None:a, b = -1, 1else:a, b = x_lim[0], x_lim[1]
​if y_lim is None:c, d = -1, 1else:c, d = y_lim[0], y_lim[1]if z_lim is None:e, f = -1, 1else:e, f = z_lim[0], z_lim[1]
​if not callable(fun):return (b - a) * (d - c) * (f - e) * funelse:loc, w = np.polynomial.legendre.leggauss(n)s = (1 / 8. * (b - a) * (d - c) * (f - e) * fun(((b - a) * v1 / 2. + (a + b) / 2.,(d - c) * v2 / 2. + (c + d) / 2.,(f - e) * v3 / 2. + (e + f) / 2.), *args) * w[i] * w[j] * w[k]for i, v1 in enumerate(loc)for j, v2 in enumerate(loc)for k, v3 in enumerate(loc))return sum(s)
​
​
def fun1(x):return 1./(1+x**2)
def fun2(x):return (1+x[0]**2+x[1])**0.5
def fun3(x, a, b):return a * x[0] * x[1] * np.e ** (b * x[2])
​
​
if __name__ == "__main__":res1=gl_quad1d(fun1,5)res2=gl_quad2d(fun2, 3)res3=gl_quad3d(fun3, 3, x_lim=[0,1], y_lim=[-1,0], args=(1,1))print(res1)print(res2)print(res3)
​

1.5711711711711713

4.443748541600919

-0.5875842321700031