数据结构——动态规划

动态规划：有很多重叠子问题，每一个状态一定是由上一个状态推导出来的

贪心：没有状态推导，而是从局部直接选最优的

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

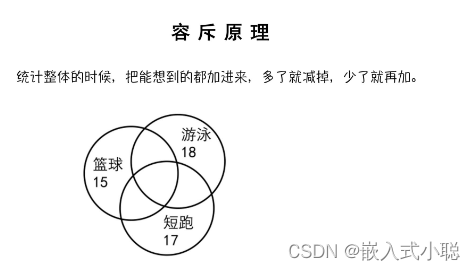
  • 确定递推公式（容斥原理）

  • dp数组如何初始化

  • 确定遍历顺序

  • 举例推导dp数组（用于检验）

一：递推问题

1.1. 如何求解递推问题

正向递推：（递推：一个算法     递归：程序实现的方式，不是算法） 

正向递推（慢）：n-------》1-------》递归

逆向递推（快）：1-------》n-------》循环  

解决效率过差：

1. 递归过程+记忆化

2. 改成逆向递推求解

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

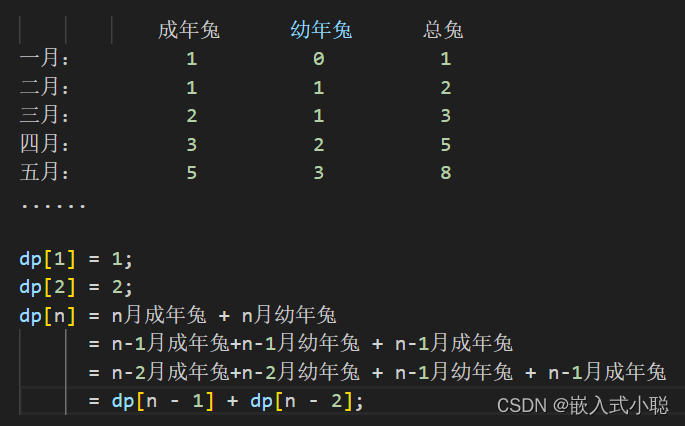
        dp[n]：第n个月的兔子总数是dp[n]

  • 确定递推公式（容斥原理）

        容斥原理 ：dp[n]全集包括：成年兔 + 幼年兔

        dp[n] = dp[n - 1] + dp[n - 2];

  • dp数组如何初始化

        dp[1] = 1;

        dp[2] = 2;

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现：

#include <stdio.h>
#include <stdlib.h>
//正向递推：递归过程+记忆化（提高运行效率）
#define MAX_N 100
int arr[MAX_N + 1] = {0};
int func1(int n) {if (n <= 2) {return n;}if (arr[n]) {return arr[n];}arr[n] = func1(n - 1) + func1(n - 2);return arr[n];
}//逆向递推
int func2(int n) {int *dp = malloc(sizeof(int) * (n + 1));dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}int ret = dp[n];free(dp);return ret;
} int main(int argc, char *argv[]) {int n;scanf("%d", &n);printf("%d\n", func1(n));printf("%d\n", func2(n));return 0;
}

1.2. 容斥原理的基本思想

动规五步曲：

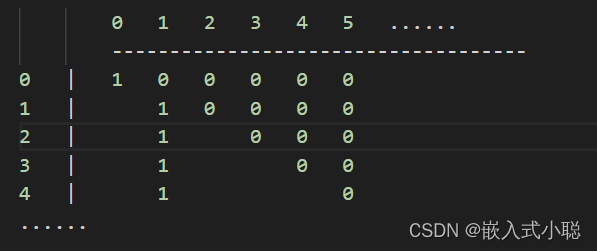
  • 确定dp数组（dp table）以及下标的含义

        dp[i][j]：用前 i 种钱币，凑足 j 元钱的方法总数

  • 确定递推公式（容斥原理）

        容斥原理：dp[i][j]全集包括：没有使用第i种钱币 + 使用第i种钱币

        没有使用第i种钱币：dp[i - 1][j]

        使用第i种钱币：dp[i][j - value[i]]

                                  第一部分：给第i种钱币先留出一个空，用前i种钱币凑够(j - value[i])钱 

                                  第二部分：最后一个空用第i种钱币

        dp[i][j] = dp[i - 1][j] + dp[i][j - value[i]];

  • dp数组如何初始化

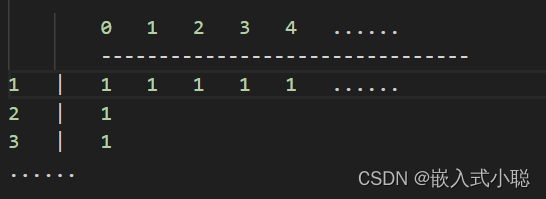
1）

        

        

//初始化
for (int i = 1; i <= m; i++) {dp[i][0] = 1;
}
for (int j = 1; j <= n; j++) {if (w[1] <= j && (j % w[1] == 0)) {dp[1][j] = 1;} else {dp[1][j] = 0;}
}

2）

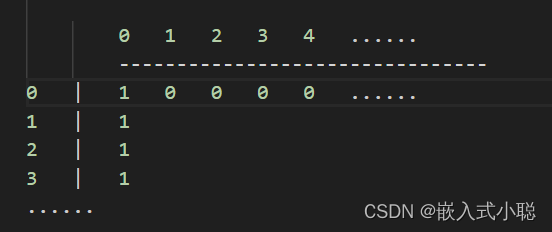
//初始化
memset(dp[0], 0, sizeof(int) * n); //将第0行初始化为0
for (int i = 1; i <= m; i++) {dp[i][0] = 1; //初始化第i行第0列为1
}

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现:

//1)动态规划
#include <stdio.h>
#define MAX_N 10000
#define MAX_M 20
int w[MAX_M + 1];
int dp[MAX_M + 1][MAX_N + 1];int main(int argc, char *argv[]) {int m, n; //m种面额的钱币凑足n元钱scanf("%d%d", &m, &n);for (int i = 1; i <= m; i++) {scanf("%d", w + i);}//初始化for (int i = 1; i <= m; i++) {dp[i][0] = 1;}for (int j = 1; j <= n; j++) {if (w[1] <= j && (j % w[1] == 0)) {dp[1][j] = 1;} else {dp[1][j] = 0;}}for (int i = 2; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j];if (j < w[i]) {continue;}dp[i][j] += dp[i][j - w[i]];dp[i][j] %= 9973;}}printf("%d\n", dp[m][n]);return 0;
}//2)动态规划
#include <stdio.h>
#include <string.h>#define MAX_N 10000
#define MAX_M 20
int w[MAX_M + 5];
int dp[MAX_M + 5][MAX_N + 5];int main(int argc, char *argv[]) {int m, n; //m种面额的钱币凑足n元钱scanf("%d%d", &m, &n);for (int i = 1; i <= m; i++) {scanf("%d", w + i);}memset(dp[0], 0, sizeof(int) * n); //将第0行初始化为0for (int i = 1; i <= m; i++) {dp[i][0] = 1; //初始化第i行第0列为1for (int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j];if (j < w[i]) {continue;}dp[i][j] += dp[i][j - w[i]];dp[i][j] %= 9973;}}printf("%d\n", dp[m][n]);return 0;
}//3)回溯

1.3. 随堂练习1：爬楼梯

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

        dp[n]：走到第n阶台阶的方法总数

  • 确定递推公式（容斥原理）

        容斥原理：dp[n]全集包括：最后跨2步到达第n阶台阶 + 最后跨3步到达第n阶台阶

        dp[n] = dp[n - 2] + dp[n - 3];

  • dp数组如何初始化

        dp[1] = 0;

        dp[2] = 1;

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现：

#include <stdio.h>#define MAX_N 500
int dp[MAX_N + 1];int func(int n) {dp[0] = 1;dp[1] = 0;dp[2] = 1;for (int i = 3; i <= n; i++) {dp[i] = dp[i - 2] + dp[i - 3];}return dp[n];
}int main(int argc, char *argv[]) {int n;scanf("%d", &n);printf("%d\n", func(n));return 0;
}

💖1.4. 随堂练习1：墙壁涂色

   

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

       dp[n][i][j]代表前n块墙壁，在不考虑头尾成环的前提下，第1块涂颜色i，第n块涂颜色j的方法总数

        此时 i 可以等于 j ,最后统计答案时去除相等的情况

  • 确定递推公式（容斥原理）

        容斥原理：dp[n][i][j]全集包括：第1块涂颜色i，第n-1块涂颜色k(k != j)，第n块涂颜色j

        dp[n][i][j] = dp[n-1][i][k]（k != j）的累加

  • dp数组如何初始化

        

        

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

     

二：递推-课后实战题

2.1. 数的划分

动规五步曲：

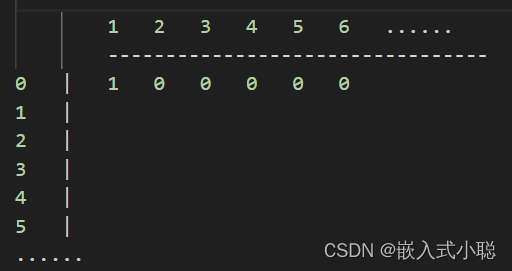
  • 确定dp数组（dp table）以及下标的含义

        dp[i][j]：将数字 i 分成 j 份的方法总数

  • 确定递推公式（容斥原理）

        容斥原理：dp[i][j]全集包括：拆分方案中有1 + 拆分方案中没有1

        拆分方案中有1：留下最后一个位置放1，dp[i - 1][j - 1]

        拆分方案中没有1：将所有方案中的 j 个数都减1，得到另外一个数（i - j）分成 j                                        份的结果，将i - j的所有方案列出来，每个数都加上1，就是拆分方                                         案中没有1的结果，所以拆分方案中没有1的方法总数 == 将数字 i  -                                         j分成 j 份的方法总数 ，即dp[i - j][j]

        dp[i][j] = dp[i - 1][j - 1] + dp[i - j][j];        

  • dp数组如何初始化

        

        

int dp[MAX_N + 1][MAX_K + 1] = {0};
for (int i = 1; i <= n; i++) {dp[i][1] = 1;
}

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现：

//动态规划
#include <stdio.h>#define MAX_N 200
#define MAX_K 6
#define min(a, b) ((a) > (b) ? (b) : (a))int dp[MAX_N + 1][MAX_K + 1] = {0};int main(int argc, char *argv[]) {int n, k;scanf("%d%d", &n, &k);dp[0][0] = 1;for (int i = 1; i <= n; i++) {dp[i][1] = 1;for (int j = 2; j <= min(i, k); j++) {dp[i][j] = dp[i - 1][j - 1] + dp[i - j][j];}}printf("%d\n", dp[n][k]);return 0;
}//回溯

2.2. 数的计算

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

       dp[i]：以i作为开头的合法的数列个数

  • 确定递推公式（容斥原理）

        容斥原理：dp[i]全集包括：

                          以i作为结尾（不扩展）+ i后面接i/2 + i后面接i/2-1 ...... + i后面接1

                                    1                             dp[i/2]          dp[i/2-1]                dp[1]

        dp[i] = dp[j]的累加（j <= i/2）+ 1                                     

  • dp数组如何初始化

        

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现：

#include <stdio.h>#define MAX_N 1000
int dp[MAX_N + 1] = {0};int main(int argc, char *argv[]) {int n;scanf("%d", &n);for (int i = 1; i <= n; i++) {dp[i] = 1;for (int j = 1; j <= i / 2; j++) {dp[i] += dp[j];}}printf("%d\n", dp[n]);return 0;
}

2.3. 神经网络

2.4. 栈

题目描述：1 <= n <=18 的合法出栈序列一共有多少种

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

        dp[n]：1—n的合法出栈序列方案数

  • 确定递推公式（容斥原理）

        容斥原理：dp[n]全集包括：出栈序列末尾是1的方案数 + 出栈序列末尾是2的方案数 + 出栈序列末尾是3的方案数 + ...... + 出栈序列末尾是n的方案数

        小于x的数不断入栈出栈---》x入栈---》大于x的数不断入栈出栈---》x出栈

        第一部分：小于x的数   第二部分：大于x的数   第三部分：x

        所以出栈序列末尾是x的方案数 = dp[x - 1] * dp[n - x]

        dp[n] = dp[x - 1] * dp[n - x]的累加（x == 1; x <= n; x++）

  • dp数组如何初始化

        int dp[MAX_N + 1] = {0};

        dp[0] = 1;

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现：

#include <stdio.h>#define MAX_N 18
int dp[MAX_N + 1] = {0};int main(int argc, char *argv[]) {int n;scanf("%d", &n);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}printf("%d\n", dp[n]);return 0;
}

2.5. 循环

2.6. 传球游戏

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

        dp[j][i]：传了j轮球，球在第i个人手里的方法总数

  • 确定递推公式（容斥原理）

        容斥原理：dp[j][i]全集包括：

                                      倒数第二轮时球在第i-1个人手里 + 倒数第二轮时球在第 i+1个人手里

                                                    dp[j - 1][i - 1]                              dp[j - 1][i + 1]

        dp[j][i] = dp[j - 1][i - 1] + dp[j - 1][i + 1]

  • dp数组如何初始化

        

  • 确定遍历顺序

        从前往后

  • 举例推导dp数组（用于检验）

代码实现：

#include <stdio.h>#define MAX_N 30
#define MAX_M 30
int dp[MAX_N + 1][MAX_N + 1] = {0};int main(int argc, char *argv[]) {int n, m;scanf("%d%d", &n, &m);dp[0][1] = 1;for (int j = 1; j <= m; j++) {for (int i = 2; i <= n - 1; i++) {dp[j][i] = dp[j - 1][i + 1] + dp[j - 1][i - 1];}//单独处理边界dp[j][1] = dp[j - 1][2] + dp[j - 1][n];dp[j][n] = dp[j - 1][1] + dp[j - 1][n - 1];}printf("%d\n", dp[m][1]);return 0;
}

2.7. Hanoi 双塔问题

动规五步曲：

  • 确定dp数组（dp table）以及下标的含义

  • 确定递推公式（容斥原理）

  • dp数组如何初始化

  • 确定遍历顺序

  • 举例推导dp数组（用于检验）

三：动态规划

3.1. 全面剖析：数字三角形问题

1. 斐波那契数

动规五部曲：

1. 确定dp数组以及下标的含义        

         一维dp数组保存递归的结果

        dp[i]的定义为：第i个数的斐波那契数值是dp[i]

2. 确定递推公式

        状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

3. dp数组如何初始化

        dp[0] = 0;
        dp[1] = 1;

4. 确定遍历顺序

        从递归公式dp[i] = dp[i - 1] + dp[i - 2]中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到后遍历的

5. 举例推导dp数组

        按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2]，我们来推导一下，当n为10的时候，dp数组应该是如下的数列：   0 1 1 2 3 5 8 13 21 34 55

代码实现：

//1) 动归第一种解法 时间复杂度：O(n)  空间复杂度：O(n)
int fib(int n) {if (n <= 1) {return n;}int *dp = malloc(sizeof(int) * (n + 1));dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}int ret = dp[n]; //防止内存泄漏free(dp);return ret;
}//2) 动规第二种解法  时间复杂度：O(n)  空间复杂度：O(1)
int fib(int n) {if (n <= 1) {return n;}int dp[2];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {int sum = dp[0] + dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];
}//3) 递归+记忆化解法
#define MAX_N 30
int arr[MAX_N + 1] = {0}; //优化：记忆化(防止大量重复运算，加快运行效率)
int fib(int n) {if (n <= 1) {return n;}if (arr[n]) {return arr[n];}arr[n] = fib(n - 1) + fib(n - 2);return arr[n];
}

2. 爬楼梯

动规五步曲：

1. 确定dp数组以及下标的含义

一维dp数组保存递归的结果

dp[i]：爬到第i层楼梯，有dp[i]种方法

2. 确定递推公式

从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来

首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶就是dp[i]了

还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶就是dp[i]了

那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！

所以dp[i] = dp[i - 1] + dp[i - 2] 

3. dp数组如何初始化

dp[1] = 1

dp[2] = 2

4. 确定遍历顺序

从递推公式dp[i] = dp[i - 1] + dp[i - 2]中可以看出，遍历顺序一定是从前向后遍历的

5. 举例推导dp数组

举例当n为5的时候，dp table（dp数组）应该是这样的

代码实现：

//动规
int climbStairs(int n) {if (n <= 2) {return n;}int dp[3];dp[1] = 1; //上一层台阶dp[2] = 2; //上两层台阶for (int i = 3; i <= n; i++) {int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];
}//递归
#include <stdio.h>
#define MAX_N 45
int arr[MAX_N + 1] = {0}; //记忆化优化
int climbStairs(int n) {if (n <= 2) {return n;}if (arr[n])return arr[n];arr[n] = climbStairs(n - 1) + climbStairs(n - 2);return arr[n];
}

3. 使用最小花费爬楼梯

动规五步曲：

1. 确定dp数组以及下标的含义

使用动态规划，就要有一个数组来记录状态，本题只需要一个一维数组dp[i]就可以了

dp[i]的定义：第i个台阶所花费的最少体力为dp[i]

2. 确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]

那么究竟是选dp[i-1]还是dp[i-2]呢？

一定是选最小的，所以dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];

3. dp数组如何初始化

dp[0] = cost[0];
dp[1] = cost[1];

4. 确定遍历顺序

因为是模拟台阶，而且dp[i]又dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组就可以了

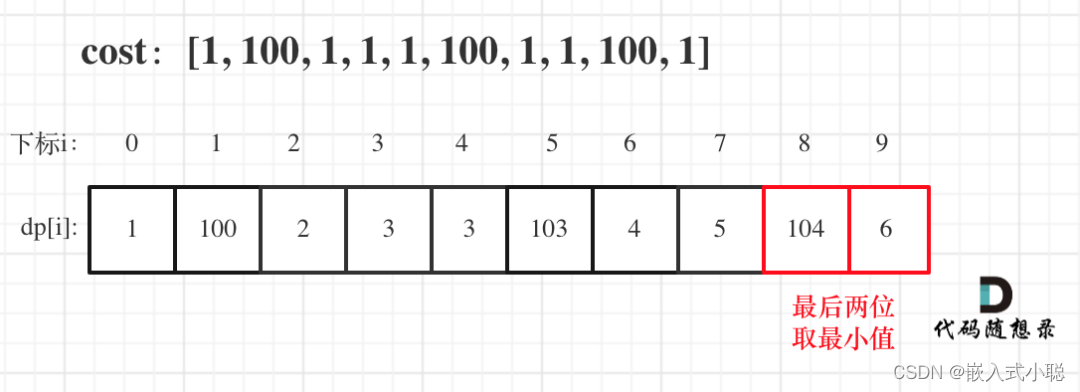
5. 举例推导dp数组

拿示例2：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下dp数组的状态变化，如下：

代码实现：

#define min(a, b)  ((a) > (b) ? (b) : (a))
int minCostClimbingStairs(int* cost, int costSize) {int *dp = malloc(sizeof(int) * (costSize + 1));dp[0] = dp[1] = 0;for (int i = 2; i <= costSize; i++) {dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[costSize];
}

4. 不同路径

动规五步曲：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

2. 确定递推公式

想要求dp[i][j]，只能有两个方向来推导出来，即dp[i - 1][j] 和 dp[i][j - 1]

此时在回顾一下 dp[i - 1][j] 表示啥，是从(0, 0)的位置到(i - 1, j)有几条路径，dp[i][j - 1]同理

那么很自然，dp[i][j] =  dp[i - 1][j] + dp[i][j - 1]，因为dp[i][j]只有这两个方向过来

3. dp数组的初始化

p[i][0]一定都是1，因为从(0, 0)的位置到(i, 0)的路径只有一条，那么dp[0][j]也同理。

for (int i = 0; i < m; i++) {dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {dp[0][j] = 1;
}

4. 确定遍历顺序

递归公式dp[i][j] =  dp[i - 1][j] + dp[i][j - 1]，dp[i][j]都是从其上方和左方推导而来，那么从左到右一层一层遍历就可以了。

5. 举例推导dp数组

代码实现：

int uniquePaths(int m, int n) {//动态创建一个二维路径答案表int **dp = (int **)malloc(sizeof(int *) * m);for (int i = 0; i < m; i++) {dp[i] = (int *)malloc(sizeof(int) * n);}//最左一行for (int i = 0; i < m; i++) { dp[i][0] = 1;}//最上一行for (int j = 0; j < n; j++) {dp[0][j] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];
}

5. 不同路径 II

​

​

动规五步曲：

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径

2. 确定递推公式

dp[i][j] =  dp[i - 1][j] + dp[i][j - 1]

(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）

//当(i, j)没有障碍的时候，再推导dp[i][j]
if (obstacleGrid[i][j] == 0) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}

3. dp数组如何初始化

​

for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {dp[0][j] = 1;
}

4. 确定遍历顺序

从左到右一层一层遍历

5. 举例推导dp数组

拿示例1来举例如题：

​
对应的dp table 如图：

​

代码实现：

6. 整数拆分

​

动规五步曲：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/222994.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【差旅游记】新疆哈密回王府印象

【差旅游记】新疆哈密回王府印象

哈喽&#xff0c;你好啊&#xff0c;我是雷工&#xff01; 2023年11月4号&#xff0c;那天的风的确挺大&#xff0c;逛完哈密博物馆考虑要不要去旁边的哈密回王府逛逛。想着来都来了&#xff0c;虽然网上评价不太好&#xff0c;还是去溜达一圈吧&#xff0c;于是决定自己去转转…
阅读更多...
P20 C++虚函数与纯虚函数

P20 C++虚函数与纯虚函数

目录 前言 01 虚函数能干什么呢? 02 没有虚函数前的例子 03 使用虚函数后的例子 虚函数virtual 概念 虚函数使用需要一定开销 前言 本期我们学习的是 C 中的虚函数。 过去的几期&#xff0c;我们一直在讨论类、面向对象编程、继承这些内容&#xff0c;所有的这些内容&a…
阅读更多...
HarmonyOS应用开发者基础认证【题库答案】

HarmonyOS应用开发者基础认证【题库答案】

HarmonyOS应用开发者高级认证【题库答案】 一、判断 首选项preferences是以Key-Value形式存储数据&#xff0c;其中Key是可以重复。&#xff08;错&#xff09;使用http模块发起网络请求时&#xff0c;必须要使用on(‘headersReceive’&#xff09;订阅请求头&#xff0c;请…
阅读更多...
Python生日蛋糕

Python生日蛋糕

系列文章 序号文章目录直达链接1浪漫520表白代码https://want595.blog.csdn.net/article/details/1306668812满屏表白代码https://want595.blog.csdn.net/article/details/1297945183跳动的爱心https://want595.blog.csdn.net/article/details/1295031234漂浮爱心https://want…
阅读更多...
Linux系统---僵尸进程、孤儿进程

Linux系统---僵尸进程、孤儿进程

顾得泉&#xff1a;个人主页 个人专栏&#xff1a;《Linux操作系统》 《C/C》 键盘敲烂&#xff0c;年薪百万&#xff01; 有了上一篇博客的学习&#xff0c;我们已经简单了解了进程的基础知识&#xff0c;今天我们再来学习两个特殊的进程&#xff0c;僵尸进程和孤儿进程。 …
阅读更多...
电力感知边缘计算技术网关产品设计方案-硬件方案

电力感知边缘计算技术网关产品设计方案-硬件方案

网关硬件架构设计图： 1.配置方案 配置差异 A类网关 B类网关 CPU
阅读更多...
SpringBoot+Redis编写一个抢红包雨的案例。附源码。

SpringBoot+Redis编写一个抢红包雨的案例。附源码。

案例演示 SpringBootRedis编写一个抢红包雨的案例。附源码 1、案例分析&#xff0c;整体方案介绍 预备上线一个红包雨活动。这个红包雨的思路是活动开始前25分钟&#xff0c;在后台创建活动。然后前端用户进入&#xff0c;到点后将设置的金额拆分成多个小红包&#xff0c;开启倒…
阅读更多...
Redis面试题：分片集群相关问题

Redis面试题：分片集群相关问题

目录 面试官&#xff1a;redis的分片集群有什么作用 面试官&#xff1a;Redis分片集群中数据是怎么存储和读取的&#xff1f; 面试官&#xff1a;redis的分片集群有什么作用 候选人&#xff1a;分片集群主要解决的是&#xff0c;海量数据存储的问题&#xff0c;集群中有多个m…
阅读更多...
函数指针数组指针数组传参的本质字符指针

函数指针数组指针数组传参的本质字符指针

&#x1f680; 作者&#xff1a;阿辉不一般 &#x1f680; 你说呢&#xff1a;不服输的你&#xff0c;他们拿什么赢 &#x1f680; 专栏&#xff1a;爱上C语言 &#x1f680;作图工具&#xff1a;draw.io(免费开源的作图网站) 如果觉得文章对你有帮助的话&#xff0c;还请点赞…
阅读更多...
redis报错3

redis报错3

INFO: Initializing SpringDispatcherServletdispatcherServlet
阅读更多...
Linux网络——数据链路层

Linux网络——数据链路层

目录 一.认识以太网 二.以太网帧格式 三.认识MAC地址 四.认识MTU 五.以太局域网的通信原理 六.其他重要协议 1.DNS协议 2.域名简介 3.ICMP协议 4.NAT技术 5.NAT技术的缺陷 6.NAT和代理服务器 一.认识以太网 "以太网" 不是一种具体的网络, 而是一种技术标…
阅读更多...
Redis实战篇（一）短信登录

Redis实战篇（一）短信登录

Redis实战篇&#xff08;一&#xff09;短信登录 1.1、导入黑马点评项目 1.1.1 、导入SQL 1.1.2、有关当前模型 手机或者app端发起请求&#xff0c;请求我们的nginx服务器&#xff0c;nginx基于七层模型走的事HTTP协议&#xff0c;可以实现基于Lua直接绕开tomcat访问redis&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023